摘要：提出了一種基于最優搜索的稀疏傅里葉變換(SFT)的并行實現設計。首先將輸入信號分為并行N組，分別進行快速傅里葉變換(FFT)，實現信號頻率分量的取模處理，然后通過排序搜索獲得。經驗證，相較于FFTW，當信號長度大于524 288時，執行時間會有更好的表現；相較于正交匹配算法及其他SFT的FPGA實現，其系統的復雜度降低了。
?

0引言

稀疏傅里葉變換（Sparse Fourier Transform, SFT）是一種新的算法框架，也是快速傅里葉變換（Fast Fourier Transform，FFT）在處理稀疏頻譜信號上的延伸。2003年AYDINER A A等人提出了針對頻域稀疏信號的傅里葉變換基本思想［1］。對于頻域稀疏信號來說，其頻譜可以通過其多級子集頻譜獲得。之后，IWEN M A等人從壓縮感知得到啟發，將采樣和頻率估計整合到快速傅里葉變換并提出了經典SFT框架［2］。之后SFT廣泛運用于稀疏頻譜信號（諸如音頻信號、醫學圖像信號）的處理以及頻譜感知領域［3］。大量的SFT算法被提出，它們多利用經典的頻率估計算法通過亞奈奎斯特采樣點的子集的傅立葉變換重構稀疏頻點［4］。但由于經典SFT的亞奈奎斯特率樣本是通過多次采樣獲得的，因此，經典SFT 不可能代替 FFT來處理實時信號，比如雷達信號等。

2010年以來，一種并行結構的SFT算法受到了廣泛的關注［5］。并行SFT首先通過并行下采樣，采集計算所需的所有時域數據，然后再通過FFT，通過亞線性頻譜估計方法獲得信號的稀疏頻率及其幅值。由于該類方法以并行取代迭代獲得頻譜估計所需的所有信息，因此可以實時處理各種頻域稀疏信號，使得經典SFT得到了改善。基于此，參考文獻［6］~［8］探討了稀疏傅里葉變換在GPU以及多核CPU上的實現方式。這些研究顯示，基于GPU加速的實現方案運行速度要顯著高于基于CPU的實現方案。然而，基于GPU的實現方案都存在主存儲區與GPU存儲區的連接交互問題，因此數據間的正常流動不能得到更好的促進。

為解決GPU的數據并行處理的局限性，本文研究SFT的并行算法并在FPGA上對其進行實現，同時應用中國余數定理（CRT）的基本原理對信號進行重構。相較于傳統的SFT，本文的方法可以極大地降低系統的復雜度，減少了硬件的開銷。本文，首先介紹SFT的并行框架，然后討論SFT的FPGA實現架構，最后從仿真結果以及硬件實現兩方面對系統進行評估。

1SFT并行算法

SFT并行算法主要由下采樣、頻率估計、幅度估計三個部分組成。在下采樣過程中，將輸信號劃分為N個組，每個組的采樣因子分別為σ1,σ2,…,σN。利用中國余數定理（Chinese Residue Theorem，CRT）進行頻率以及幅度的估計，設定各組的采樣因子兩兩互質。

并行SFT算法從L個采樣樣點中重構2 K算個參數，其中包括K個時延參數以及K個幅度參數。重構法的具體計算步驟如下：首先，設采樣通道數為N，每個通道的采樣點數分別為qi,i=1,2,…,N。計算X~=M*X，其中M為下采樣矩陣，X為采樣樣本。之后，對X~進行DFT變換，得到X^=DFT(X~)。按幅度從大到小對X^向量中的值進行排序，計算hk：

hk=kthMAX|X^j|,k∈［0，K］（1）

其中K為指定的重構信號的參數。得到hk之后則可通過求余運算獲取余數信息r1,khk的位置modq1。通過并行查詢的方式搜索余數的最優解：

tminmint∈［0，qj］|hk-X^t*q1+r1,k|,j∈［2，N］（2）

rj,k=r1,k+tmin*q1modqj,j∈［2，N］（3）

利用CRT通過r1,b,…，rN，b重構時延參數τk，幅度估計參數可由公式（4）和 （5）得出：

x=real(hk)|τk

y=imag(hk)|τk(4)

ak=|x+iy|（5）

2SFT主要部分的FPGA實現

本文考慮使用MATLAB Simulink工具構建SFT采樣算法的FPGA實現架構。圖1展示了當采樣通道數N=3時的SFT并行結構，其主要包括下采樣、頻率估計、幅度估計三個部分。　

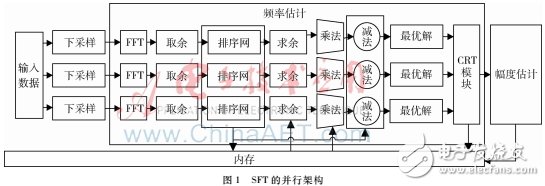
如圖1所示，頻率估計與幅度估計共用部分相同的硬件結構，信號在經過下采樣之后，通過FFT運算得到復數的輸出信號，為了對該復數信號進行排序，將該復數信號取模后送入排序網絡，由于每個通道送入排序網絡的點數不同，排序網絡的結構會稍有差異。在利用CRT估計信號的幅度和頻率之前，需要對信號進行求余、求最優解等運算。其中，最優解運算的核心是排序網絡，利用排序網絡的思想求取輸入信號的最大值以及獲取排序后的信號在原輸入信號中的位置；CRT模塊由一些加法器和乘法器組成。

輸入信號經過多路選擇器獲得下采樣信號，所以該部分主要研究下采樣信號的頻率估計以及幅度估計，頻率估計包括最優解模塊以及CRT重構模塊。另外，硬件構成部門還包含了存儲和控制單元，各通道采樣因子數ql、參數t、排序位置信息等都在存儲單元中保存，控制單元產生地址值來執行讀寫存儲器的操作，并輸出必要的控制信號來初始化運算模塊。

在本設計中，設定信號長度N=223，參數個數K，采樣通道數M=3，其中，各個通道的采樣點分別為q1，q2，q3；q1,q2,q3兩兩互質且乘積大于信號長度N，因此，通過中國余數定理可由q1+q2+q3個采樣點數獲取原始信號所有的信息，降低了幅度以及頻率估計時所需的采樣點數。下面介紹各個主要功能模塊的設計。

2.1頻率估計

2.1.1最優解模塊實現架構

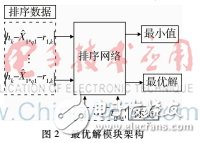
頻率估計模塊的核心部分在于最優解的獲得，最優解實現架構如圖2所示。圖中X^t*q1+r1,k可由采樣樣本經過多路選擇器MUX獲得，根據t的取值不同，可以得到多個定點采樣的樣點值。當排序網絡為三輸入結構時，r1,k代表排序網圖2最優解模塊架構絡模塊中獲得的k1,1,k1,2,k1,3對應位置信息數據對q1取余所得的值。t的取值范圍為0~qj,j=2,3，其中當j=2時，q2=4，同樣地，有q3=5；兩種情況下只有t值的變化導致定點采樣的樣點值的變化，而其對應的模塊架構是相同的，所以這里僅對j=2時的情況加以分析。

根據排序網絡結構，需要的輸入數據有兩組，一組為需要排序的數據，以便求得最小值，另外一組則為數據對應的位置信息t。這樣在排序網絡求取完最小值后可以直接獲取相應的t值而不需要進行其他的運算處理。為此，將需要排序的數據并行導入排序網絡的數據輸入接口，將對應的位置信息t值也并行導入排序網絡的位置信息接口。

如圖3所示，原有輸入的3路信號序號為1,2,3。該模塊實現對這3路信號進行從大到小的排序，并獲得排序后的信號在原序列中的序號，即取位。圖3顯示了3輸入結構的排序圖，4輸入乃至更多輸入結構圖原理相同，圖中比較器的輸出作為多路選擇器的sel選擇端輸入，利用比較器以及多路選擇器的硬件電路連接實現邏輯上的比較選擇排序。k1,1,k1,2,k1,3為3輸入信號經過排序網絡的輸出信號，有k1,1>k1,2>k1,3。k1,1_loc,k1,2_loc,k1,3_loc分別記錄了k1,1,k1,2,k1,3在原序列中的位置。同時將位置信息存儲到位置信息存儲器中。

2.1.2CRT模塊架構

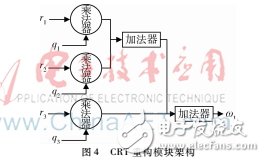
最優解模塊輸出一組余數信息的集合，利用中國余數定理可以輕易地通過一組累加求和運算獲取頻率集合，進一步便可獲取時延參數τk。由中國余數定理可以得到如下方程組：

x≡r1(modq1)

x≡r2(modq2)



x≡rn(modqn) （6）

其中ri（i=1,2,…,n）為頻率點的集合，qi（i=1,2,…,n）為采樣點數的集合。假設Q為q1到qn的乘積，并設Qi=Q/qi,i∈{1,2,…,n}，ti為Qi模qi的數論倒數，則有：

x=∑ni=1ritiQi（7）

圖4顯示了一個頻率點的CRT重構模塊架構。

2.2幅度估計

幅度估計中，利用CRT重構模塊中獲取的頻率集合w1,w2分別與L1,L2作求余運算，以此為基礎求得hk,利用前面式（4）和式（5）可求得原始信號的幅度估計。其中頻率集合w1,w2由CRT模塊獲得，圖5中求余的作用為頻率集合w1,w2分別對采樣點數L1,L2作求余運算。輸入序列xl、稀疏度值、采樣通道數、每個通道的采樣點數存儲在寄存器中供乘法器調用。利用排序網絡分別求得輸入信號實部與虛部的最大值，再對其進行取模則可得到幅度值的估計。幅度估計的模型如圖5所示，其中，排序網絡為4輸入結構。

3結果分析以及性能評估

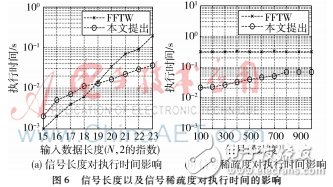
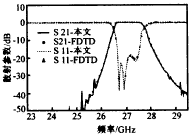
為評估該算法框架的有效性，將其與FFTW做對比，FFTW是一個快速計算離散傅里葉變換的庫,這個庫可以在多核CPU以及GPU上運行。分別考慮稀疏度k恒定為1 000時信號長度的變化對執行時間的影響，以及信號長度N恒定為223時稀疏度的變化對執行時間的影響，比較結果如圖6所示。

將本文討論的稀疏傅里葉變換采樣框架與已知的OMP算法框架作性能上的對比，實現了信號長度N=32，參數個數K=2以及采樣點數的采樣框架。其中，使用RAM塊實現所有所需的向量、常數或矩陣的存儲。將OMP架構［9］以及SFT架構［10］在同樣的平臺下做了實現來與本文算法架構進行對比，其結果如表1所示。

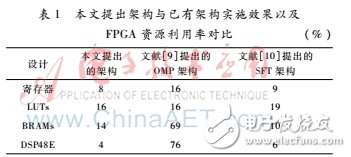
相較于OMP架構，本文提出架構大大減少了DSP48E以及所需寄存器的數量。相較于文獻［10］提出的SFT架構，本文架構依舊能夠有良好的表現。

4結論

本文提出了SFT的FPGA并行實現方案，使用Simulink中的XSG開發工具構建FPGA實現框架。對獨立功能塊的并行化處理可以大大減少執行時間。之后對FPGA上的硬件實現進行了評估，相對于FFTW的實現方案，在采樣點數的量級足夠大時，提高了系統運行速度，降低了計算所需的時間；相對于其他OMP等算法的FPGA實現方案，減少了資源的消耗，降低了系統的復雜度。