1.FFT變換的基本原理
傅立葉變換是數字信號處理領域一種很重要的算法,可以將一個信號從時域變換到頻域。傅立葉原理表明:任何連續測量的時序或信號,都可以表示為不同頻率的正弦波信號的無限疊加。
根據原信號的不同類型,傅里葉變換可以分為四種類別:
(1)非周期性連續信號傅里葉變換
(2)周期性連續信號傅里葉級數
(3)非周期性離散信號離散時域傅里葉變換
(4)周期性離散信號離散傅里葉變換
快速傅里葉變換(FFT),是利用計算機計算離散傅里葉變換(DFT)的高效、快速計算方法的統稱,但是它是基于復數的,復數DFT寫成如下極坐標形式:

在復數傅里葉變換中,x[n]和X[k]都是復數數組,它包括正頻率和負頻率。K從0到N-1,0~N/2的頻率為正值,N/2~N-1為負值。因為離散信號的頻譜是周期性的,其周期等于抽樣頻率。所以N/2到N-1的頻率和-N/2~0的頻率是相同的。0點和N/2點的頻率值為正負頻率的分界。
我們設變換長度N = 2L,將x(n)按照n的奇偶分為兩組
x1(r) = x(2r)
x2(r)= x(2r+1)
其中r=0,1,…,N/2-1,帶入上述復數DFT變換的公式,得到X[k]:
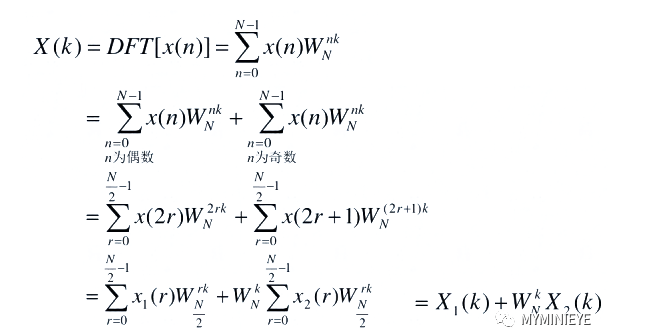
在式子中X1(K)和X2(K)分別是x1(n)和x2(n)的N/2點DFT,因此它只能算出前一半的值,后一半利用
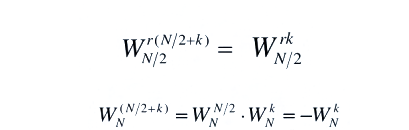
可以得到后半部分X(k)
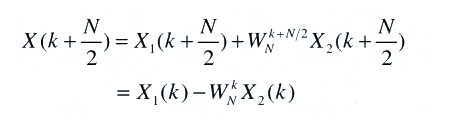
把x(n)的N點DFT合到一起,就是如下的蝶形運算,也是FFT的基本運算單元。
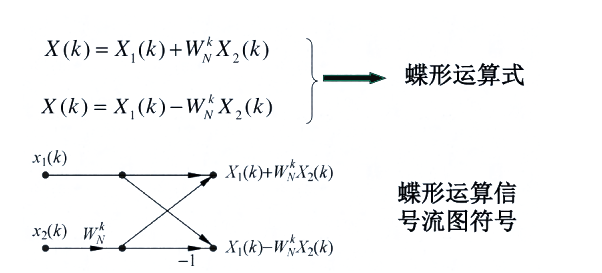
我們以8點的信號為例,三次按照奇偶分解,它的FFT信號流圖如下:
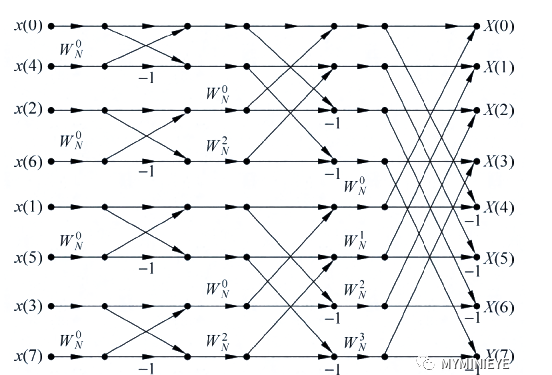
2.抽樣定理
抽樣定理表明:如果一個連續信號f(t),其最高截止頻率為fm,如果用時間間隔為T≤1/(2*fm)的開關信號對f(t)進行時域抽樣,則f(t)可以被樣值信號唯一表示。即保證抽樣頻率fs≥2*fm,可以由抽樣信號fs(t),恢復出原始信號f(t)。
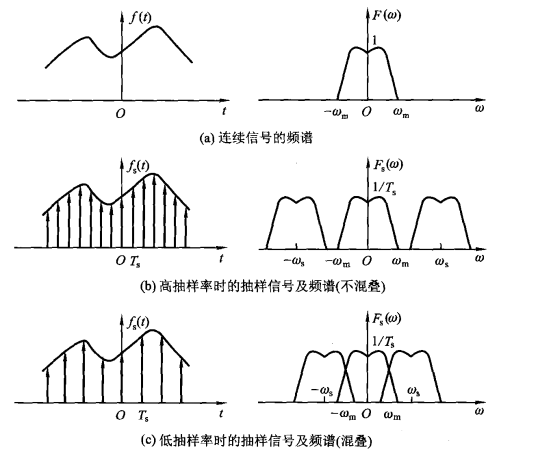
通常把最低允許的抽樣頻率fs=2*fm稱為“奈奎斯特頻率”,把最大允許的抽樣間隔Ts=1/(2*fm)稱為“奈奎斯特間隔”。
3.FFT頻譜分析
因為FFT是基于復數的,在計算FFT的時候會出現兩種情況,輸入的數據為實數和復數,實際當中輸入信號x(n)一般都為實信號,即虛部為零。
(1)輸入數據是實數
我們用matlab產生一個實正弦信號,如下:

正弦信號sin_data包含兩個頻點信號,f1=50Hz,f2=200Hz,采樣頻率fs=1024Hz,采樣點數NFFT=1024,FFT之后結果為一個N點復數。每一個點對應著一個頻率點,這個點的模值,就是該頻率值下的幅度特性。所達到的頻率分辨率為fd=fs/N=1024/1024=1Hz,某一點n所表示的頻率為Fn=(n-1)*fs/N=n-1,每個點的模值是A的N/2倍,其中A為原始信號的峰值。FFT結果如下:
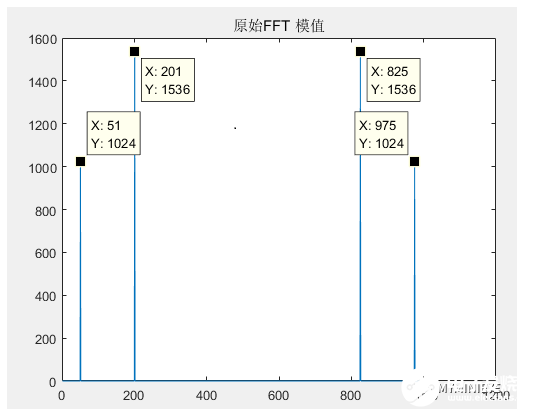
在頻譜圖中,前N/2個點有兩個峰值,后N/2有兩個峰值,是對稱的。在上述中提到,FFT包含周期為2*pi的特性,在做FFT的時候得到的是[0,2*pi],包含一個完整的區間。正頻率分布在[0,N/2]與[0,2*pi]對應,N/2+1是正負頻率的分界點,表示的頻率為奈奎斯特采樣頻率的半,負頻率分布在[N/2+1,N-1]與[pi,2*pi]相對應,[pi,2*pi]就等同于[-pi,0],負頻率沒有物理意義,把上述頻譜圖做調整之后如下:
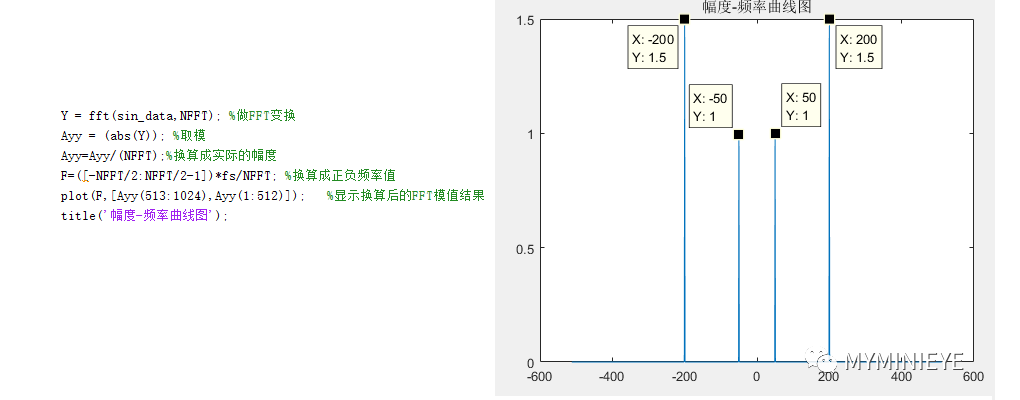
在做實數FFT時,往往將0~N/2點的值作為實際的頻譜,由于正負頻率幅值分量各占一半,幅值需要擴大2倍。
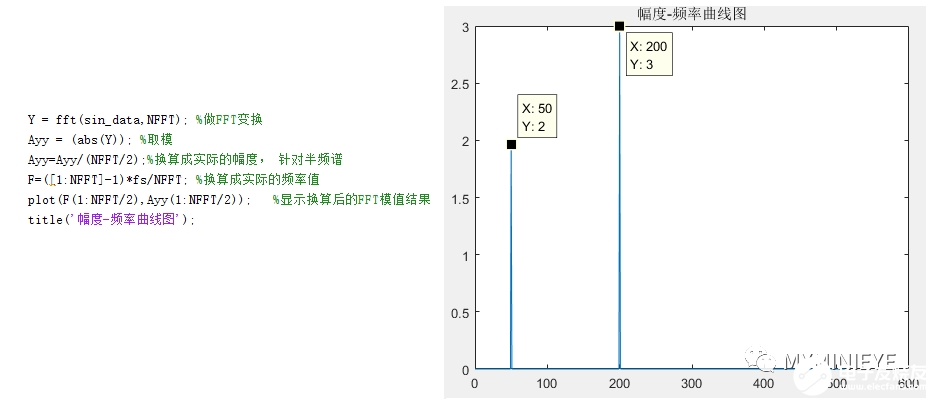
(2)輸入數據是復數
我們用matlab產生一個和上述信號一樣頻率的復數信號,并觀察其FFT之后的頻譜,如下所示:
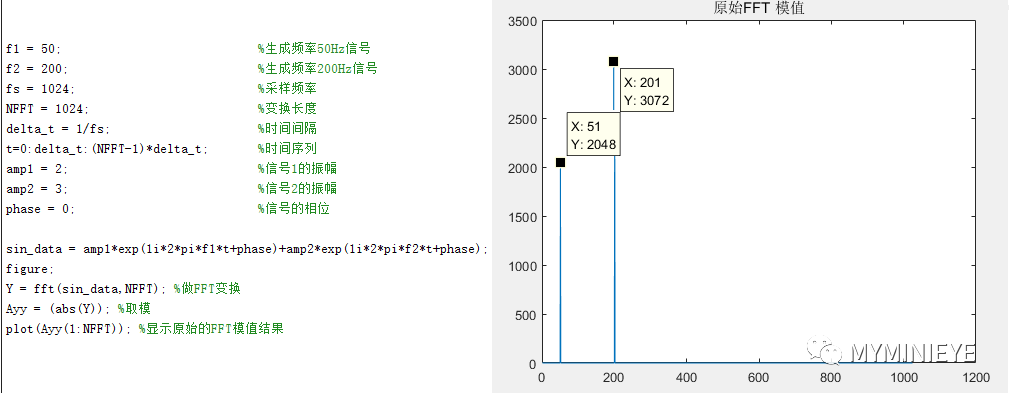
在做復數FFT的時候,只會有兩個峰值,對應兩個頻率,且每個點的模值是A的N倍,A為原始信號的峰值。其實當我們輸入指數形式的信號時,它包含實部和虛部兩個信號,即x(n)=cos(n)+j*sin(n)。相當于是兩個頻譜的疊加,cos(n)產生一個頻譜,j*sin(n)產生一個頻譜,二者相互疊加,并不是沒有了負頻率,而是負頻率相互抵消,正頻率的幅值擴大了二倍。
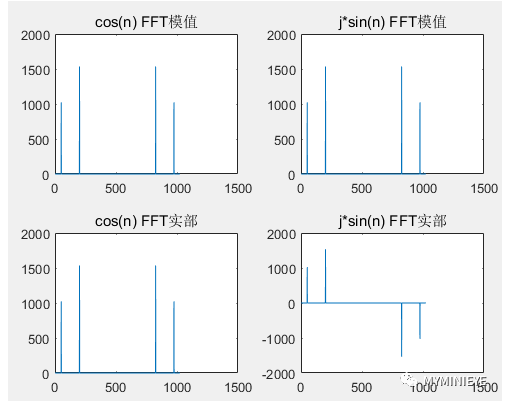
(3)在實際中,通過FFT計算得到頻點信息往往和信號的頻點信息不相同,會有誤差,這就取決于頻譜的分辨率,例如:當fs=1000Hz的時候fd=fs/N=1000/1024=0.97Hz,因為f1=50Hz,f2=200Hz不是fd的整數倍,所以FFT的頻譜中不包含這兩個頻點,只有其周圍相接近的整數倍頻點,通過FFT得到的頻譜如下:
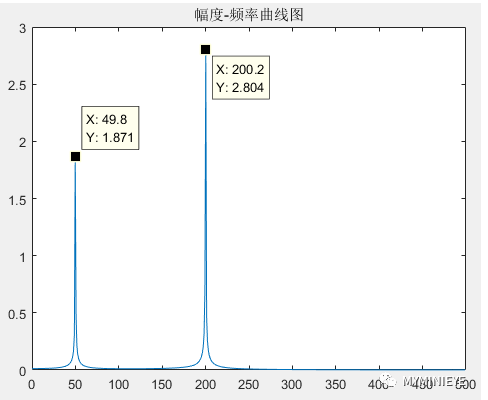
4.頻率分辨率
頻率分辨率也叫做兩個相鄰譜峰分開的能力,指分辨兩個不同頻率信號的最小間隔。我們用matlab產生一個余弦波信號(頻率分別為1MHz和1.05MHz),幅值都為1,采樣頻率fs=100MHz,采樣點數N=1000,對這1000個數據點做FFT得到頻譜如下:
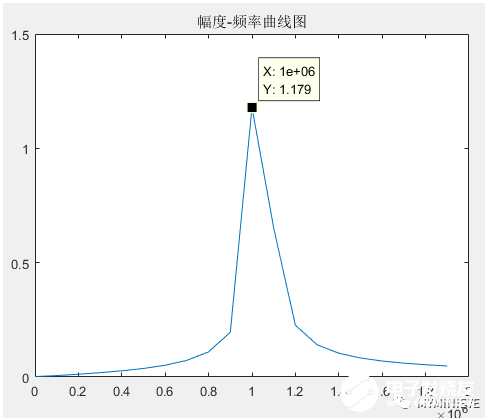
可以發現頻譜點稀疏,在1MHz附近無法將1MHz和1.05 MHz的兩個頻率分開,頻率成分無法被區分,一般由于頻率分辨率不夠造成的。
頻率分辨率大致有兩種類型,一種叫波形分辨率,由原始數據的時間長度決定:
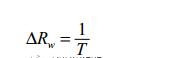
另一種叫視覺分辨率或FFT分辨率,由采樣頻率和參與FFT的數據點數決定:
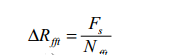
區分不同頻率成分,是為了在數據點數不是以2為基數的整數次方是對原始數據進行“補零”操作。如果直接對原始數據做FFT,這兩種頻率分辨率是相等的。
(1)補零
現在對原始數據進行“補零”操作,在采樣點1000個原始數據后面補充零達到7000個數據點,再對其做FFT,結果如下圖所示:
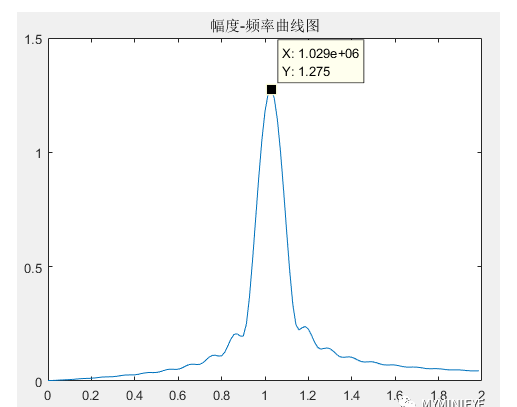
可以發現頻譜點密集了很多,但是在1MHz附近仍無法將兩個頻率成分分開,所以,雖然我們補了很多的零,但是波形分辨率仍然為1/T1 = 100kHz,大于1MHz和1.05MHz這兩個頻率成分之間的距離50kHz。時域補零相當于頻域插值,也就是說,補零操作增加了頻域的插值點數,使得頻域曲線看起來更加光滑,增加了FFT頻率分辨率。
(2)增加數據時間長度
在采樣頻率不變的情況下,想要分辨這兩個頻率,必須要改變波形的分辨率,也就是延長原始數據的時間長度,現在我們以同樣的采樣頻率對信號采7000個點作為原始信號,然后對齊做FFT,得到的結果如下:
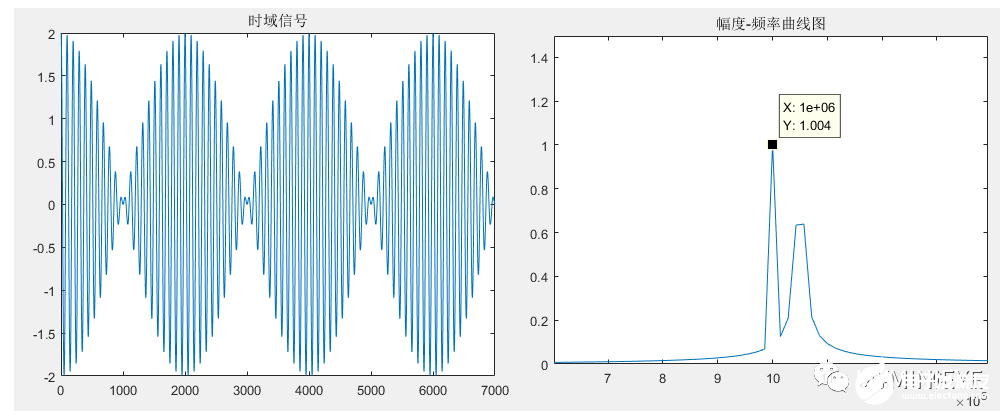
此時的波形分辨率為1/T2=14kHz,小于50KHz,可以看到有兩個明顯的峰值,但是會發現1MHz對應的幅值為1,與原信號中該頻率成分的幅值一致,但1.05MHz對應的幅值明顯低于1,這就是所謂的頻譜泄露。使得在1MHz處有譜線存在,在1.05MHz處沒有譜線存在,使測量結果偏離實際值,同時在實際頻率點的能量分散到其它頻率點上。
(3)為了解決這個問題,我們可以設法使得譜線同時經過1MHz和1.05MHz這兩個頻點,找到他們的最大公約數50kHz,用FFT分辨率計算得到FFT數據點數2000,但是我們的數據點已經有7000了,我們對點數擴大四倍到8000點,也就是補1000個零。這時FFT分辨率為12.5kHz,所以譜線同時經過1MHz和1.05MHz這兩個頻率點,對其做FFT結果如下:
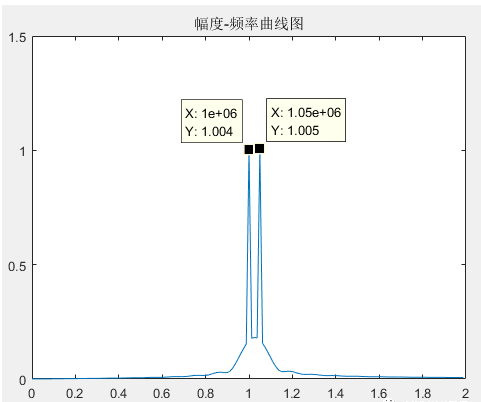
從上圖中可以看到,兩個頻點的幅值均與原信號一致,這也是補零操作帶來的影響。
-
FFT
+關注
關注
15文章
443瀏覽量
60541 -
傅里葉變換
+關注
關注
6文章
442瀏覽量
43013
發布評論請先 登錄
泰克TBS1102X示波器FFT功能使用指南





 為什么使用傅里葉變換 FFT變換的基本原理
為什么使用傅里葉變換 FFT變換的基本原理










評論