有了“1”,還要有“0”才能構成世界,那么頻域的“0”是什么呢?cos(0t)就是一個周期無限長的正弦波,也就是一條直線!所以在頻域,0頻率也被稱為直流分量,在傅里葉級數的疊加中,它僅僅影響全部波形相對于數軸整體向上或是向下而不改變波的形狀。
2023-10-17 15:17:53 119
119 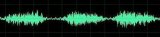
提到傅里葉變換,你是不是又想起了大學課程里被它支配的恐懼。其實,傅里葉分析不僅僅是一個數學工具,更是一種可以徹底顛覆一個人以前世界觀的思維模式。如果用方程寫一部科學史,傅里葉變換必然擁有位置,它
2023-09-11 11:21:06 289
289 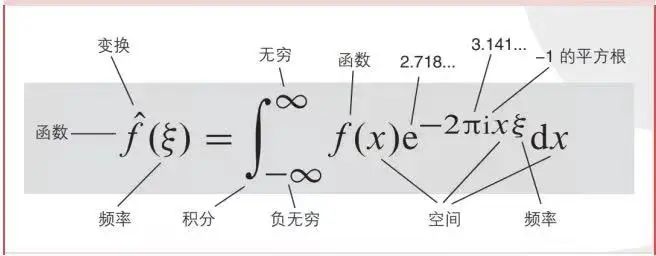
傅里葉變換和離散傅里葉變換的關系 傅里葉變換(Fourier Transform)是一種將時間域(或空間域)的信號轉換為頻率域(或波數域)的信號的數學工具。而離散傅里葉變換(Discrete
2023-09-07 17:04:15 330
330 如何由傅里葉變換推出傅里葉反變換? 傅里葉變換和傅里葉反變換是信號處理和通信領域中的兩個重要概念,是數字信號和連續信號的重要數學分析方法之一。傅里葉變換可以將時間域信號轉化為頻率域信號,而傅里葉反
2023-09-07 17:04:09 356
356 可以表示原始函數中不同頻率的振幅和相位信息。傅里葉變換可以應用于信號處理、通信、圖像處理、量子力學等領域。本文對傅里葉變換中的一些重要公式進行總結和詳細說明。 1. 傅里葉級數公式 傅里葉級數是傅里葉變換的前身,它適
2023-09-07 16:53:08 3859
3859 傅里葉變換和反變換公式? 傅里葉變換和反變換在信號處理領域中被廣泛應用。傅里葉變換是將一個時域信號轉換為頻域信號的過程,而傅里葉反變換則是將一個頻域信號轉換為時域信號的過程。這篇文章將詳細講解
2023-09-07 16:53:04 2916
2916 傅里葉級數展開的求解方法 傅里葉級數展開是一種將周期函數分解為一系列正弦或余弦函數的方法。該方法在數學、物理、信號處理、圖像處理和工程等領域中得到廣泛應用。本文將探討傅里葉級數展開的定義、求解方法
2023-09-07 16:47:58 603
603 傅里葉級數有時移特性 傅里葉級數是指將周期函數分解為一系列正弦函數和余弦函數的和的表達式。它得名于法國數學家傅里葉,被廣泛應用于信號處理、圖像處理、噪聲分析等領域。傅里葉級數的最重要的特征之一
2023-09-07 16:43:50 309
309 傅里葉變換和傅里葉逆變換的關系? 傅里葉變換和傅里葉逆變換是信號處理領域中極具重要性的數學工具,它們被廣泛應用于很多領域,例如音頻、圖像處理、通信等。 傅里葉變換是將一個信號在時域(即時間或空間)上
2023-09-07 16:43:47 581
581 三角級數和傅里葉級數的區別? 三角級數和傅里葉級數是數學中兩個重要的概念。它們都涉及到無窮級數,但它們的應用和本質有所不同。在本文中,我們將深入探討這兩個概念的區別和應用,希望能夠幫助讀者更好地理
2023-09-07 16:43:42 283
283 傅里葉變換和傅里葉級數的關系? 傅里葉變換和傅里葉級數都是數學領域中非常重要的概念和理論,這兩者之間存在著密不可分的聯系。在本文中,我們將從多個角度來深入探討傅里葉變換和傅里葉級數的關系,以便更好
2023-09-07 16:39:01 960
960 正弦函數的傅里葉變換 正弦函數是數學中一種廣泛應用的基本函數,其在傅里葉分析中也是具有重要作用的函數之一。在實際應用中,我們常常需要將正弦函數進行傅里葉變換,以求得自變量函數在頻域上的表現,從而更好
2023-09-07 16:35:07 836
836 傅氏變換和傅里葉變換的區別聯系 傅氏變換和傅里葉變換是信號處理中常用的兩種變換方法,它們有著不同的作用和特點。傅氏變換主要應用于連續時間信號的頻域分析,而傅里葉變換則主要用于離散時間信號的頻域分析
2023-09-07 16:35:05 195
195 傅里葉變換的意義和性質 為什么萬物皆可傅里葉? 傅里葉變換是一種通過將時間域上的函數轉換為頻率域上的函數,來分析信號的方法。它是在18世紀末由法國數學家約瑟夫·傅里葉所發明的,它的形式為一個積分
2023-09-07 16:19:02 385
385 傅里葉變換的數學意義 傅里葉變換是一種數學工具,它是一種將一個函數在一個頻域轉換為另一個函數在另一個頻域中的操作。傅里葉變換起源于1807年,由法國數學家讓·巴蒂斯特·約瑟夫·傅里葉提出,它是一種將
2023-09-07 16:18:51 148
148 具有很多有用的性質,因此在信號處理、通信和控制等領域中得到了廣泛的應用。下面就來介紹傅里葉變換的十大公式和性質。 一、傅里葉正變換 一般形式: $F(\omega) = \int_{-\infty}^{\infty}f(t)e^{-j\omega t}dt$ 其中,$f(t)$為時域信號,$F(\ome
2023-09-07 16:14:36 1210
1210 傅里葉變換的意義和理解 傅里葉變換是一種將一個信號在頻域中進行分解的數學工具,它將一個信號分解為不同頻率的正弦和余弦波的疊加。傅里葉變換的基本概念源于法國數學家約瑟夫·傅里葉,而其在現代通信、圖像
2023-09-07 16:08:42 3549
3549 由信號的分解可知,周期信號f(t)在區間(t0,t0+T)可以展開成在完備正交信號空間的無窮級數。如果完備的正交函數集是三角函數集或指數函數集,那么,周期信號所展開的無窮級數就分別稱為"三角型傅里葉級數"或"指數型傅里葉級數",統稱傅里葉級數。
2023-08-23 15:21:22 195
195 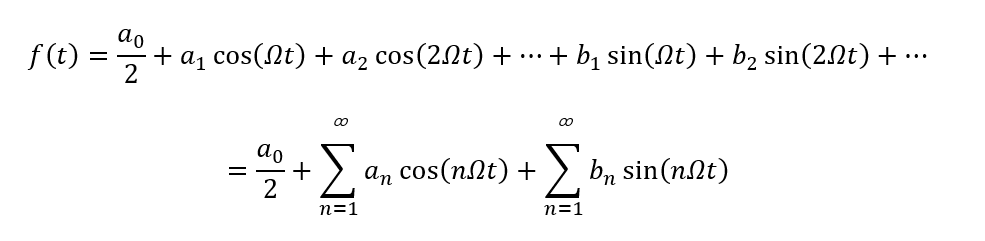
傅里葉級數——采用三角函數系(互為正交函數)進行正交展開
2023-08-09 15:00:31 304
304 
談到傅里葉級數,我們先要談傅里葉變換。籠統來說,傅里葉變換的目的將一個信號從時域變換到頻域進行分析,原因是很多在時域內看不見的特性在頻域內能很清楚地得到。
2023-08-09 11:51:02 610
610 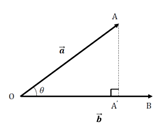
但傅里葉級數在數論、組合數學、信號處理、概率論、統計學、密碼學、聲學、光學等領域都有著廣泛的應用,這不由得讓人肅然起敬。一打開《信號與系統》、《鎖相環原理》等書籍,動不動就跳出一個“傅里葉級數”或“傅里葉變換”,弄一長串公式,讓人云山霧罩。
2023-07-17 10:18:49 199
199 
根據時域信號的表現的不同特點(連續或離散,周期或非周期),傅里葉分析有不同的類型,不同的叫法以示區別,如圖1所示。
2023-06-11 16:22:54 470
470 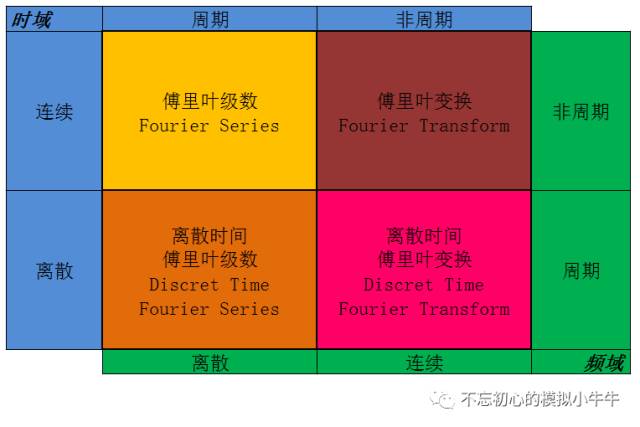
傅里葉級數真的優雅,一般書本上的習題也都是三角波、矩形波,積分起來相對容易。
2023-05-25 11:19:52 762
762 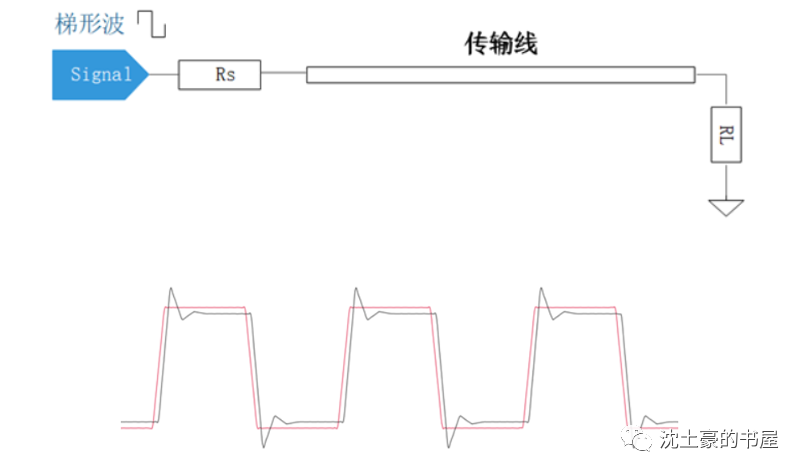
拉普拉斯變換與傅里葉變換的關系.ppt拉普拉斯變換與傅里葉變換的關系拉氏變換的引出,是針對 &
2009-09-16 08:42:31
了解傅里葉級數在電路分析和傅里葉級數方程中的重要性,同時深入了解該分析工具的工作原理。 這 傅里葉級數 是一個強大的工具,可以表達 非正弦周期波形 作為 正弦波形。在本文中,我們將首先通過介紹傅里葉
2023-01-27 14:11:00 587
587 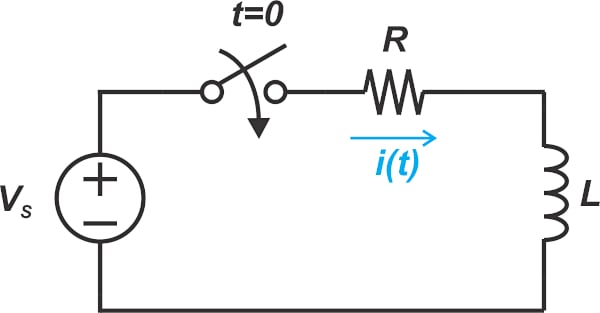
傅里葉級數在數論、組合數學、信號處理、概率論、統計學、密碼學、聲學、光學等領域都有著廣泛的應用,這不由得讓人肅然起敬。
2023-01-12 11:17:15 1876
1876 傅里葉變化只能對能量有限的信號進行變換(也就是可以收斂的信號),無法對能量無限的信號進行變換(無法收斂),因此,拉普拉斯應運而生,在原先的傅里葉變換公式中乘以一個衰減因子,使得無限能量的信號也能進行時頻變換。
2022-11-28 11:00:23 1013
1013 文章從實際出發,講述了什么是傅里葉變換,它的理論基礎以及Numpy和OpenCV實現傅里葉和逆傅里葉變換,并最終用高通濾波和低通濾波的示例。
2022-07-05 16:04:20 1025
1025 傅里葉逆變換就是傅里葉變換的逆過程,在F(ω)和求內積的時候,F(ω)只有t時刻的分量內積才會有結果,其余時間分量內積結果為0,同樣積分值是頻率從負無窮到正無窮的積分,就是把信號在每個頻率在t時刻上的分量疊加起來,疊加的結果就是f(t)在t時刻的值,這就回到了我們觀察信號最初的時域。
2022-03-14 10:14:19 3669
3669 FTIR傅里葉紅外光譜儀產品說明(英文版)
2021-11-05 17:24:04 1
1 從傅里葉級數、傅里葉變換推出拉普拉斯變換。
2021-06-23 16:25:27 5437
5437 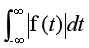
原信號的不同類型,傅里葉變換可以分為四種類別: (1)非周期性連續信號傅里葉變換 (2)周期性連續信號傅里葉級數 (3)非周期性離散信號離散時域傅里葉變換 (4)周期性離散信號離散傅里葉變換 快速傅里葉變換(FFT),是利用計算機計算離散傅里葉
2020-11-09 16:52:40 12009
12009 
的相關運算已經非常成熟,有現成函數可以調用。對于絕大部分只需用好傅里葉變換的同學,重要的不是去記那些枯燥的公式,而是解傅里葉變換的含義及意義。 本文試圖不用一個數學公式,采用較為通俗的語言深入淺出的闡述傅里葉變
2020-10-10 18:03:17 21666
21666 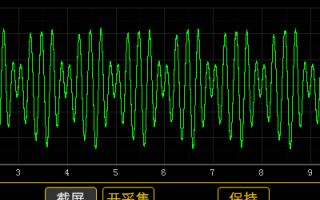
“傅里葉”這個名字,我相信對很多人來說并不陌生。尤其是理工科的童鞋,對這三個字應該是如雷貫耳。
2020-09-16 11:06:48 4144
4144 
了解周期序列的傅里葉級數及性質,掌握周期卷積過程
理解離散傅里葉變換及性質,掌握圓周移位、共軛對稱性,掌握圓周卷積、線性卷積及兩者之間的關系件
2020-04-13 08:00:00 1
1 法國數學家傅里葉發現,任何周期函數都可以用正弦函數和余弦函數構成的無窮級數來表示(選擇正弦函數與余弦函數作為基函數是因為它們是正交的)
2020-04-04 17:17:00 2514
2514 
傅里葉,Jean Baptiste Joseph Fourier(簡·巴普蒂斯·約瑟夫·傅里葉,1768/3/21-1830/5/16,法國男爵,數學家、物理學家,圖1-1),這位大魔王是很多理工科人的噩夢。
2019-12-06 15:36:00 77
77 本文檔的主要內容詳細介紹的是數字信號處理教程之DFT和FFT處理的學習課件免費下載包括了:1.離散傅里葉變換,2.與傅里葉變換的關系,3.與傅里葉級數的關系,4.DFT 窗效應,6.快速傅里葉變換。
2019-11-13 17:08:16 12
12 但傅里葉級數在數論、組合數學、信號處理、概率論、統計學、密碼學、聲學、光學等領域都有著廣泛的應用,這不由得讓人肅然起敬。一打開《信號與系統》、《鎖相環原理》等書籍,動不動就跳出一個“傅里葉級數”或“傅里葉變換”,弄一長串公式,讓人云山霧罩。
2019-06-29 09:34:34 118041
118041 
最近在看《信號與系統》,連續傅里葉級數和離散傅里葉級數中,離散傅里葉級數的諧波信號種類是有限的,而連續時間信號的傅里葉級數的諧波信號就有無數個,這個讓我很不解。
2019-06-01 09:28:49 1703
1703 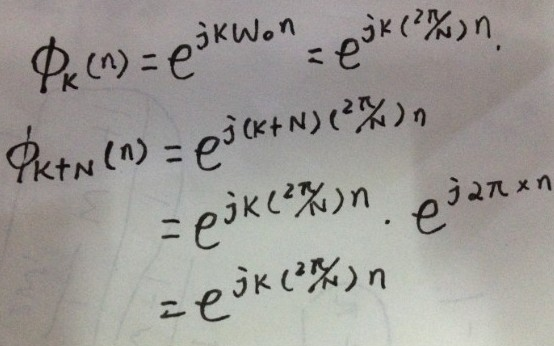
傅里葉變換是數字信號處理領城種很重要的算法。傅里葉表明:任何連續測量的時序或信號,都可以表示為不同頻率的正弦波信號的無限疊加。而根據該原理的傅里葉變換算法利用直接測量到的原始信號,以累加方式來計算該
2019-04-30 08:00:00 2
2 連續時間信號的頻域分析,是本課程最為重要的內容之一,也是考試的重點。包括三方面內容:周期信號的傅里葉級數、非周期信號的傅里葉變換、時域抽樣。本文對前兩個內容進行較為詳細的總結。
2018-05-19 09:15:28 50134
50134 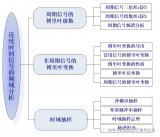
主要內容:
1.三角函數形式的傅氏級數
2.指數函數形式的傅氏級數
3.兩種傅氏級數的關系
4.頻譜圖
5.函數的對稱性與傅里葉級數的關系
6.周期信號的功率
7.傅里葉有限級數與最小方均誤差
2018-03-05 11:31:50 3
3 本文研究的目的是檢測不同光照下紡織工業中織布的瑕疵,不同光照下的織布圖像清晰度不同,但卻都非常有周期性,有方向性。所以本文提出了一種基于傅里葉極坐標變換的方法:該方法將圖像在頻域內的頻譜能量轉化到
2017-12-12 18:35:17 1
1 周期信號的頻譜分析——傅里葉級數
2017-12-06 14:27:04 2
2 典型周期信號的傅里葉級數
2017-12-06 14:25:17 1
1 一種積分變換,它來源于函數的傅里葉積分表示。積分稱為? 的傅里葉積分。拉普拉斯變換是工程數學中常用的一種積分變換,又名拉氏變換。拉氏變換是一個線性變換,可將一個有參數實數t(t≥ 0)的函數轉換為一個參數為復數s的函數。
2017-12-05 19:10:02 83345
83345 
小波與傅里葉分析基礎
有需要的朋友下來看看
2015-12-30 15:33:42 1
1 傅里葉分析不僅僅是一個數學工具,更是一種可以徹底顛覆一個人以前世界觀的思維模式。但不幸的是,傅里葉分析的公式看起來太復雜了,我保證這篇文章和你以前看過的所有文章都不同,讓大家了解傅里葉變換。
2014-05-29 09:33:36 49120
49120 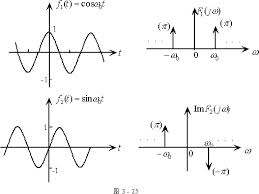
傅里葉分析不僅僅是一個數學工具,更是一種可以徹底顛覆一個人以前世界觀的思維模式。但不幸的是,傅里葉分析的公式看起來太復雜了,我保證這篇文章和你以前看過的所有文章都不同,讓大家了解傅里葉變換。
2014-05-27 09:11:32 250363
250363 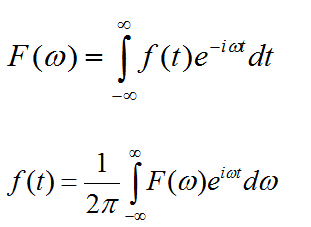
電子發燒友網站提供《小波與傅里葉分析基礎_中文版_.txt》資料免費下載
2012-07-07 13:32:19 16
16 向讀者展示傅里葉分析和小波的許多基礎知識以及在信號分析方面的應用。全書分為8章和3個附錄,第0章是學習第1章至第7章的準備知識,即內積空間;第1章講解傅里葉級數的基礎知識
2011-07-14 11:25:20 195
195 摘要用球面波照明物體的自由空間菲涅耳衍射3實現分數(p1)級傅里葉逆變換,提供了分數傅里葉 逆變換無透鏡光學實現的模式及其參量選擇的法則,對光學信息處理具有實用價值.計算機模擬實驗證明了結論的可靠與可行. 關鍵詞:分數級,傅里葉,逆變換
2011-02-23 09:35:17 29
29 連續信號的傅里葉分析:信號分析就是要研究信號如何表示為各分量的疊加,并從信號分量的組成情況去考察信號的特性。由上一章的討論可知,連續時間信號可以表示為基本信號
2009-10-04 09:21:54 35
35 序列的傅里葉變換(DTFT) :DTFT:Discrete-time Fourier transform為研究離散時間系統的頻率響應作準備,從抽樣信號的傅里葉變換引出:二.傅氏變換、拉氏變換、z變換的關系1. 三
2009-09-30 19:38:25 36
36 非周期信號的傅里葉變換
前面已討論了周期非正弦信號的傅里葉級數展開,下面來分析非周期信號的傅里葉變換。當周期
2009-07-27 10:23:30 7992
7992 非正弦周期信號的傅里葉級數分解
前面章節中已對直流電路與正弦交流電路的分析計算方法作了詳細介紹,當電路的激勵
2009-07-27 10:20:16 21863
21863 快速付里葉變換:一、快速付里葉變換FFT有 限 長 序 列 通 過 離 散 傅 里 葉 變 換 (D F T) 將 其 頻 域 離 散 化 成 有 限 長 序 列 . 但 其 計算 量 太 大, 很 難 實 時 地 處
2009-07-25 11:43:24 76
76 1)付里葉變換的四種形式(2)離散付里葉級數(3)離散付里葉變換(4)離散付里葉變換的有關性質(5)頻率抽樣理論(6)離散付里葉變換的應用(7)DFT逼近連
2009-07-25 11:42:30 14
14 Z變換與拉氏變換、傅氏變換的關系:一.Z變換與拉氏變換的關系1.理想抽樣信號的拉氏變換設為連續信號, 為其理想抽樣信號,則
2.Z變換與拉氏變換的關系( S、Z平面映
2009-07-25 10:32:44 40
40 離散傅里葉變換及其快速算法離散傅里葉變換 (Discrete Fourier Transform,DFT)是時間函數是離散的,而且頻譜函數也是離散的變換。3. 1 討論周期序列的 傅里葉級數及其性質。
2008-10-30 12:54:54 33
33 三角函數形式的傅氏級數 指數函數形式的傅氏級數兩種傅氏級數的關系 頻譜圖函數的對稱性與傅里葉級數的關系周期信號的功率傅里葉
2008-08-05 12:22:02 38
38 從本章開始由時域轉入變換域分析,首先討論傅里葉變換。傅里葉變換是在傅里葉級數正交函數展開的基礎上發展而產生的,這方面的問題也稱為傅里葉分析(頻域分析)。將信號
2008-08-05 11:49:37 50
50
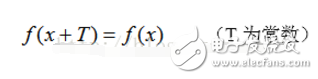

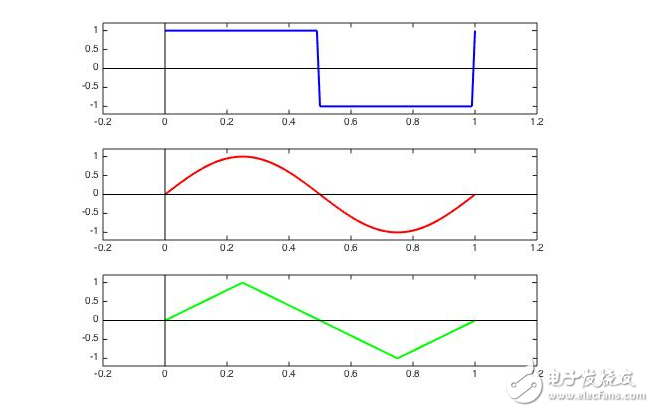
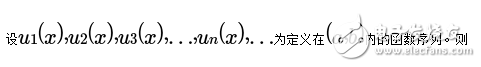
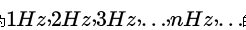
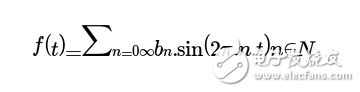

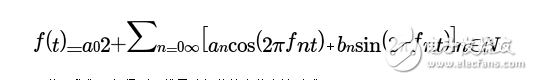


![]() 趨于零。也就是說,一個非周期函數會通過傅里葉變換被描述成連續的正弦函數的組合,即在頻域上連續。基于這個思想,傅里葉級數即將演化成傅里葉變換。
趨于零。也就是說,一個非周期函數會通過傅里葉變換被描述成連續的正弦函數的組合,即在頻域上連續。基于這個思想,傅里葉級數即將演化成傅里葉變換。
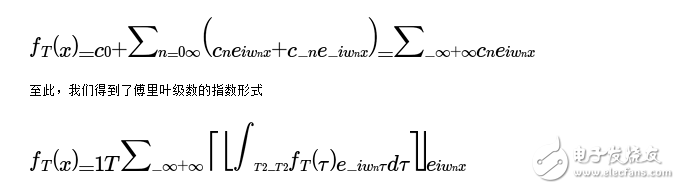




 電子發燒友App
電子發燒友App










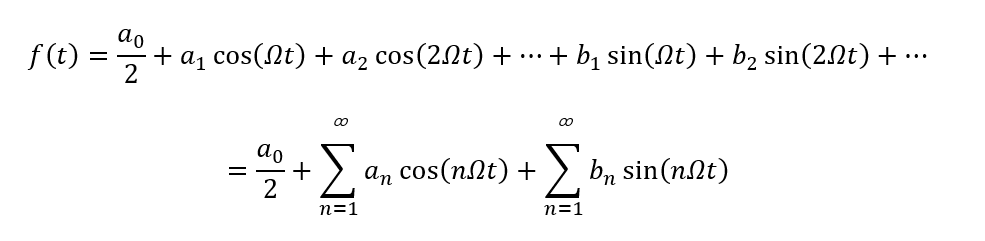














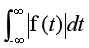


















評論