這一期接著聊連續(xù)時間的傅里葉分析，主要內(nèi)容如下。

1、大牛傅里葉的簡介；

2、傅里葉級數(shù)到傅里葉變換的轉(zhuǎn)換過程；

3、周期信號的傅里葉變換表示；

4、卷積和乘法在時域及頻域的對偶關(guān)系。

上一期，我們講到了連續(xù)時間周期信號的傅里葉級數(shù)展開。傅里葉的名字可謂聲名遠播，是個不得不聊的人物。

約瑟夫·傅里葉(1768-1830)，法國數(shù)學(xué)家，物理學(xué)家。一生富有傳奇色彩。兒時淪為孤兒，長大后，扛過槍，當過地方行政長官，出將入相。又那么熱愛學(xué)習(xí)。在研究熱傳導(dǎo)問題時，于1811年，通過論文《熱的傳播》提出了任一函數(shù)可以展開成三角函數(shù)的無窮級數(shù)，也就是上一期中關(guān)于傅里葉級數(shù)的內(nèi)容，積分變換基礎(chǔ)。

1822年，出版專著《熱的解析理論》將三角函數(shù)級數(shù)的理論一般化。將周期信號推廣到更一般的信號，更系統(tǒng)地總結(jié)歸納為傅里葉分析。

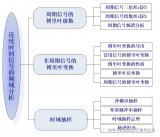
根據(jù)時域信號的表現(xiàn)的不同特點（連續(xù)或離 散 ，周期或 非周期 ），傅里葉分析有不同的類型，不同的叫法以示區(qū)別，如圖1所示。這里也看到了時域和頻率的對偶性（Duality）。這期還是先討論連續(xù)時間類型，對于離散情況，后續(xù)會專門總結(jié)。

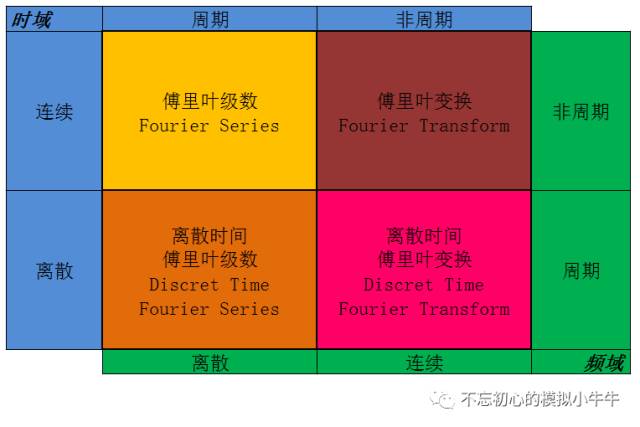
圖1

傅里葉變換可以認為是對傅里葉級數(shù)結(jié)論的一般化推廣過程，這里先給出兩個動圖說明這個趨近過程。其中圖2是上一篇(積分變換基礎(chǔ)中講到的定義在區(qū)間[-1,1]的三角波，周期T=2。隨著周期T增加，并趨近于+∞，信號就等效為單周期的三角波（其他定義域的值都為零）。

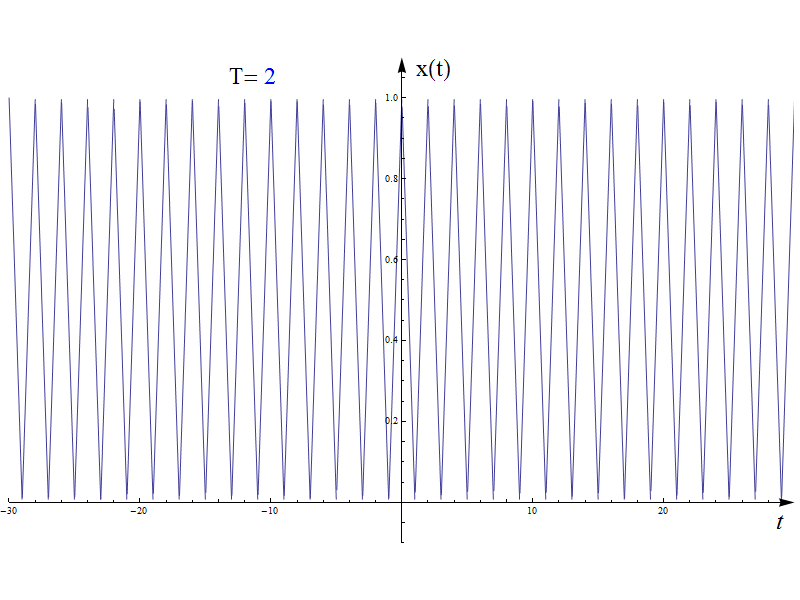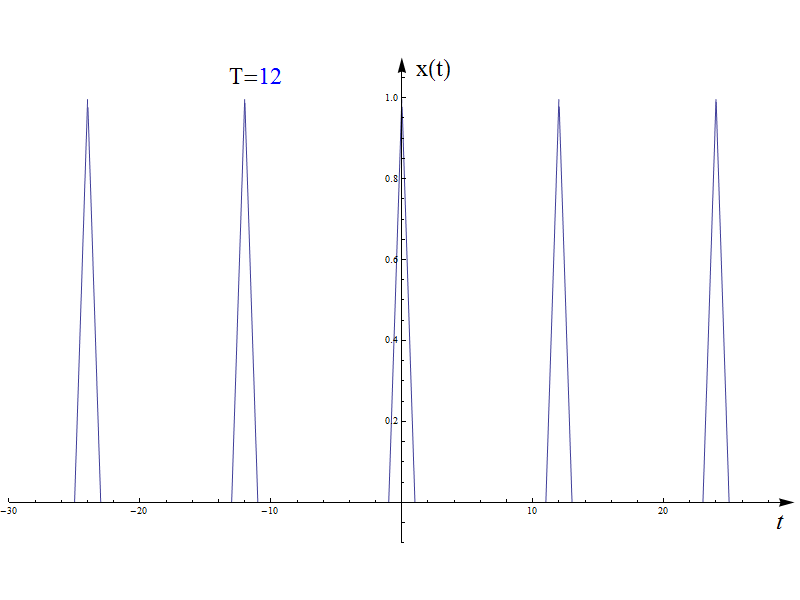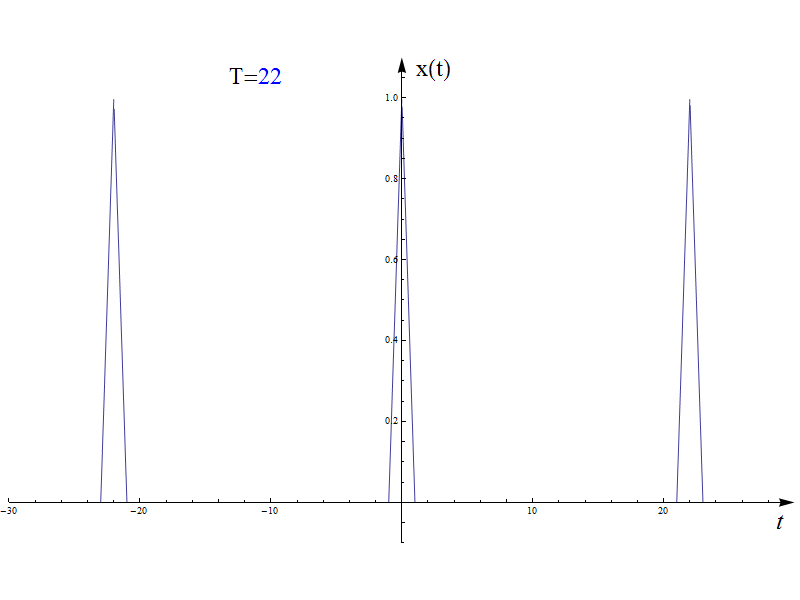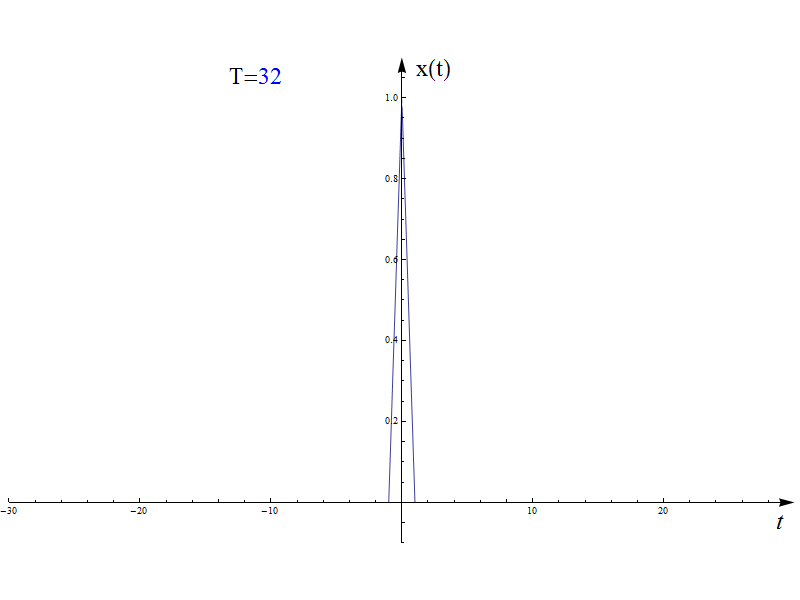
圖2

當周期T增加時，其傅里葉級數(shù)ak和周期T乘積的變化過程如圖3中藍色的離散幅值，紅色為akT的包絡(luò)線。至于為什么是akT的乘積，我們先留個疑問。

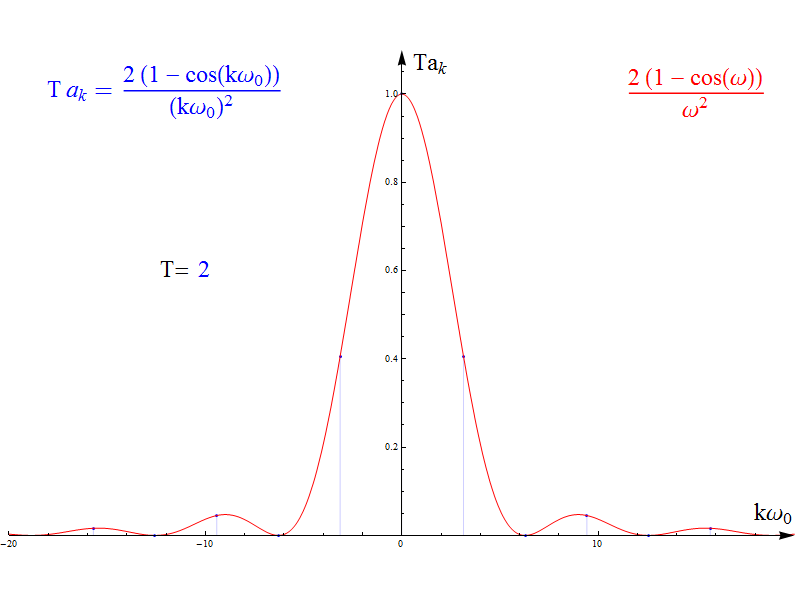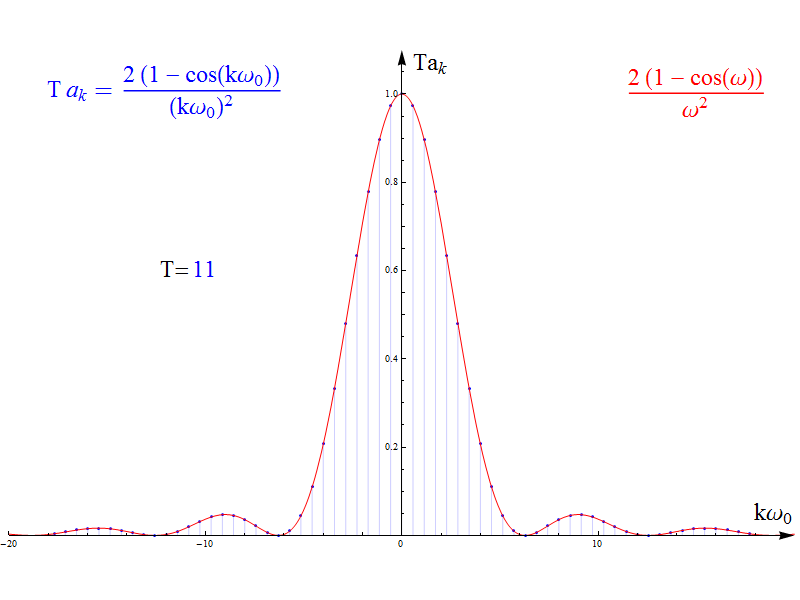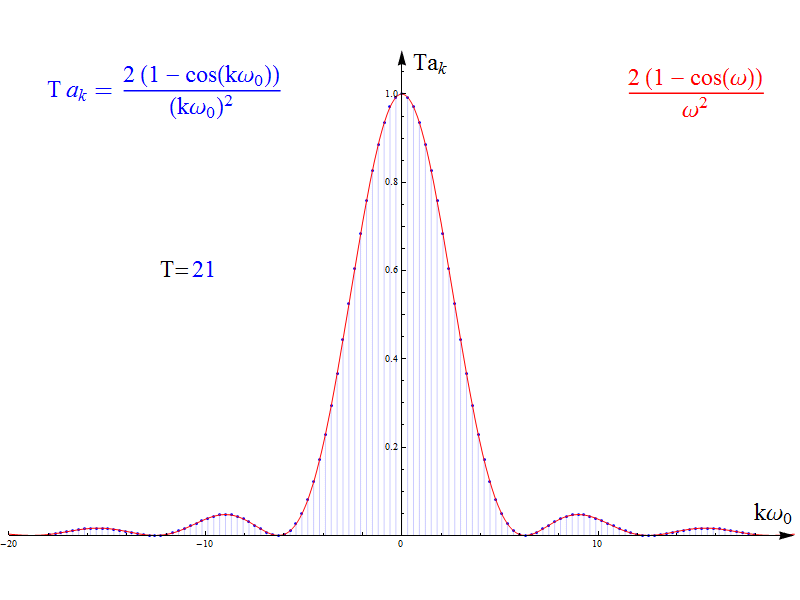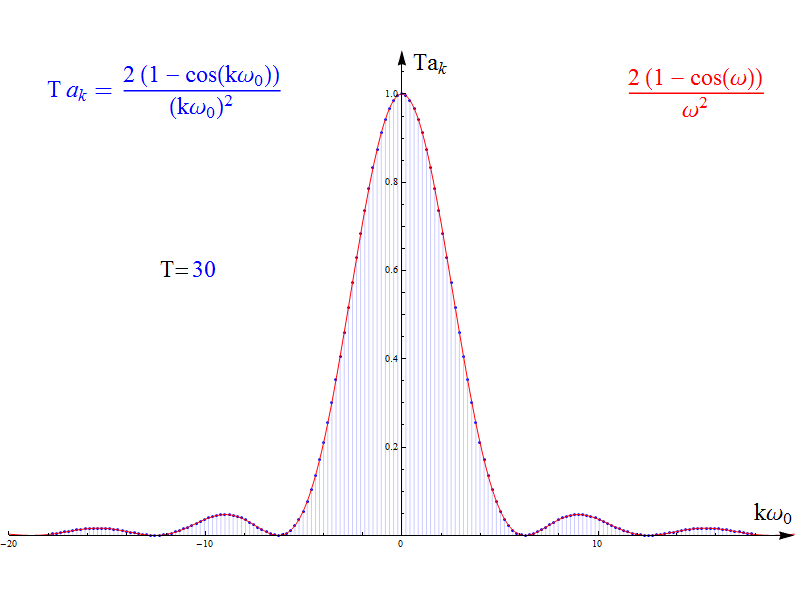
圖3

圖2和3可以看到，當周期T增加時，時域信號越來越稀疏，而其傅里葉級數(shù)的頻譜卻越來越密集。直覺相信，在極限情況下，其終極形態(tài)就是 紅色的包絡(luò)線函數(shù) 。

下邊試著從極限的角度，理清如何將周期信號傅里葉級數(shù)轉(zhuǎn)化為非周期信號的 傅里葉變換 。

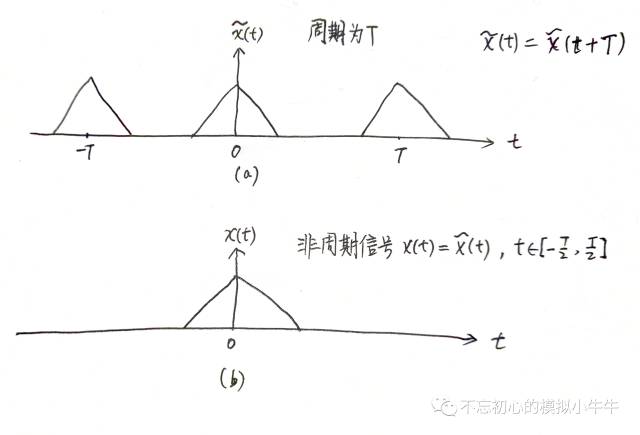
圖4

圖4重新給出了周期為T的周期信號圖4(a)和其極限情況，僅定義在-T/2和T/2區(qū)間的非周期信號圖4(b)。

圖4(a)周期信號的傅里葉級數(shù)系數(shù)如圖5。通過變形，注意和定義函數(shù) X(jω) 的關(guān)系。 X(jω) 就是akT的包絡(luò)線函數(shù)。

圖5

我們再看看圖4(a)周期信號的傅里葉級數(shù)表示。利用圖5的包絡(luò)線函數(shù) X(jω) 定義，可以看到圖6中的階梯型面積之和。極限情況下，等于被積函數(shù) X(jω)e^(j ωt ) 和ω軸形成面積。

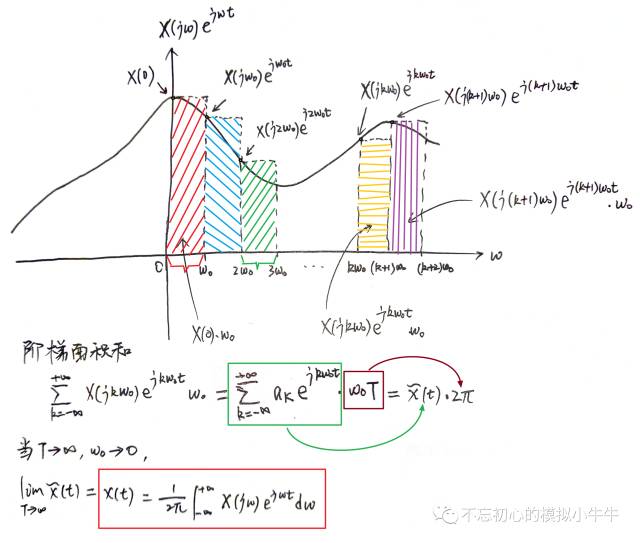
圖6

把傅里葉變換對重寫如圖7所示。時域信號x(t)的表示從周期信號的 線性累加 ，變成非周期信號的積分表示形式。注意其傅里葉變換實際上是 復(fù)變函數(shù) ，自變量為jω，僅僅位于復(fù)平面的虛軸上。函數(shù)值也為復(fù)數(shù)形式，同時包含了幅度和相位的信息復(fù)合形式。

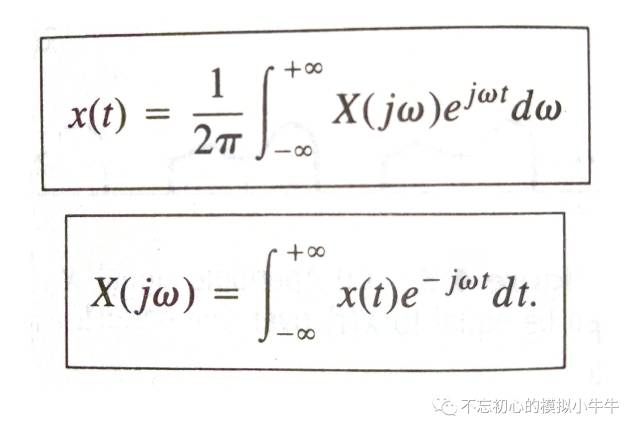
圖7

注意傅里葉變換 X(jω) 的積分結(jié)果收斂存在，同樣需要滿足狄利克雷條件。

針對時域一般信號，通過傅里葉變換對，將信號從時域和頻域緊密的聯(lián)系在一起，建立了人們認識問題的新角度。從頻域分析去解釋問題也能夠很好的符合人們實驗觀測的結(jié)果。使傅里葉變換在現(xiàn)代眾多技術(shù)領(lǐng)域中得到廣泛應(yīng)用。

我們希望能夠?qū)⒏道锶~變換推廣到更寬的適用范圍。就必須解釋和回答第三個問題，周期信號如何用傅里葉變換來表示？

如圖8所示，首先考慮頻域中位于頻率點（ kω0 ）處的單位沖激函數(shù)。單位沖激函數(shù)（出于傅里葉級數(shù)的頻譜是離散頻率點的若干值，所以考慮頻域的單位沖激函數(shù)）的傅里葉反變換對應(yīng)的時域信號應(yīng)該是什么樣的。

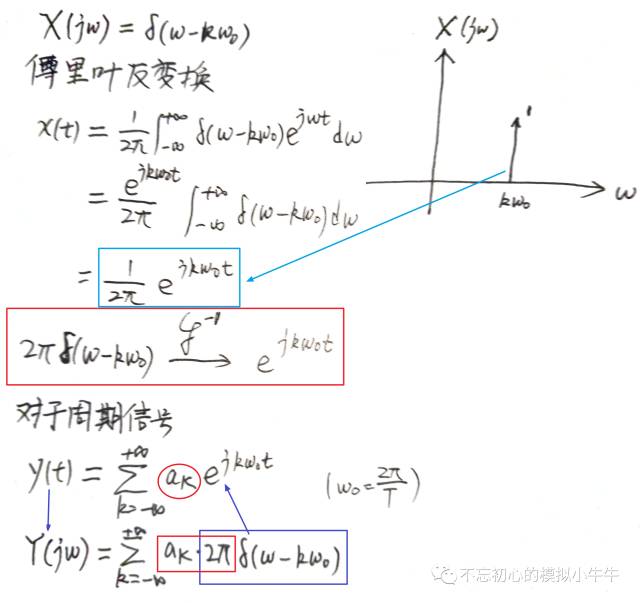
圖8

圖8中可給出了周期信號的傅里葉變化表示，是在k次諧波位置，為ak乘2π的離散頻譜形式。(注意2πak****也是包含了幅度和相位的符合信息，也就是說是復(fù)數(shù)形式)

從時域和頻域不同角度分析，就像觀察硬幣的正反面。雖然觀測角度不同，事物本質(zhì)上是一致的。就像歷史上人們對電磁波的認識過程，到底是“波”還是“粒子”，是人們對電磁波“波粒二象性”不同角度的觀測結(jié)果。

圖9

就像我們對聲音的理解一樣，物體的振動產(chǎn)生聲音。不同的樂器，根據(jù)同樣的樂譜，都能演奏出近乎一樣的樂曲（音色有各自的特色）。實際感受到的是悅耳動聽的音樂（時域）。樂譜就算是從頻域記錄音樂的方式。

傅里葉變換中兩個重要到不能再重要的關(guān)系，值得我們重點回顧一下，卷積和 乘法 。兩者之間的相互轉(zhuǎn)換的近似性關(guān)系稱之為 對偶性（Duality） 。

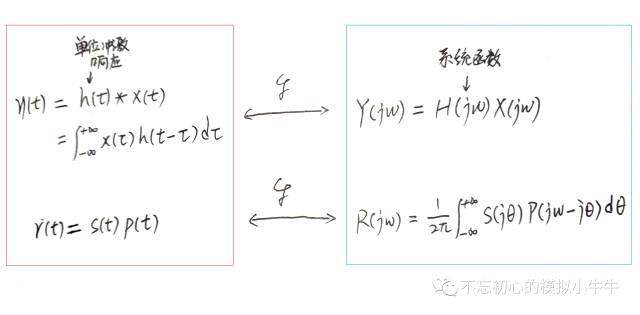
圖10

我們知道，時域卷積是信號與系統(tǒng)的基礎(chǔ)概念，時域中，需要通過卷積運算計算系統(tǒng)響應(yīng)。相信很多人，都知道卷積這概念，要真是讓大家通過卷積來推導(dǎo)一下時域中系統(tǒng)響應(yīng)。估計還是要撓撓頭皮的。相反，時域的卷積運算映射到頻域，仿佛一下子就降級到了只需要小學(xué)生的運算能力了，即乘法。從而大幅度降低運算復(fù)雜性，也符合我們一貫懶惰的本性。

轉(zhuǎn)換為頻域乘法，一個簡單概念為濾波器。從頻域角度描，對不同頻率分量的幅度和相位進行需要的衰減和增強等操作。

另一個就是時域的乘法，映射到頻域為卷積運算，貌似變復(fù)雜了。

其實在通信領(lǐng)域，時域乘法具有重要的意義。為了提高通信過程中傳遞信息的效率和距離。通常會將有用信息調(diào)制（Mixer乘法器）到高頻率的載波上，便于信息的傳遞。接收端接收后，又需要把有用信息摘出。（原諒我這非專業(yè)人士的蹩腳描述）。其頻域解釋就是頻譜搬移，將有用信號從低頻搬移到高頻載波上。

如圖11，在高中的三角函數(shù)的學(xué)習(xí)過程中。比如說“積化和差”，如果把角度換做角頻率。我們仔細再思考一下，肯定會會心一笑。這就是最基礎(chǔ)的模擬調(diào)制方式，調(diào)幅（amplitude modulation）。

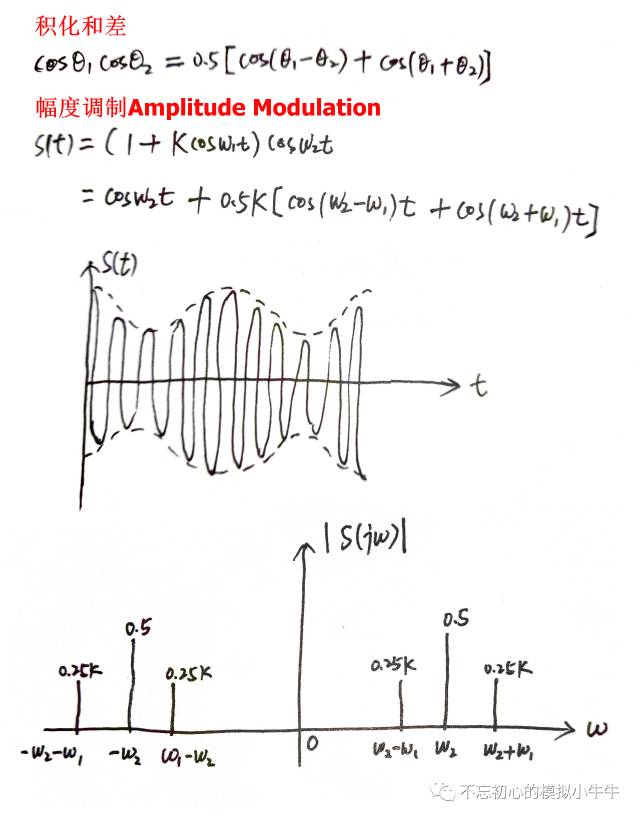
圖11

再舉一個例子，在后續(xù)回顧離散傅里葉變換（DTFT）時，也會看到為避免時域信號周期延拓后出現(xiàn)頻譜泄露，需要對時域采樣加 "窗函數(shù)" 。這也是一個在時域做乘積的例子，到時候，我們再仔細思考。

關(guān)于傅里葉變換的各種性質(zhì)這里就不詳細介紹了，大家還是翻翻書，多記多用才行。