貝葉斯濾波和卡爾曼濾波是兩種常用的濾波方法,它們在信號處理、導航、機器人定位等領域有著廣泛的應用。
- 貝葉斯濾波
1.1 貝葉斯濾波的基本原理
貝葉斯濾波是一種基于貝葉斯理論的濾波方法。它通過將先驗概率和觀測數據相結合,來估計系統的狀態。貝葉斯濾波的核心思想是:在給定觀測數據的情況下,系統狀態的后驗概率可以通過貝葉斯公式進行計算。
貝葉斯公式如下:
P(A|B) = P(B|A) * P(A) / P(B)
其中,P(A|B)表示在觀測到B的情況下,事件A發生的概率;P(B|A)表示在事件A發生的情況下,觀測到B的概率;P(A)和P(B)分別表示事件A和B的先驗概率。
在貝葉斯濾波中,我們通常將系統狀態表示為隨機變量X,觀測數據表示為隨機變量Z。貝葉斯濾波的目標是計算在給定觀測數據Z的情況下,系統狀態X的后驗概率P(X|Z)。
1.2 貝葉斯濾波的步驟
貝葉斯濾波主要包括以下幾個步驟:
- 初始化:根據先驗知識,設定系統狀態的初始概率分布P(X0)。
- 預測:根據系統模型,計算下一時刻系統狀態的先驗概率分布P(Xt|Zt-1)。這一步通常需要考慮系統的狀態轉移概率。
- 更新:根據觀測數據,使用貝葉斯公式更新系統狀態的后驗概率分布P(Xt|Zt)。
- 重復步驟2和3,直到完成所有觀測數據的處理。
1.3 貝葉斯濾波的優點
- 靈活性:貝葉斯濾波可以處理各種類型的先驗概率分布和觀測模型,具有很強的適應性。
- 魯棒性:貝葉斯濾波在處理噪聲和異常值方面具有較好的魯棒性。
- 可解釋性:貝葉斯濾波的結果具有很好的可解釋性,可以直觀地反映系統狀態的不確定性。
1.4 貝葉斯濾波的缺點
- 計算復雜性:貝葉斯濾波需要計算和更新概率分布,計算量較大,尤其是在高維空間中。
- 先驗知識依賴性:貝葉斯濾波的性能很大程度上依賴于先驗知識的準確性。
- 卡爾曼濾波
2.1 卡爾曼濾波的基本原理
卡爾曼濾波是一種線性最優濾波方法,它基于線性系統和高斯噪聲的假設。卡爾曼濾波的核心思想是通過最小化預測誤差的方差,來估計系統的狀態。
在卡爾曼濾波中,系統的狀態和觀測數據通常表示為向量形式。系統的狀態轉移和觀測模型都是線性的,且噪聲是高斯分布的。卡爾曼濾波的目標是計算在給定觀測數據的情況下,系統狀態的最優估計。
2.2 卡爾曼濾波的步驟
卡爾曼濾波主要包括以下幾個步驟:
- 初始化:根據先驗知識,設定系統狀態的初始估計值和協方差矩陣。
- 預測:根據系統模型,計算下一時刻系統狀態的預測值和預測協方差矩陣。
- 更新:根據觀測數據,計算卡爾曼增益,然后更新系統狀態的估計值和協方差矩陣。
- 重復步驟2和3,直到完成所有觀測數據的處理。
2.3 卡爾曼濾波的優點
- 計算效率:卡爾曼濾波的計算量相對較小,尤其是在線性系統和高斯噪聲的假設下。
- 穩定性:卡爾曼濾波具有很好的穩定性,可以保證濾波結果的可靠性。
- 可擴展性:卡爾曼濾波可以很容易地擴展到多維系統和多傳感器融合的場景。
2.4 卡爾曼濾波的缺點
- 線性和高斯噪聲假設:卡爾曼濾波的性能很大程度上依賴于線性系統和高斯噪聲的假設,對于非線性或非高斯噪聲的系統,其性能可能會受到影響。
- 敏感性:卡爾曼濾波對初始估計值和協方差矩陣的敏感性較高,不準確的初始值可能導致濾波結果的偏差。
- 可解釋性:卡爾曼濾波的結果不如貝葉斯濾波直觀,可能需要額外的解釋和分析。
-
數據
+關注
關注
8文章
7242瀏覽量
91039 -
信號處理
+關注
關注
48文章
1055瀏覽量
103923 -
卡爾曼濾波
+關注
關注
3文章
166瀏覽量
24985
發布評論請先 登錄





 貝葉斯濾波和卡爾曼濾波的區別
貝葉斯濾波和卡爾曼濾波的區別
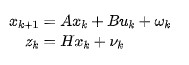
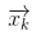
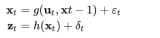










評論