1 前言
在很多實際工程問題當中,非線性系統占大多數,而卡爾曼提出來的卡爾曼濾波器是一種針對線性系統的估計算法[1]。 為了解決這一問題,Schmidt學者分析了卡爾曼濾波器中的系統模型部分,并提出將卡爾曼理論應用到非線性系統的擴展卡爾曼算法 Extended Kalman Filter(EKF)[2]。相比于線性卡爾曼濾波器,擴展卡爾曼濾波器有更廣的適用范圍[3, 4],更高的狀態估計精度,可以處理任意更新頻率的系統。 有了上文的基礎,這里,我們將通過一個二維小車的例子并來介紹擴展卡爾曼濾波的原理。
2 擴展卡爾曼濾波算法介紹
在介紹擴展卡爾曼濾波算法之前,我們先回憶一下之前介紹的卡爾曼濾波算法:
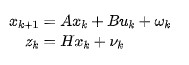
其中前兩個公式為系統狀態預測部分,后三個公式為系統的修正部分。其中整個系統最重要的是要通過公式將系統的模型和測量與狀態之間的關系表示出來:
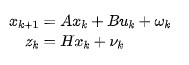
式中為系統矩陣,為控制矩陣,為觀測矩陣。為目標在時刻的狀態,為控制量,和分別為系統誤差和測量誤差。在線性卡爾曼濾波算法中,和是常值矩陣,其對應的系統就是線性系統。如果想將卡爾曼理論應用到非線性系統中,則需要對非線性系統進行線性化處理。
2.1 擴展卡爾曼濾波算法的不同
非線性系統方程及其觀測方程通常可以表示為:
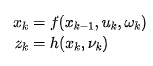
擴展卡爾曼濾波算法可以通過將非線性系統在其參考點處做泰勒級數展開,從而使非線性系統可以線性化。展開后,我們可以得到:
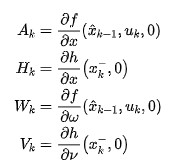
其中和是非線性系統函數在時刻求偏導數后的雅可比矩陣,和為非線性測量函數求偏導數后的雅克比矩陣。那么,擴展卡爾曼濾波算法可以寫成:
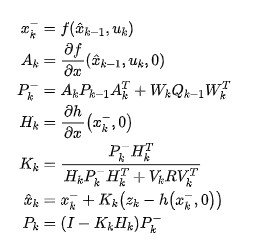
介紹完公式,接下來我們將通過2維平面內的小車來對擴展卡爾曼濾波算法進行講解。
3 二維小車實例
如果要估計一個在二維平面內運動的小車,首先要根據要求選擇一個較為合適的系統模型。在二維平面內,小車的運動可能是直線也可能是曲線,那么在一維平面用的線性勻速模型constant velocity model(CV) 將不適用。這里將采用一個簡單的非線性模型勻轉速、速度模型 constant turning rate and velocity magnitude model(CTRV)。
3.1 非線性模型CTRV
ctrv模型是cv模型的一般形式。這里我們假設觀測到的狀態變量為:
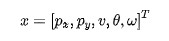
分別對應目標在,方向上的位置,速度,角度和角速度,變量之間的關系如圖1所示。
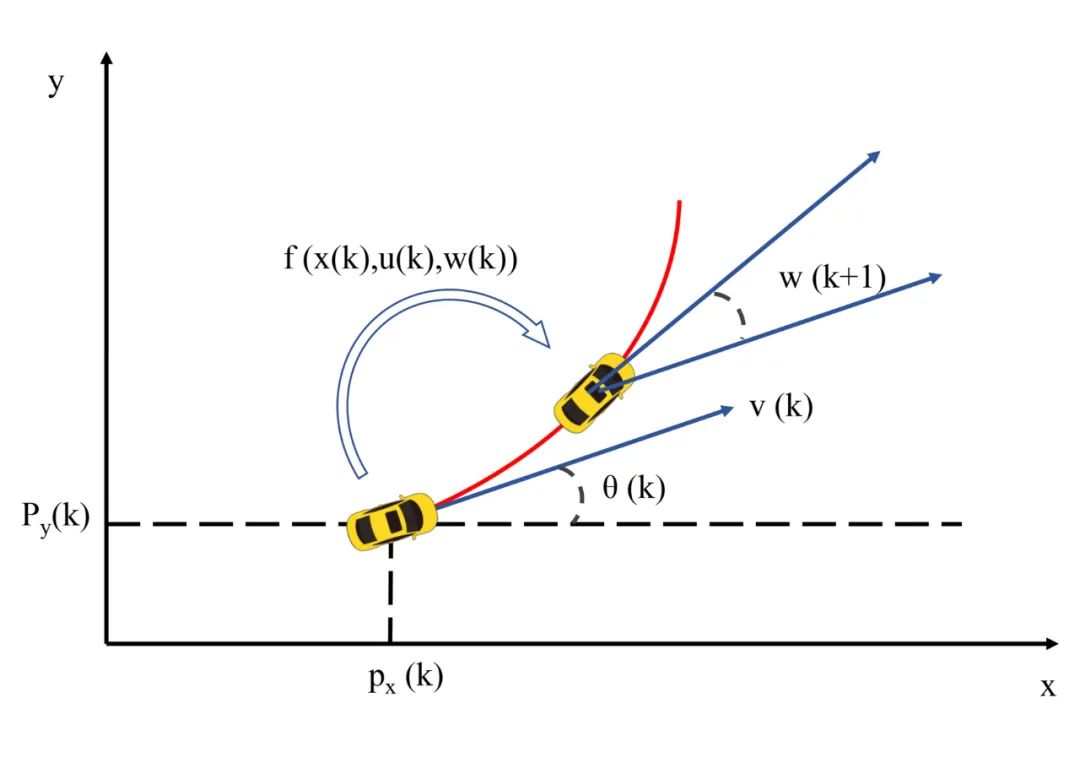
圖 1: 二維平面ctrv模型
狀態量關系從圖中可以看出,各變量之間的相互關系。那么,從時刻到時刻,狀態的變化應該是:
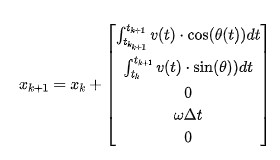
根據積分,我們可以得到下式:
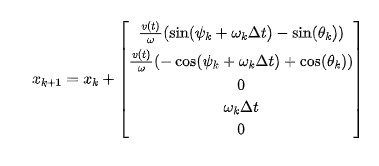
這里,我們對系統函數求偏導得到其雅克比矩陣為
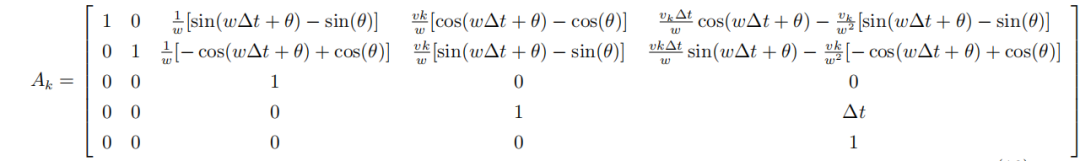
這里為了將系統誤差為:
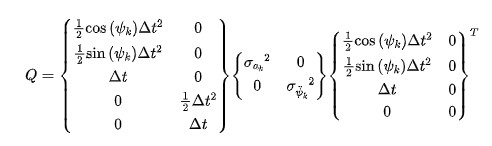
后續再套入到卡爾曼濾波器中,我們就可以得到一個CTRV的跟蹤模型:
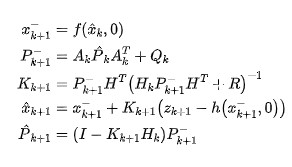
3.2 仿真
這里我們假設二維小車系統可以觀測到目標的位置:
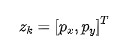
那么觀測方程為:
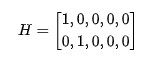
仿真總時間10s,時間間隔,目標小車繞原點,半徑以速度做勻速圓周運動。觀測信息為目標的位置,測量誤差。
從視頻中我們可以看到,不同的模型即使在當前估計狀態相差不大的情況下,其估計目標未來的狀態也是有很大差別的。在這個例子中,目標做的是勻速繞圈運動,CTRV模型更能描述系統的運動狀態,但該模型是非線性系統。因此,需要結合EKF,來實現對非線性系統的狀態跟蹤和預測。
仿真結果如圖2所示,紅色軌跡為小車真實軌跡,紅點為測量小車位置,藍色圓圈為CV模型估計的小車當前位置,綠色圓圈為CTRV模型估計的小車當前位置,藍色實線為CTRV模型估計小車軌跡,藍色虛線為CTRV模型預測未來一段時間內的小車軌跡,綠色實線為CV模型估計小車軌跡,綠色虛線為CV模型預測未來一段時間內的小車軌跡。可以看出CTRV模型的預測比CV模型的預測在繞圈運動中更為準確。
4 總結
在很多實際工程問題中,系統的描述總存在不同程度的非線性,如平方、三角函數等。針對這一問題,EKF的思路是將非線性系統線性化轉換為近似的線性系統,然后應用卡爾曼濾波算法完成狀態估計。
審核編輯:湯梓紅
-
濾波器
+關注
關注
162文章
8068瀏覽量
181012 -
濾波算法
+關注
關注
2文章
89瀏覽量
13902 -
卡爾曼濾波器
+關注
關注
0文章
54瀏覽量
12337
原文標題:擴展卡爾曼濾波器介紹
文章出處:【微信號:雨飛工作室,微信公眾號:雨飛工作室】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄

基于DSP的擴展卡爾曼濾波直流無刷電機控制
自由轉子陀螺的漂移誤差模型識別系統
擴展卡爾曼濾波在永磁同步電機無位置傳感器控制中的應用詳細概述
基于擴展卡爾曼濾波等的齒輪嚙合剛度辨識算法
基于擴展卡爾曼濾波的機動目標航跡跟蹤
基于擴展卡爾曼濾波EKF的無感控制+Matlab/Simulink仿真案例





 擴展卡爾曼濾波的原理
擴展卡爾曼濾波的原理

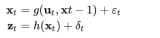










評論