使用C++構(gòu)建一個(gè)二叉樹(shù)并輸出。
輸入
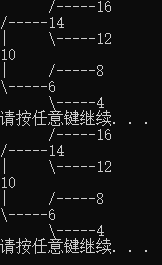
輸入根節(jié)點(diǎn)為10,依次輸入6、4、8、14、12、16
代碼如下:
#include 輸出
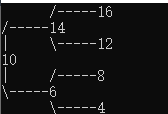
審核編輯:湯梓紅
聲明:本文內(nèi)容及配圖由入駐作者撰寫(xiě)或者入駐合作網(wǎng)站授權(quán)轉(zhuǎn)載。文章觀(guān)點(diǎn)僅代表作者本人,不代表電子發(fā)燒友網(wǎng)立場(chǎng)。文章及其配圖僅供工程師學(xué)習(xí)之用,如有內(nèi)容侵權(quán)或者其他違規(guī)問(wèn)題,請(qǐng)聯(lián)系本站處理。
舉報(bào)投訴
-
圖形
+關(guān)注
關(guān)注
0文章
71瀏覽量
19571 -
C++
+關(guān)注
關(guān)注
22文章
2117瀏覽量
74777 -
二叉樹(shù)
+關(guān)注
關(guān)注
0文章
74瀏覽量
12560
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
熱點(diǎn)推薦
計(jì)算機(jī)二級(jí)二叉樹(shù)的問(wèn)題
各位大神,本人馬上要考計(jì)算機(jī)二級(jí)了,那個(gè)二叉樹(shù)老是弄不明白,比如一個(gè)題目,一棵二叉樹(shù)共有25個(gè)節(jié)點(diǎn),其中五個(gè)葉子節(jié)點(diǎn),則度為1的節(jié)點(diǎn)數(shù)為?
發(fā)表于 09-04 09:45
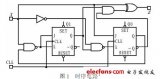
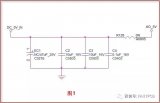
基于二叉樹(shù)的時(shí)序電路測(cè)試序列設(shè)計(jì)
為了實(shí)現(xiàn)時(shí)序電路狀態(tài)驗(yàn)證和故障檢測(cè),需要事先設(shè)計(jì)一個(gè)輸入測(cè)試序列。基于二叉樹(shù)節(jié)點(diǎn)和樹(shù)枝的特性,建立時(shí)序電路狀態(tài)二叉樹(shù),按照電路二叉樹(shù)節(jié)點(diǎn)(狀態(tài))與樹(shù)枝(輸入)的層次邏輯
發(fā)表于 07-12 13:57
?0次下載
二叉樹(shù)層次遍歷算法的驗(yàn)證
實(shí)現(xiàn)二叉樹(shù)的層次遍歷算法,并對(duì)用”A(B(D,E(H(J,K(L,M(,N))))),C(F,G(,I)))”創(chuàng)建的二叉樹(shù)進(jìn)行測(cè)試。
發(fā)表于 11-28 01:05
?2194次閱讀
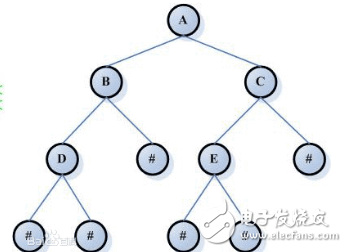
二叉樹(shù),一種基礎(chǔ)的數(shù)據(jù)結(jié)構(gòu)類(lèi)型
然后我們?cè)?b class='flag-5'>定義一棵深度也為 3 的二叉樹(shù),該二叉樹(shù)的 n 個(gè)結(jié)點(diǎn)(n≤7),當(dāng)從 1 到 n 的每個(gè)結(jié)點(diǎn)都與上圖中的編號(hào)結(jié)點(diǎn)一一對(duì)應(yīng)時(shí),這二叉樹(shù)就稱(chēng)為完全
詳解電源二叉樹(shù)到底是什么
作為數(shù)據(jù)結(jié)構(gòu)的基礎(chǔ),樹(shù)分很多種,像 AVL 樹(shù)、紅黑樹(shù)、二叉搜索樹(shù)....今天我想分享的是關(guān)于二叉樹(shù)
C語(yǔ)言二叉樹(shù)代碼免費(fèi)下載
本文檔的主要內(nèi)容詳細(xì)介紹的是C語(yǔ)言二叉樹(shù)代碼免費(fèi)下載。
發(fā)表于 08-27 08:00
?1次下載
紅黑樹(shù)(Red Black Tree)是一種自平衡的二叉搜索樹(shù)
平衡(Balance):就是當(dāng)結(jié)點(diǎn)數(shù)量固定時(shí),左右子樹(shù)的高度越接近,這棵二叉樹(shù)越平衡(高度越低)。而最理想的平衡就是完全二叉樹(shù)/滿(mǎn)二叉樹(shù),高度最小的二叉樹(shù)。
二叉樹(shù)操作的相關(guān)知識(shí)和代碼詳解
樹(shù)是數(shù)據(jù)結(jié)構(gòu)中的重中之重,尤其以各類(lèi)二叉樹(shù)為學(xué)習(xí)的難點(diǎn)。在面試環(huán)節(jié)中,二叉樹(shù)也是必考的模塊。本文主要講二叉樹(shù)操作的相關(guān)知識(shí),梳理面試常考的內(nèi)容。請(qǐng)大家跟隨小編一起來(lái)復(fù)習(xí)吧。 本篇針對(duì)面
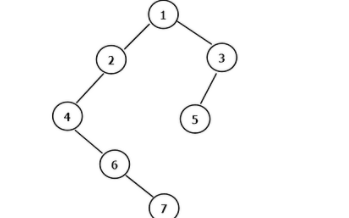
二叉樹(shù)的前序遍歷非遞歸實(shí)現(xiàn)
我們之前說(shuō)了二叉樹(shù)基礎(chǔ)及二叉的幾種遍歷方式及練習(xí)題,今天我們來(lái)看一下二叉樹(shù)的前序遍歷非遞歸實(shí)現(xiàn)。 前序遍歷的順序是, 對(duì)于樹(shù)中的某節(jié)點(diǎn),先遍歷該節(jié)點(diǎn),然后再遍歷其左子樹(shù),最后遍歷其右子
C++基礎(chǔ)語(yǔ)法中的二叉樹(shù)詳解
本期是C++基礎(chǔ)語(yǔ)法分享的第十四節(jié),今天給大家來(lái)梳理一下樹(shù)! ? 二叉樹(shù) BinaryTree.cpp: #include 《stdio.h》#include 《stdlib.h》 #define
C語(yǔ)言數(shù)據(jù)結(jié)構(gòu):什么是二叉樹(shù)?
完全二叉樹(shù):完全二叉樹(shù)是效率很高的數(shù)據(jù)結(jié)構(gòu)。對(duì)于深度為K,有n個(gè)節(jié)點(diǎn)的二叉樹(shù),當(dāng)且僅當(dāng)每一個(gè)節(jié)點(diǎn)都與深度為K的滿(mǎn)二叉樹(shù)中編號(hào)從1至n的節(jié)點(diǎn)一一對(duì)應(yīng)時(shí),稱(chēng)為完全
怎么就能構(gòu)造成二叉樹(shù)呢?
一直跟著公眾號(hào)學(xué)算法的錄友 應(yīng)該知道,我在二叉樹(shù):構(gòu)造二叉樹(shù)登場(chǎng)!,已經(jīng)講過(guò),只有 中序與后序 和 中序和前序 可以確定一顆唯一的二叉樹(shù)。前序和后序是不能確定唯一的二叉樹(shù)的。
使用C語(yǔ)言代碼實(shí)現(xiàn)平衡二叉樹(shù)
這篇博客主要總結(jié)平衡二叉樹(shù),所以,二叉排序樹(shù)知識(shí)不會(huì)提及,但是會(huì)用到。
二叉樹(shù)的代碼實(shí)現(xiàn)
二叉樹(shù)的主要操作有遍歷,例如有先序遍歷、中序遍歷、后序遍歷。在遍歷之前,就是創(chuàng)建一棵二叉樹(shù),當(dāng)然,還需要有刪除二叉樹(shù)的算法。
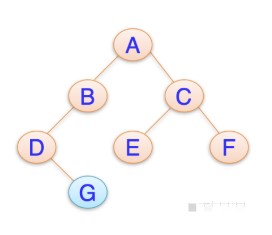





 C++自定義二叉樹(shù)并輸出二叉樹(shù)圖形
C++自定義二叉樹(shù)并輸出二叉樹(shù)圖形










評(píng)論