我們之前說(shuō)了二叉樹(shù)基礎(chǔ)及二叉的幾種遍歷方式及練習(xí)題,今天我們來(lái)看一下二叉樹(shù)的前序遍歷非遞歸實(shí)現(xiàn)。
前序遍歷的順序是, 對(duì)于樹(shù)中的某節(jié)點(diǎn),先遍歷該節(jié)點(diǎn),然后再遍歷其左子樹(shù),最后遍歷其右子樹(shù)。
我們先來(lái)通過(guò)下面這個(gè)動(dòng)畫(huà)復(fù)習(xí)一下二叉樹(shù)的前序遍歷。
迭代遍歷
我們?cè)囅胍幌拢拔覀兘柚?duì)列幫我們實(shí)現(xiàn)二叉樹(shù)的層序遍歷,
那么可不可以,也借助數(shù)據(jù)結(jié)構(gòu),幫助我們實(shí)現(xiàn)二叉樹(shù)的前序遍歷。
假設(shè)我們的二叉樹(shù)為 [1,2,3]。我們需要對(duì)其進(jìn)行前序遍歷。其遍歷順序?yàn)?/p>
當(dāng)前節(jié)點(diǎn) 1,左孩子 2,右孩子 3。
這里可不可以用棧,幫我們完成前序遍歷呢?
棧和隊(duì)列的那些事
我們都知道棧的特性是先進(jìn)后出,我們借助棧來(lái)幫助我們完成前序遍歷的時(shí)候。
則需要注意的一點(diǎn)是,我們應(yīng)該先將右子節(jié)點(diǎn)入棧,再將左子節(jié)點(diǎn)入棧。
這樣出棧時(shí),則會(huì)先出左節(jié)點(diǎn),再出右子節(jié)點(diǎn),則能夠完成樹(shù)的前序遍歷。
我們用一句話對(duì)上圖進(jìn)行總結(jié),當(dāng)棧不為空時(shí),棧頂元素出棧,如果其右孩子不為空,則右孩子入棧,其左孩子不為空,則左孩子入棧。還有一點(diǎn)需要注意的是,我們和層序遍歷一樣,需要先將 root 節(jié)點(diǎn)進(jìn)行入棧,然后再執(zhí)行 while 循環(huán)。
看到這里你已經(jīng)能夠自己編寫(xiě)出代碼了,不信你去試試。
時(shí)間復(fù)雜度:O(n) 需要對(duì)所有節(jié)點(diǎn)遍歷一次
空間復(fù)雜度:O(n) 棧的開(kāi)銷(xiāo),平均為 O(logn) 最快情況,即斜二叉樹(shù)時(shí)為 O(n)
參考代碼
class Solution {
public List《Integer》 preorderTraversal(TreeNode root) {
List《Integer》 list = new ArrayList《》();
Stack《TreeNode》 stack = new Stack《》();
if (root == null) return list;
stack.push(root);
while (!stack.isEmpty()) {
TreeNode temp = stack.pop();
if (temp.right != null) {
stack.push(temp.right);
}
if (temp.left != null) {
stack.push(temp.left);
}
//這里也可以放到前面
list.add(temp.val);
}
return list;
}
}
Morris
Morris 遍歷利用樹(shù)的左右孩子為空(大量空閑指針),實(shí)現(xiàn)空間開(kāi)銷(xiāo)的極限縮減。這個(gè)遍歷方式,稍微有那么一丟丟難理解,不過(guò)結(jié)合動(dòng)圖,也就一目了然,下面我們先看動(dòng)畫(huà)吧。
看完視頻,是不是感覺(jué)自己搞懂了,又感覺(jué)自己沒(méi)搞懂,哈哈,咱們繼續(xù)往下看。
我們之前說(shuō)的,Morris 遍歷利用了樹(shù)中大量空閑指針的特性,我們需要找到當(dāng)前節(jié)點(diǎn)的左子樹(shù)中的最右邊的葉子節(jié)點(diǎn),將該葉子節(jié)點(diǎn)的 right 指向當(dāng)前節(jié)點(diǎn)。例如當(dāng)前節(jié)點(diǎn)為2,其左子樹(shù)中的最右節(jié)點(diǎn)為 9 ,則在 9 節(jié)點(diǎn)添加一個(gè) right 指針指向 2。
其實(shí)上圖中的 Morris 遍歷遵循兩個(gè)原則,我們?cè)趧?dòng)畫(huà)中也能夠得出。
1.當(dāng) p1.left == null 時(shí),p1 = p1.right。(這也就是我們?yōu)槭裁匆o葉子節(jié)點(diǎn)添加 right 指針的原因)
2.如果 p1.left != null,找到 p1 左子樹(shù)上最右的節(jié)點(diǎn)。(也就是我們的 p2 最后停留的位置),此時(shí)我們又可以分為兩種情況,一種是葉子節(jié)點(diǎn)添加 right 指針的情況,一種是去除葉子節(jié)點(diǎn) right 指針的情況。
如果 p2 的 right 指針指向空,讓其指向 p1,p1向左移動(dòng),即 p1 = p1.left
如果 p2 的 right 指針指向 p1,讓其指向空,(為了防止重復(fù)執(zhí)行,則需要去掉 right 指針)p1 向右移動(dòng),p1 = p1.right。
這時(shí)你可以結(jié)合咱們剛才提到的兩個(gè)原則,再去看一遍動(dòng)畫(huà),并代入規(guī)則進(jìn)行模擬,差不多就能完全搞懂啦。
下面我們來(lái)對(duì)動(dòng)畫(huà)中的內(nèi)容進(jìn)行拆解 ,
首先 p1 指向 root節(jié)點(diǎn)
p2 = p1.left,下面我們需要通過(guò) p2 找到 p1的左子樹(shù)中的最右節(jié)點(diǎn)。即節(jié)點(diǎn) 5,然后將該節(jié)點(diǎn)的 right 指針指向 root。并記錄 root 節(jié)點(diǎn)的值。
向左移動(dòng) p1,即 p1 = p1.left
p2 = p1.left ,即節(jié)點(diǎn) 4 ,找到 p1 的左子樹(shù)中的最右葉子節(jié)點(diǎn),也就是 9,并將該節(jié)點(diǎn)的 right 指針指向 2。
繼續(xù)向左移動(dòng) p1,即 p1 = p1.left,p2 = p1.left。也就是節(jié)點(diǎn) 8。并將該節(jié)點(diǎn)的 right 指針指向 p1。
我們發(fā)現(xiàn)這一步給前兩步是一樣的,都是找到葉子節(jié)點(diǎn),將其 right 指針指向 p1,此時(shí)我們完成了添加 right 指針的過(guò)程,下面我們繼續(xù)往下看。
我們繼續(xù)移動(dòng) p1 指針,p1 = p1.left。p2 = p.left。此時(shí)我們發(fā)現(xiàn) p2 == null,即下圖此時(shí)我們需要移動(dòng) p1, 但是不再是 p1 = p1.left 而是 p1 = p1.right。也就是 4,繼續(xù)讓 p2 = p1.left。此時(shí)則為下圖這種情況
此時(shí)我們發(fā)現(xiàn) p2.right != null 而是指向 4,說(shuō)明此時(shí)我們已經(jīng)添加過(guò)了 right 指針,所以去掉 right 指針,并讓 p1 = p1.right
下面則繼續(xù)移動(dòng) p1 ,按照規(guī)則繼續(xù)移動(dòng)即可,遇到的情況已經(jīng)在上面做出了舉例,所以下面我們就不繼續(xù)贅述啦,如果還不是特別理解的同學(xué),可以再去看一遍動(dòng)畫(huà)加深下印象。時(shí)間復(fù)雜度 O(n),空間復(fù)雜度 O(1)下面我們來(lái)看代碼吧。
代碼
class Solution {
public List《Integer》 preorderTraversal(TreeNode root) {
List《Integer》 list = new ArrayList《》();
if (root == null) {
return list;
}
TreeNode p1 = root; TreeNode p2 = null;
while (p1 != null) {
p2 = p1.left;
if (p2 != null) {
//找到左子樹(shù)的最右葉子節(jié)點(diǎn)
while (p2.right != null && p2.right != p1) {
p2 = p2.right;
}
//添加 right 指針,對(duì)應(yīng) right 指針為 null 的情況
if (p2.right == null) {
list.add(p1.val);
p2.right = p1;
p1 = p1.left;
continue;
}
//對(duì)應(yīng) right 指針存在的情況,則去掉 right 指針
p2.right = null;
} else {
list.add(p1.val);
}
//移動(dòng) p1
p1 = p1.right;
}
return list;
}
}
原文標(biāo)題:把二叉樹(shù)揉碎(二)
文章出處:【微信公眾號(hào):算法與數(shù)據(jù)結(jié)構(gòu)】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
責(zé)任編輯:haq
-
二叉樹(shù)
+關(guān)注
關(guān)注
0文章
74瀏覽量
12636
原文標(biāo)題:把二叉樹(shù)揉碎(二)
文章出處:【微信號(hào):TheAlgorithm,微信公眾號(hào):算法與數(shù)據(jù)結(jié)構(gòu)】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
億緯鋰能榮獲杭叉集團(tuán)2022-2024年度優(yōu)秀供應(yīng)商獎(jiǎng)
想在rtsmart中使用uart2,是不是只能通過(guò)修改設(shè)備樹(shù)方法來(lái)實(shí)現(xiàn)uart2的復(fù)用呀?
機(jī)器人看點(diǎn):宇樹(shù)科技王興興回上海母校 加速商業(yè)化落地 宇樹(shù)機(jī)器人二手租賃火爆
求解答,設(shè)備樹(shù)問(wèn)題
宇樹(shù)科技在物聯(lián)網(wǎng)方面
嵌入式學(xué)習(xí)-飛凌嵌入式ElfBoard ELF 1板卡-初識(shí)設(shè)備樹(shù)之設(shè)備樹(shù)組成和結(jié)構(gòu)
字符串反轉(zhuǎn)的實(shí)現(xiàn)方式
飛凌嵌入式ElfBoard ELF 1板卡-初識(shí)設(shè)備樹(shù)之設(shè)備樹(shù)組成和結(jié)構(gòu)
一千余字解讀stm32時(shí)鐘樹(shù)

ATA-2041高壓放大器在叉指形電極管狀壓電元件電極制備中的應(yīng)用

dp接口的最新技術(shù)發(fā)展
鐳神智能機(jī)器人三向叉式3D SLAM無(wú)人叉車(chē):重塑高位堆垛與窄通道倉(cāng)儲(chǔ)新境界

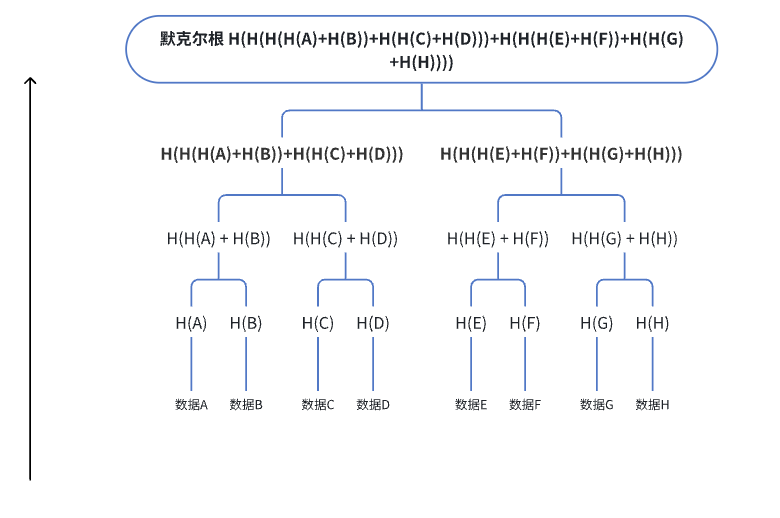
什么是默克爾樹(shù)(Merkle Tree)?如何計(jì)算默克爾根?
【北京迅為】iTOP-i.MX6開(kāi)發(fā)板使用手冊(cè)第四部分固件編譯第十四章非設(shè)備樹(shù)Android4.4系統(tǒng)編譯






 二叉樹(shù)的前序遍歷非遞歸實(shí)現(xiàn)
二叉樹(shù)的前序遍歷非遞歸實(shí)現(xiàn)











評(píng)論