深度學(xué)習(xí)的熱潮還在不斷涌動,神經(jīng)網(wǎng)絡(luò)再次成為業(yè)界人士特別關(guān)注的問題,AI 的未來大有可期,而深度學(xué)習(xí)正在影響我們的日常生活。近日斯坦福大學(xué)給我們分享咯一則他對深度神經(jīng)網(wǎng)絡(luò)可解釋性的探索的論文,我們?nèi)タ纯此侨缋斫獾陌桑?/p>
近日,斯坦福大學(xué)計算機科學(xué)博士生 Mike Wu 發(fā)表博客介紹了他對深度神經(jīng)網(wǎng)絡(luò)可解釋性的探索,主要提到了樹正則化。其論文《Beyond Sparsity: Tree Regularization of Deep Models for Interpretability》已被 AAAI 2018 接收。
近年來,深度學(xué)習(xí)迅速成為業(yè)界、學(xué)界的重要工具。神經(jīng)網(wǎng)絡(luò)再次成為解決圖像識別、語音識別、文本翻譯以及其他困難問題的先進技術(shù)。去年十月,Deepmind 發(fā)布了 AlphaGo 的更強版本,從頭開始訓(xùn)練即可打敗最優(yōu)秀的人類選手和機器人,表明 AI 的未來大有可期。在業(yè)界,F(xiàn)acebook、谷歌等公司將深度網(wǎng)絡(luò)集成在計算 pipeline 中,從而依賴算法處理每天數(shù)十億比特的數(shù)據(jù)。創(chuàng)業(yè)公司,如 Spring、Babylon Health 正在使用類似的方法來顛覆醫(yī)療領(lǐng)域。深度學(xué)習(xí)正在影響我們的日常生活。
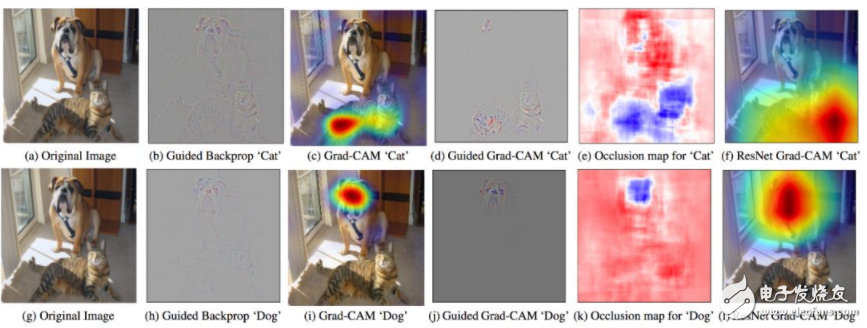
圖 1:GradCam - 利用目標(biāo)概念的梯度突出重要像素,從而創(chuàng)建決策的視覺解釋。
但是深度學(xué)習(xí)是一個黑箱。我第一次聽說它時,就對其工作原理非常費解。幾年過去了,我仍然在探索合理的答案。嘗試解釋現(xiàn)代神經(jīng)網(wǎng)絡(luò)很難,但是至關(guān)重要。如果我們打算依賴深度學(xué)習(xí)制造新的 AI、處理敏感的用戶數(shù)據(jù),或者開藥,那么我們必須理解這些模型的工作原理。
很幸運,學(xué)界人士也提出了很多對深度學(xué)習(xí)的理解。以下是幾個近期論文示例:
Grad-Cam(Selvaraju et. al. 2017):使用最后卷積層的梯度生成熱力圖,突出顯示輸入圖像中的重要像素用于分類。
LIME(Ribeiro et. al. 2016):使用稀疏線性模型(可輕松識別重要特征)逼近 DNN 的預(yù)測。
特征可視化(Olah 2017):對于帶有隨機噪聲的圖像,優(yōu)化像素來激活訓(xùn)練的 DNN 中的特定神經(jīng)元,進而可視化神經(jīng)元學(xué)到的內(nèi)容。
Loss Landscape(Li et. al. 2017):可視化 DNN 嘗試最小化的非凸損失函數(shù),查看架構(gòu)/參數(shù)如何影響損失情況。

圖 2:特征可視化:通過優(yōu)化激活特定神經(jīng)元或一組神經(jīng)元,從而生成圖像(Olah 2017)。
從上述示例中可見,學(xué)界對如何解釋 DNN 存在不同見解。隔離單個神經(jīng)元的影響?可視化損失情況?特征稀疏性?
什么是可解釋性?
我們應(yīng)該把可解釋性看作人類模仿性(human simulatability)。如果人類可以在合適時間內(nèi)采用輸入數(shù)據(jù)和模型參數(shù),經(jīng)過每個計算步,作出預(yù)測,則該模型具備模仿性(Lipton 2016)。
這是一個嚴(yán)格但權(quán)威的定義。以醫(yī)院生態(tài)系統(tǒng)為例:給定一個模仿性模型,醫(yī)生可以輕松檢查模型的每一步是否違背其專業(yè)知識,甚至推斷數(shù)據(jù)中的公平性和系統(tǒng)偏差等。這可以幫助從業(yè)者利用正向反饋循環(huán)改進模型。
決策樹具備模仿性
我們可以很輕松地看到?jīng)Q策樹具備模仿性。例如,如果我想預(yù)測病人心臟病發(fā)作的風(fēng)險,我可以沿著決策樹的每個節(jié)點走下去,理解哪些特征可用于作出預(yù)測。
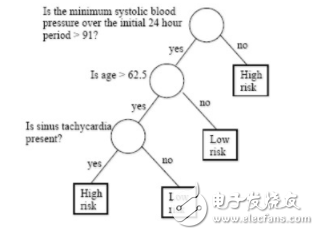
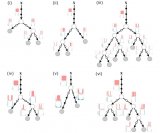
圖 3:訓(xùn)練用于分類心臟病發(fā)作風(fēng)險的決策樹。這棵樹最大路徑長度為 3。
如果我們可以使用決策樹代替 DNN,那么已經(jīng)完成了。但是使用 DNN 盡管缺乏可解釋性,但是它的能力遠超過決策樹。所以我們是否可以將決策樹和 DNN 結(jié)合起來,構(gòu)架具備模仿性的強大模型?
我們可以試著做一個類似 LIME 的東西,構(gòu)建一個模擬決策樹來逼近訓(xùn)練后的 DNN 的預(yù)測結(jié)果。但是訓(xùn)練深度神經(jīng)網(wǎng)絡(luò)時會出現(xiàn)很多局部極小值,其中只有部分極小值容易模仿。因此,用這種方法可能最后會陷于一個難以模仿的極小值(生成一個巨型決策樹,無法在合理時間內(nèi)走完)。
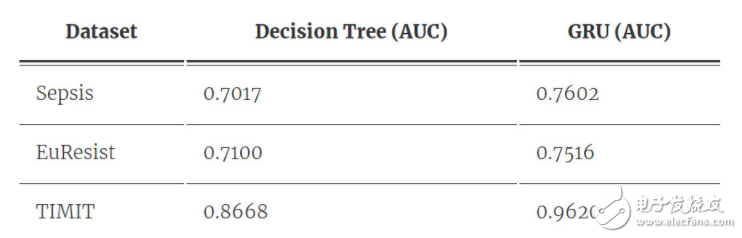
表 1:決策樹和 RNN 在不同數(shù)據(jù)集上的性能。我們注意到 RNN 的預(yù)測能力比決策樹優(yōu)秀許多。
直接優(yōu)化提高模仿性
如果我們想在優(yōu)化過程中提高模仿性,則可以嘗試找到更具可解釋性的極小值。完美情況是,我們訓(xùn)練一個行為非常像(但并不是)決策樹的 DNN,因為我們?nèi)匀幌肜蒙窠?jīng)網(wǎng)絡(luò)的非線性。
另一種方式是使用簡單決策樹正則化深度神經(jīng)網(wǎng)絡(luò)。我們稱之為樹正則化。
樹正則化
若我們有包含 N 個序列的時序數(shù)據(jù)集,每一個序列有 T_n 個時間步。當(dāng)沒有限制時,我們可以假設(shè)它有二元輸出。一般傳統(tǒng)上,訓(xùn)練循環(huán)神經(jīng)網(wǎng)絡(luò)(RNN)可以使用以下?lián)p失函數(shù):
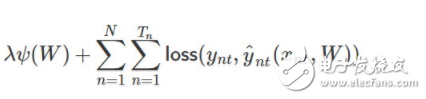
其中ψ為正則化器(即 L1 或 L2 正則化)、λ 為正則化系數(shù)或強度、W 為一組 RNN 的權(quán)重矩陣、y_nt 為單個時間步上的標(biāo)注真值、y_nt hat 為單個時間步上的預(yù)測值。此外,損失函數(shù)一般可以選為交叉熵損失函數(shù)。
添加樹正則化需要改變兩個地方。第一部分是給定一些帶權(quán)重 W 的 RNN,且權(quán)重 W 可以是部分已訓(xùn)練的,我們將 N 個長度為 T 的數(shù)據(jù) X 傳遞到 RNN 中以執(zhí)行預(yù)測。然后我們就能使用這 N 個數(shù)據(jù)對訓(xùn)練決策樹算法,并嘗試匹配 RNN 的預(yù)測。

圖 4:在優(yōu)化過程中的任意點,我們能通過一個簡單的決策樹逼近部分訓(xùn)練的 DNN。
因此,我們現(xiàn)在有了模擬 DT,但我們可以選擇一個十分小或十分大的決策樹,因此我們需要量化樹的大小。
為了完成量化過程,首先我們需要考慮樹的平均路徑長度(APL)。對于單個樣本,路徑長度就等于游歷樹并作出預(yù)測的長度。例如,如圖 3 所示,若有一個用來預(yù)測心臟病的決策樹,那么假設(shè)輸入 x 為 age=70。該樣本下路徑長度因為 70》62.5 而等于 2。因此平均路徑長度可以簡單地表示為 ∑ pathlength(x_n, y_n hat)。

圖 5:給定一棵決策樹與數(shù)據(jù)集,我們能計算平均路徑長度以作為模擬、解釋平均樣本的成本。通過把這一項加入到目標(biāo)函數(shù),我們就能鼓勵 DNN 生成簡單的 DT 樹并懲罰復(fù)雜而巨大的決策樹。
因此我們最后能將損失函數(shù)改寫為以下形式:
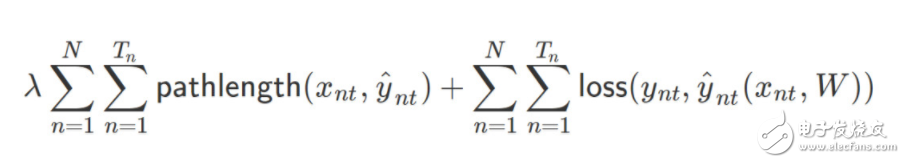
現(xiàn)在只有一個問題:決策樹是不可微的。但我們可能真的比較希望能用 SGD 以實現(xiàn)更快速和便捷的最優(yōu)化,因此我們也許可以考慮更具創(chuàng)造性的方法。
我們可以做的是添加一個代理模型,它可能是一個以 RNN 權(quán)重作為輸入的多層感知機(MLP),并期望能輸出平均路徑長度的估計量,就好像我們在訓(xùn)練一個決策樹一樣。

圖 6:通過使用代理模型,我們可以利用流行的梯度下降算法來訓(xùn)練 DNN。為了訓(xùn)練一個代理模型,我們最小化標(biāo)注真值和預(yù)測 APL 之間的 MSE。
當(dāng)我們優(yōu)化 RNN/DNN 時,每一個梯度下降步都會生成一組新的權(quán)重 W_i。對于每一個 W_i,我們能訓(xùn)練一個決策樹并計算平均路徑長度。在訓(xùn)練幾個 epoch 之后,我們能創(chuàng)建一個大型數(shù)據(jù)集并訓(xùn)練代理 MLP。
訓(xùn)練過程會給定一個固定的代理,我們能定義正則化目標(biāo)函數(shù),并優(yōu)化 RNN。若給定一個固定的 RNN,我們將構(gòu)建一個數(shù)據(jù)集并優(yōu)化 MLP。
小測試數(shù)據(jù)集
檢查新技術(shù)有效性的一個好方法是在合成數(shù)據(jù)及上進行測試,在其中我們可以強調(diào)新技術(shù)提出的效益。
考慮以下的虛構(gòu)數(shù)據(jù)集:給定單位二維坐標(biāo)系統(tǒng)內(nèi)的點 (x_i,y_i),定義一個拋物線決策函數(shù)。
y=5?(x?0.5)^2+0.4
我們在單位正方形 [0,1]×[0,1] 內(nèi)均勻地隨機采樣 500 個點,所有在拋物線之上的點設(shè)為正的,在拋物線之下的點設(shè)為負的。我們通過隨機翻轉(zhuǎn) 10% 的邊界附近(圖 7 的兩條灰色拋物線之間)的點以添加一些噪聲。然后,隨機分離出 30% 的點用作測試集。
我們訓(xùn)練了一個 3 層 MLP 用作分類器,其中第一層有 100 個節(jié)點,第二層有 100 個節(jié)點,第三層有 10 個節(jié)點。我們有意讓該模型過度表達,以使其過擬合,并強調(diào)正則化的作用。
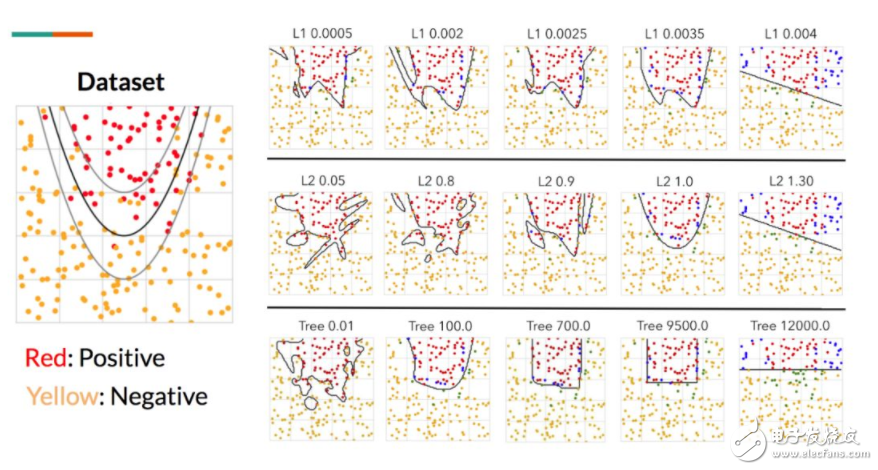
圖 7:虛構(gòu)的拋物線數(shù)據(jù)集。我們訓(xùn)練了一個深度 MLP,結(jié)合不同級別的 L1、L2 正則化和樹正則化以測試最終決策邊界之間的視覺差異。這里的關(guān)鍵之處在于,樹正則化生成了坐標(biāo)對齊的邊界。然后我們用改變的正則化(L1、L2、樹)和改變的強度λ訓(xùn)練了一系列的 MLP。我們可以通過描述單位正方形內(nèi)所有點的行為并畫出等高線以評估模型,從而逼近已學(xué)習(xí)的決策函數(shù)。圖 7 展示了在不同參數(shù)設(shè)置下的已學(xué)習(xí)決策函數(shù)的并行對比。
正如預(yù)期,隨著正則化強度增加,得到的決策函數(shù)也更簡單(減少過擬合)。更重要的是,這三種正則化方法生成不同形狀的決策函數(shù)。L1 正則化傾向于生成凹凸不平的線,L2 正則化傾向于球狀的線,樹正則化傾向于生成坐標(biāo)對齊的決策函數(shù)。這為決策樹的工作方式提供了更多的直覺理解。
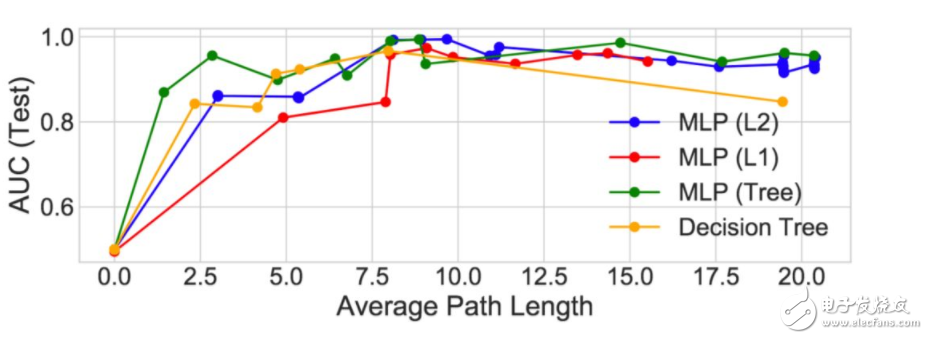
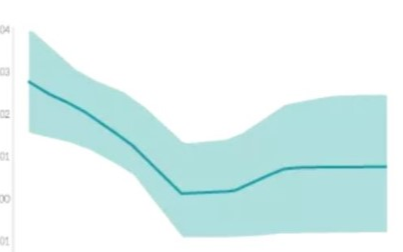
圖 8:正則化模型的 APL 性能對比。這里,決策樹(黃線)是原始的決策樹(沒有 DNN)。我們注意到在 1.0 到 5.0 之間樹正則化 MLP 的性能高于(以及復(fù)雜度低于)所有其它的模型。
至少在這個虛構(gòu)示例中,樹正則化在高度正則化區(qū)域(人類可模擬)能得到更好的性能。例如,樹正則化結(jié)合λ=9500.0 只需要 3 個分支就可以獲得類似拋物線的決策函數(shù)(有更高的 APL)。
真實數(shù)據(jù)集
現(xiàn)在我們對樹正則化有了一個直觀認識,下面就來看一下真實世界數(shù)據(jù)集(帶有二分類結(jié)果),以及樹正則化與 L1、L2 正則化的對比。以下是對數(shù)據(jù)集的簡短描述:
Sepsis(Johnson et. al. 2016):超過 1.1 萬敗血癥 ICU 病人的時序數(shù)據(jù)。我們在每個時間步可以獲取 35 個生命體征的數(shù)據(jù)向量、標(biāo)簽結(jié)果(如含氧量或心率)和 5 個二分類結(jié)果的標(biāo)簽(即是否使用呼吸機或是否死亡)。
EuResist(Zazzi et. al. 2012):5 萬 HIV 病人的時序數(shù)據(jù)。該結(jié)構(gòu)非常類似于 Sepsis,不過它包括 40 個輸入特征和 15 個輸出特征。
TIMIT(Garofolo et. al. 1993):630 位英語說話人的錄音,每個語句包括 60 個音素。我們專注于區(qū)分阻塞音(如 b、g)和非阻塞音。輸入特征是連續(xù)聲系數(shù)和導(dǎo)數(shù)。
我們對真實世界數(shù)據(jù)集進行虛擬數(shù)據(jù)集同樣的操作,除了這次我們訓(xùn)練的是 GRU-RNN。我們再次用不同的正則化執(zhí)行一系列實驗,現(xiàn)在還利用針對 GRU 的不同隱藏單元大小進行實驗。
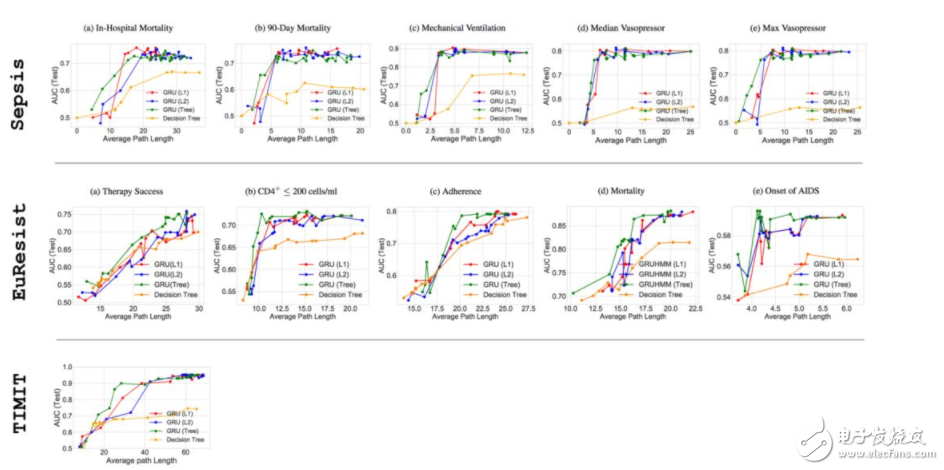
圖 9:正則化模型在 Sepsis(5/5 輸出維度)、EuResist (5/15 輸出維度)和 TIMIT 的 APL 上的性能對比。可以看到在 APL 較小時,性能與圖 8 類似,樹正則化達到更高的性能。更多詳細結(jié)果和討論見論文 https://arxiv.org/pdf/1711.06178.pdf。
即使在帶有噪聲的真實世界數(shù)據(jù)集中,我們?nèi)匀豢梢钥吹綐湔齽t化在小型 APL 區(qū)域中優(yōu)于 L1 和 L2 正則化。我們尤其關(guān)注這些低復(fù)雜度的「甜蜜點」(sweet spot),因為這就是深度學(xué)習(xí)模型模仿性所在,也是在醫(yī)療、法律等注重安全的環(huán)境中實際有用之處。
此外,我們已經(jīng)訓(xùn)練了一個樹正則化 DNN,還可以訓(xùn)練一個模仿性決策樹查看最終的決策樹是什么樣子。這是一次很好的完整性檢查,因為我們期望模仿性決策樹具備模仿性,且與特定問題領(lǐng)域相關(guān)。
下圖展示了針對 Sepsis 中 2 個輸出維度的模仿性決策樹。由于我們不是醫(yī)生,因此我們請一位敗血癥治療專家檢查這些樹。
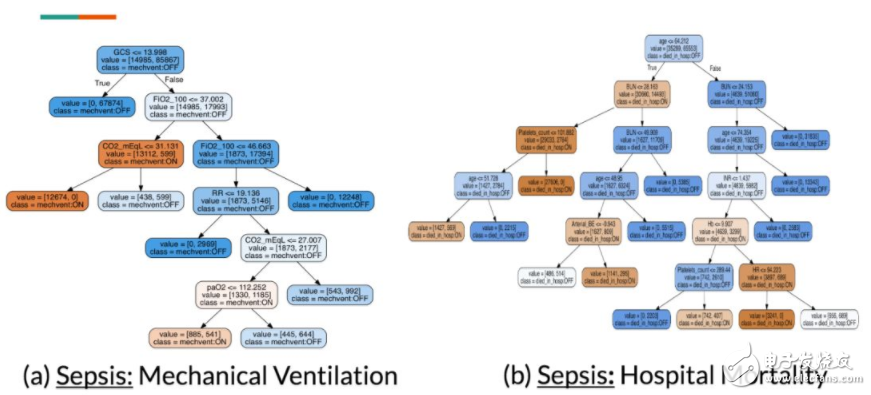
圖 10:構(gòu)建決策樹以仿真已訓(xùn)練的樹正則化 DNN(包含 Sepsis 的 5 個維度中的兩個)。從視覺上,我們可以確認這些樹的 APL 值較小,并且是可模仿的。
考慮 mechanical ventilation 決策樹,臨床醫(yī)生注意到樹節(jié)點上的特征(FiO2、RR、CO2 和 paO2)以及中斷點上的值是醫(yī)學(xué)上有效的,這些特征都是測量呼吸質(zhì)量的。
對于 hospital mortality 決策樹,他注意到該決策樹上的一些明顯的矛盾:有些無器官衰竭的年輕病人被預(yù)測為高死亡率,而其他的有器官衰竭的年輕病人卻被預(yù)測為低死亡率。然后臨床醫(yī)生開始思考,未捕獲的(潛在的)變量如何影響決策樹過程。而這種思考過程不可能通過對深度模型的簡單敏感度分析而進行。
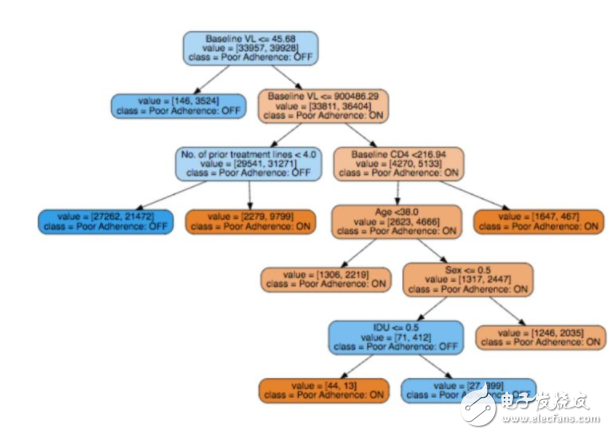
圖 11:和圖 10 相同,但是是從 EuResist 數(shù)據(jù)集的其中一個輸出維度(服藥堅持性)。
為了把事情做到底,我們可以看看一個嘗試解釋病人不能服從 HIV 藥物處方(EuResist)的原因的決策樹。我們再次咨詢了臨床醫(yī)生,他確認出,基礎(chǔ)病毒量(baseline viral load)和事先治療線(prior treatment line)是決策樹中的重要屬性,是有用的決策變量。多項研究(Langford, Ananworanich, and Cooper 2007, Socas et. al. 2011)表明高基線的病毒量會導(dǎo)致更快的病情惡化,因此需要多種藥物雞尾酒療法,太多的處方使得病人更難遵從醫(yī)囑。
可解釋性優(yōu)先
本文的重點是一種鼓勵復(fù)雜模型在不犧牲太多預(yù)測性能的前提下,逼近人類模仿性功能的技術(shù)。我認為這種可解釋性非常強大,可以允許領(lǐng)域?qū)<依斫夂徒朴嬎愫谙淠P驼谧龅氖虑椤?/p>
AI 安全逐漸成為主流。很多會議如 NIPS 開始更多關(guān)注現(xiàn)代機器學(xué)習(xí)中的公平性、可解釋性等重要問題。之前我們認真地將深度學(xué)習(xí)應(yīng)用于消費者產(chǎn)品和服務(wù)(自動駕駛汽車),我們確實需要更好地了解這些模型的工作原理。這意味著我們需要開發(fā)更多可解釋性示例(人類專家參與其中)。
Notes:本文將會出現(xiàn)在 AAAI 2018 上(Beyond Sparsity: Tree Regularization of Deep Models for Interpretability),預(yù)印版可在 arXiv 上找到:https://arxiv.org/abs/1711.06178。類似的版本已經(jīng)在 NIP 2017 上進行了 oral 解讀。
問答
代理 MLP 追蹤 APL 表現(xiàn)如何?
讓人吃驚地好。在所有實驗中,我們使用帶有 25 個隱藏節(jié)點的單層 MLP(這是相當(dāng)小的一個網(wǎng)絡(luò))。這必須有一個預(yù)測 APL 權(quán)重的低維表征。
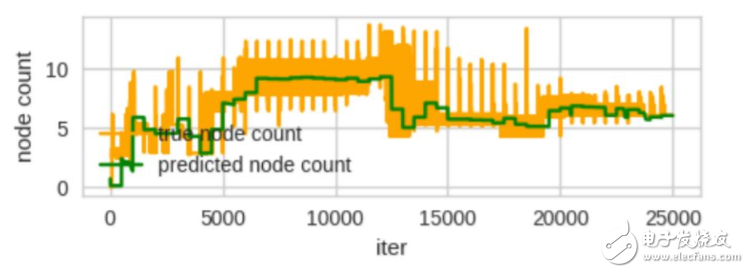
圖 12:真節(jié)點計數(shù)指的是真正訓(xùn)練決策樹并計算 APL。已預(yù)測的節(jié)點計數(shù)指的是代理 MLP 的輸出。
與原決策樹相比,樹正則化模型的表現(xiàn)如何?
上述的每個對比圖展示了與正則 DNN 對比的決策樹 AUCs。為了生成這些線,我們在不同決策樹超參數(shù)(即定義葉、基尼系數(shù)等的最小樣本數(shù))上進行了網(wǎng)格搜索。我們注意到在所有案例中,DT 表現(xiàn)要比所有正則化方法更差。這表明樹正則化不能只復(fù)制 DT。
文獻中有與此相似的嗎?
除了在文章開頭提及的相關(guān)工作,模型提取/壓縮很可能是最相似的子領(lǐng)域。其主要思想是訓(xùn)練一個更小模型以模擬一個更深網(wǎng)絡(luò)。這里,我們主要在優(yōu)化中使用 DT 執(zhí)行提取。
樹正則化的運行時間如何?
讓我們看一下 TIMIT 數(shù)據(jù)集(最大的數(shù)據(jù)集)。L2 正則化 GRU 每 epoch 用時 2116 秒。帶有 10 個狀態(tài)的樹正則化 GRU 每個 epoch 用時 3977 秒,這其中包含訓(xùn)練代理的時間。實際上,我們做的非常謹(jǐn)慎。例如,如果我們每 25 個 epoch 做一次,我們將獲得 2191 秒的一個平均的每 epoch 的成本。
在多個運行中,(最后的)模擬 DT 穩(wěn)定嗎?
如果樹正則化強大(高λ),最終的 DT 在不同運行中是穩(wěn)定的(頂多在一些節(jié)點上不同)。
DT 對深度模型的預(yù)測有多準(zhǔn)確?
換言之,這一問題是在問如果訓(xùn)練期間 DT 的預(yù)測與 DNN 預(yù)測是否密切匹配。如果沒有,那么我們無法有效地真正正則化我們的模型。但是我們并不希望匹配很精確。
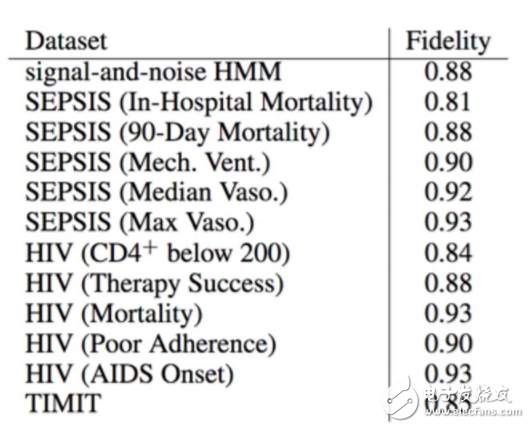
在上表中,我們測量了保真度(Craven and Shavlik 1996),這是 DT 預(yù)測與 DNN 一致的測試實例的百分比。因此 DT 是準(zhǔn)確的。
殘差 GRU-HMM 模型
(本節(jié)討論一個專為可解釋性設(shè)計的新模型。)
隱馬爾可夫模型(HMM)就像隨機 RNN,它建模潛在變量序列 [z1,…,zT],其中每個潛在變量是 K 離散狀態(tài)之一: z_t∈1,?,K。狀態(tài)序列通常用于生成數(shù)據(jù) x_t,并在每個時間步上輸出觀察到的 y_t。值得注意的是,它包含轉(zhuǎn)化矩陣 A,其中 A_ij=Pr(z_t=i|z_t?1=j),以及一些產(chǎn)生數(shù)據(jù)的發(fā)射參數(shù)。HMMs 通常被認為是一個更可闡釋的模型,因為聚類數(shù)據(jù)的 K 潛在變量通常在語義上是有意義的。
當(dāng)使用 HMM 潛在狀態(tài)(換言之,當(dāng) HMM 捕獲數(shù)據(jù)不足時,只使用 GRU)預(yù)測二值目標(biāo)之時,我們把 GRU-HMM 定義為一個可以建模殘差誤差的 GRU。根據(jù)殘差模型的性質(zhì),我們可以使用樹正則化只懲罰 GRU 輸出節(jié)點的復(fù)雜性,從而使得 HMM 不受限制。
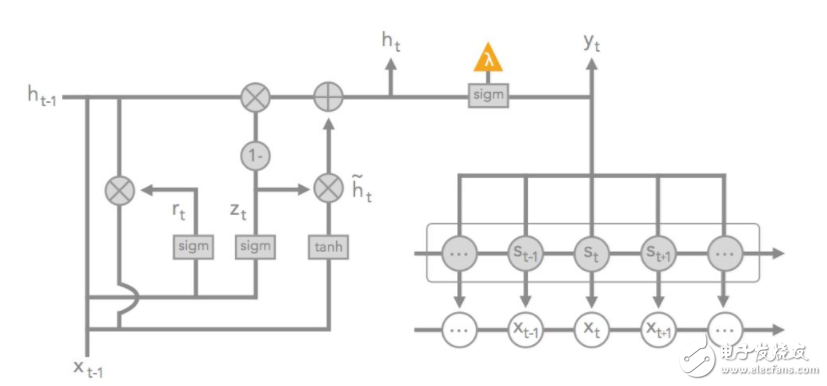
圖 13:GRU-HMM 圖解。x_t 表征時間步 t 上的輸入數(shù)據(jù)。s_t 表征時間步 t 的潛在狀態(tài);r_t,h_t,h_t tilde,z_t 表征 GRU 的變量。最后的 sigmoid(緊挨著橘色三角形)投射在 HMM 狀態(tài)和 GRU 潛在狀態(tài)的總和之上。橘色三角形表示用于樹正則化的替代訓(xùn)練的輸出。
總體而言,深度殘差模型比帶有大體相同參數(shù)的 GRU-only 模型的表現(xiàn)要好 1%。參見論文附錄獲得更多信息。
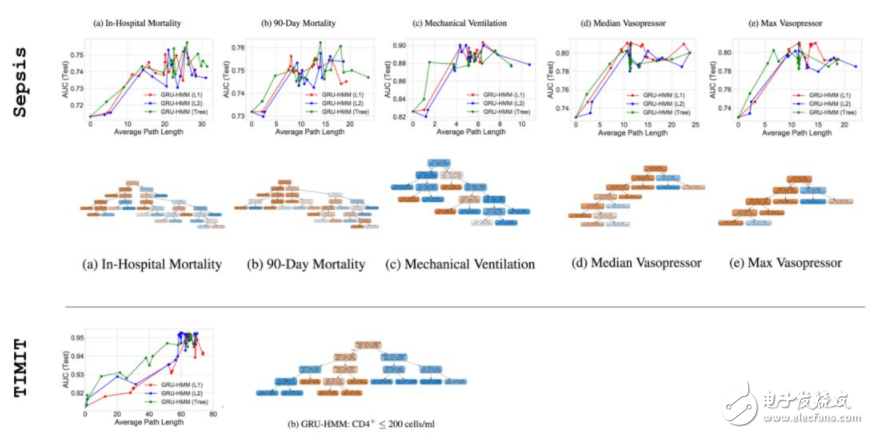
圖 14:就像從前,我們可以為這些殘差模型繪圖并可視化模擬 DT。盡管我們看到相似的「sweet spot」行為,我們注意到最后得到的樹有清晰的結(jié)構(gòu),這表明 GRU 在這一殘差設(shè)置中表現(xiàn)不同。
 電子發(fā)燒友App
電子發(fā)燒友App















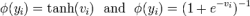












評論