上一次我們用了單隱層的神經(jīng)網(wǎng)絡(luò)，效果還可以改善，這一次就使用CNN。

卷積神經(jīng)網(wǎng)絡(luò)

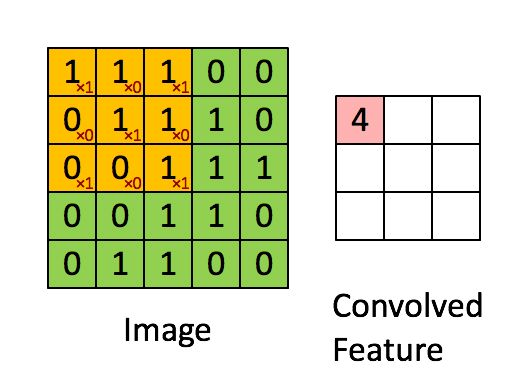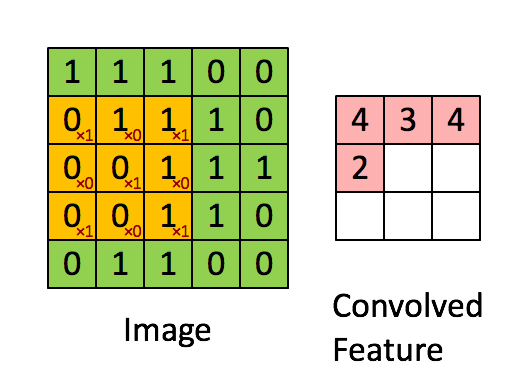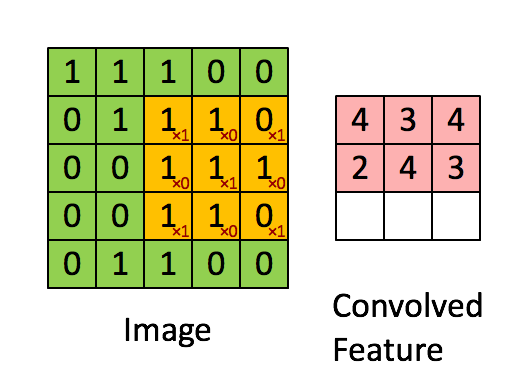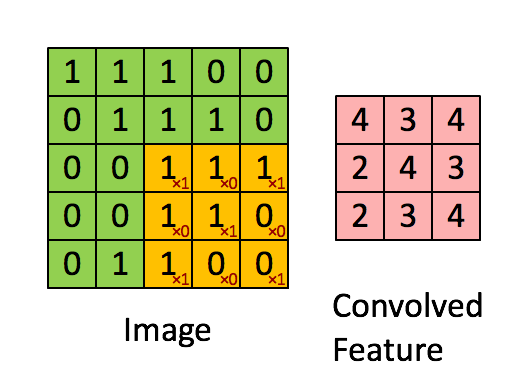
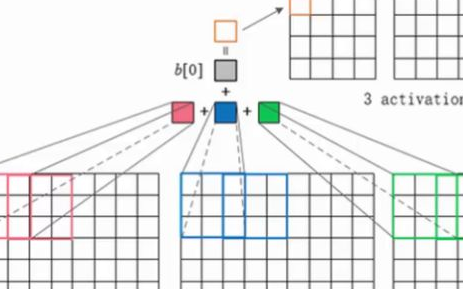
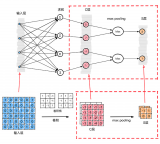
上圖演示了卷積操作

LeNet-5式的卷積神經(jīng)網(wǎng)絡(luò)，是計算機視覺領(lǐng)域近期取得的巨大突破的核心。卷積層和之前的全連接層不同，采用了一些技巧來避免過多的參數(shù)個數(shù)，但保持了模型的描述能力。這些技巧是：
1， 局部聯(lián)結(jié)：神經(jīng)元僅僅聯(lián)結(jié)前一層神經(jīng)元的一小部分。
2， 權(quán)重共享：在卷積層，神經(jīng)元子集之間的權(quán)重是共享的。（這些神經(jīng)元的形式被稱為特征圖[feature map]）
3， 池化：對輸入進行靜態(tài)的子采樣。

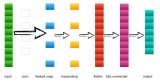
局部性和權(quán)重共享的圖示

卷積層的單元實際上連接了前一層神經(jīng)元中的一個2維patch，這個前提讓網(wǎng)絡(luò)利用了輸入中的2維結(jié)構(gòu)。

當(dāng)使用Lasagne中的卷積層時，我們必須進行一些輸入準(zhǔn)備。輸入不再像剛剛一樣是一個9216像素強度的扁平向量，而是一個有著(c,0,1)形式的三維矩陣，其中c代表通道（顏色），0和1對應(yīng)著圖像的x和y維度。在我們的問題中，具體的三維矩陣為(1,96,96)，因為我們僅僅使用了灰度一個顏色通道。

一個函數(shù)load2d對前述的load函數(shù)進行了包裝，完成這個2維到三維的轉(zhuǎn)變：
def load2d(test=False, cols=None):
X, y = load(test=test)
X = X.reshape(-1, 1, 96, 96)
return X, y

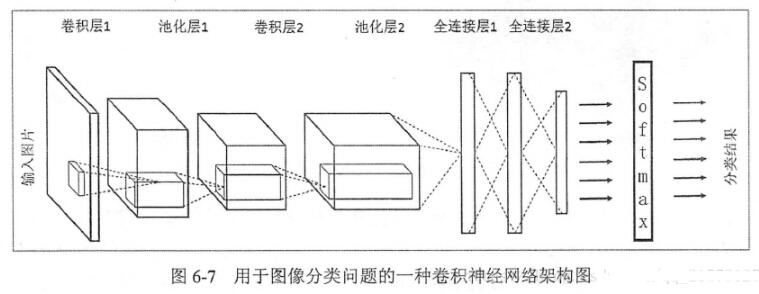
我們將要創(chuàng)建一個具有三個卷積層和兩個全連接層的卷積神經(jīng)網(wǎng)絡(luò)。每個卷積層都跟著一個2*2的最大化池化層。初始卷積層有32個filter，之后每個卷積層我們把filter的數(shù)量翻番。全連接的隱層包含500個神經(jīng)元。

這里還是一樣沒有任何形式（懲罰權(quán)重或者dropout）的正則化。事實證明當(dāng)我們使用尺寸非常小的filter，如3*3或2*2，已經(jīng)起到了非常不錯的正則化效果。

代碼如下：
net2 = NeuralNet(
layers=[
('input', layers.InputLayer),
('conv1', layers.Conv2DLayer),
('pool1', layers.MaxPool2DLayer),
('conv2', layers.Conv2DLayer),
('pool2', layers.MaxPool2DLayer),
('conv3', layers.Conv2DLayer),
('pool3', layers.MaxPool2DLayer),
('hidden4', layers.DenseLayer),
('hidden5', layers.DenseLayer),
('output', layers.DenseLayer),
],
input_shape=(None, 1, 96, 96),
conv1_num_filters=32, conv1_filter_size=(3, 3), pool1_pool_size=(2, 2),
conv2_num_filters=64, conv2_filter_size=(2, 2), pool2_pool_size=(2, 2),
conv3_num_filters=128, conv3_filter_size=(2, 2), pool3_pool_size=(2, 2),
hidden4_num_units=500, hidden5_num_units=500,
output_num_units=30, output_nonlinearity=None,

update_learning_rate=0.01,
update_momentum=0.9,

regression=True,
max_epochs=1000,
verbose=1,
)

X, y = load2d() # load 2-d data
net2.fit(X, y)

# Training for 1000 epochs will take a while. We'll pickle the
# trained model so that we can load it back later:
import cPickle as pickle
with open('net2.pickle', 'wb') as f:
pickle.dump(net2, f, -1)

訓(xùn)練這個網(wǎng)絡(luò)和第一個網(wǎng)絡(luò)相比，將要耗費巨大的時空資源。每次迭代要慢15倍，整個1000次迭代下來要耗費20多分鐘的時間，這還是在你有一個相當(dāng)不錯的GPU的基礎(chǔ)上。

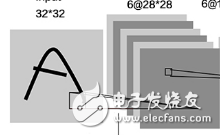
然而耐心總是得到回饋，我們的模型和結(jié)果自然比剛剛好得多。讓我們來看一看運行腳本時的輸出。首先是輸出形狀的層列表，注意因為我們選擇的窗口尺寸，第一個卷積層的32個filter輸出了32張94*94 的特征圖。
InputLayer (None, 1, 96, 96) produces 9216 outputs
Conv2DCCLayer (None, 32, 94, 94) produces 282752 outputs
MaxPool2DCCLayer (None, 32, 47, 47) produces 70688 outputs
Conv2DCCLayer (None, 64, 46, 46) produces 135424 outputs
MaxPool2DCCLayer (None, 64, 23, 23) produces 33856 outputs
Conv2DCCLayer (None, 128, 22, 22) produces 61952 outputs
MaxPool2DCCLayer (None, 128, 11, 11) produces 15488 outputs
DenseLayer (None, 500) produces 500 outputs
DenseLayer (None, 500) produces 500 outputs
DenseLayer (None, 30) produces 30 outputs

接下來我們看到，和第一個網(wǎng)絡(luò)輸出相同，是每一次迭代訓(xùn)練損失和驗證損失以及他們之間的比率。
Epoch | Train loss | Valid loss | Train / Val
--------|--------------|--------------|----------------
1 | 0.111763 | 0.042740 | 2.614934
2 | 0.018500 | 0.009413 | 1.965295
3 | 0.008598 | 0.007918 | 1.085823
4 | 0.007292 | 0.007284 | 1.001139
5 | 0.006783 | 0.006841 | 0.991525
...
500 | 0.001791 | 0.002013 | 0.889810
501 | 0.001789 | 0.002011 | 0.889433
502 | 0.001786 | 0.002009 | 0.889044
503 | 0.001783 | 0.002007 | 0.888534
504 | 0.001780 | 0.002004 | 0.888095
505 | 0.001777 | 0.002002 | 0.887699
...
995 | 0.001083 | 0.001568 | 0.690497
996 | 0.001082 | 0.001567 | 0.690216
997 | 0.001081 | 0.001567 | 0.689867
998 | 0.001080 | 0.001567 | 0.689595
999 | 0.001080 | 0.001567 | 0.689089
1000 | 0.001079 | 0.001566 | 0.688874

1000次迭代后的結(jié)果相對第一個網(wǎng)絡(luò)，有了非常不錯的改善，我們的RMSE也有不錯的結(jié)果。
>>> np.sqrt(0.001566) * 48
1.8994904579913006

我們從測試集合里面取同一個樣例，畫出兩個網(wǎng)絡(luò)的預(yù)測結(jié)果來進行對比：
sample1 = load(test=True)[0][6:7]
sample2 = load2d(test=True)[0][6:7]
y_pred1 = net1.predict(sample1)[0]
y_pred2 = net2.predict(sample2)[0]

fig = pyplot.figure(figsize=(6, 3))
ax = fig.add_subplot(1, 2, 1, xticks=[], yticks=[])
plot_sample(sample1[0], y_pred1, ax)
ax = fig.add_subplot(1, 2, 2, xticks=[], yticks=[])
plot_sample(sample1[0], y_pred2, ax)
pyplot.show()

左邊的net1的預(yù)測與net2的預(yù)測相比。

然后讓我們比較第一和第二網(wǎng)絡(luò)的學(xué)習(xí)曲線：

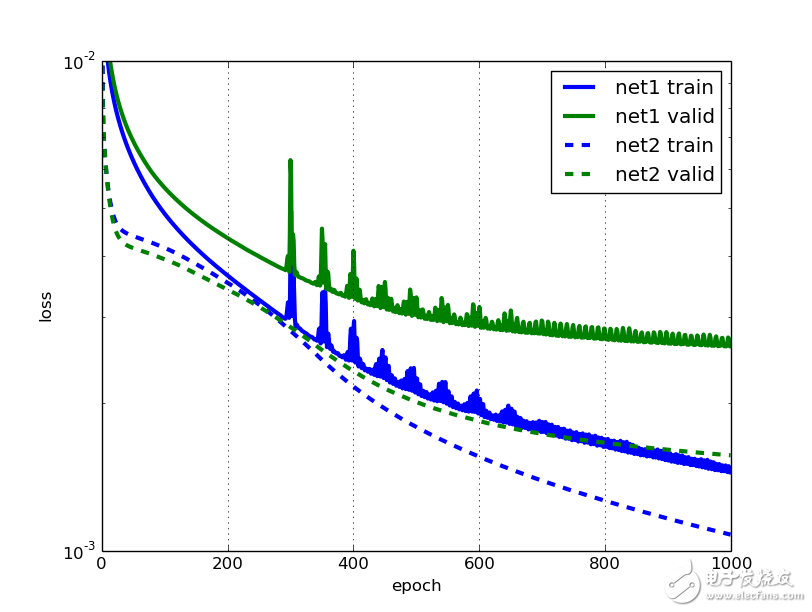
這看起來不錯，我喜歡新的誤差曲線的平滑度。 但是我們注意到，到最后，net2的驗證錯誤比訓(xùn)練錯誤更快地趨于水平。 我敢打賭，我們可以通過使用更多的培訓(xùn)示例來改善。 如果我們水平翻轉(zhuǎn)輸入圖像怎么辦？ 我們能夠通過使這樣的培訓(xùn)數(shù)據(jù)量增加一倍來改進培訓(xùn)嗎？

數(shù)據(jù)擴充

通常情況下，增加訓(xùn)練集的數(shù)量會讓一個過擬合的網(wǎng)絡(luò)取得更好的訓(xùn)練結(jié)果。（如果你的網(wǎng)絡(luò)沒有過擬合，那么你最好把它變大。（否則不足以描述數(shù)據(jù)））
數(shù)據(jù)擴充的意思是我們?nèi)藶榈赝ㄟ^一些手段（變形、添加噪聲等等）增加訓(xùn)練用例的個數(shù)。顯然，這要比手工收集更多的樣本經(jīng)濟許多。所以，數(shù)據(jù)擴充是深度學(xué)習(xí)工具箱里必不可少的工具。

我們曾經(jīng)在前面簡短的提到批處理迭代器。批量迭代器的工作是采集一個訓(xùn)練集合的樣本矩陣，分成不同的批次（在我們的任務(wù)128個用例一批）。當(dāng)把訓(xùn)練樣本分成批次的時候，批處理迭代器可以順便把輸入變形這件事做的又快又好。所以當(dāng)我們想要進行水平翻轉(zhuǎn)的時候，我們不需要去翻倍數(shù)量巨大的訓(xùn)練集合。更好的方法是，我們在進行批處理迭代的時候，以50%的幾率進行水平翻轉(zhuǎn)就可以了。這非常的方便，對某些問題來說這種手段可以讓我們生產(chǎn)近乎無限的訓(xùn)練集，而不需要增加內(nèi)存的使用。同時，輸入圖片的變形操作可以在GPU進行上一個批次運算的時候進行，所以可以說，這個操作幾乎不增加任何額外的資源消耗。

水平翻轉(zhuǎn)圖片事實上僅僅是矩陣的切片操作：
X, y = load2d()
X_flipped = X[:, :, :, ::-1] # simple slice to flip all images

# plot two images:
fig = pyplot.figure(figsize=(6, 3))
ax = fig.add_subplot(1, 2, 1, xticks=[], yticks=[])
plot_sample(X[1], y[1], ax)
ax = fig.add_subplot(1, 2, 2, xticks=[], yticks=[])
plot_sample(X_flipped[1], y[1], ax)
pyplot.show()

原始圖片（左）和翻轉(zhuǎn)圖片

在右邊的圖片中，值得注意的是關(guān)鍵點的位置并不匹配。因為我們翻轉(zhuǎn)了圖片，所以我們也必須翻轉(zhuǎn)目標(biāo)位置的橫坐標(biāo)，同時，還要交換目標(biāo)值的位置，因為left_eye_center_x 變換過之后的值，指示的實際上是right_eye_center_x。我們建立一個元組flip_indices來保存哪一列的目標(biāo)向量需要交換位置。如果你還記得，最開始的時候我們讀取的數(shù)據(jù)條數(shù)是這樣的：
left_eye_center_x 7034
left_eye_center_y 7034
right_eye_center_x 7032
right_eye_center_y 7032
left_eye_inner_corner_x 2266
left_eye_inner_corner_y 2266
…

因為left_eye_center_x要和right_eye_center_x換位置，我們記錄（0,2），同樣left_eye_center_y要和right_eye_center_y換位置，我們記錄元組(1,3)，以此類推。最后，我們獲得元組集合如下：
flip_indices = [
(0, 2), (1, 3),
(4, 8), (5, 9), (6, 10), (7, 11),
(12, 16), (13, 17), (14, 18), (15, 19),
(22, 24), (23, 25),
]

# Let's see if we got it right:
df = read_csv(os.path.expanduser(FTRAIN))
for i, j in flip_indices:
print("# {} -> {}".format(df.columns[i], df.columns[j]))

# this prints out:
# left_eye_center_x -> right_eye_center_x
# left_eye_center_y -> right_eye_center_y
# left_eye_inner_corner_x -> right_eye_inner_corner_x
# left_eye_inner_corner_y -> right_eye_inner_corner_y
# left_eye_outer_corner_x -> right_eye_outer_corner_x
# left_eye_outer_corner_y -> right_eye_outer_corner_y
# left_eyebrow_inner_end_x -> right_eyebrow_inner_end_x
# left_eyebrow_inner_end_y -> right_eyebrow_inner_end_y
# left_eyebrow_outer_end_x -> right_eyebrow_outer_end_x
# left_eyebrow_outer_end_y -> right_eyebrow_outer_end_y
# mouth_left_corner_x -> mouth_right_corner_x
# mouth_left_corner_y -> mouth_right_corner_y

我們的批處理迭代器的實現(xiàn)將會從BachIterator類派生，重載transform()方法。把這些東西組合到一起，看看完整的代碼：
from nolearn.lasagne import BatchIterator

class FlipBatchIterator(BatchIterator):
flip_indices = [
(0, 2), (1, 3),
(4, 8), (5, 9), (6, 10), (7, 11),
(12, 16), (13, 17), (14, 18), (15, 19),
(22, 24), (23, 25),
]

def transform(self, Xb, yb):
Xb, yb = super(FlipBatchIterator, self).transform(Xb, yb)

# Flip half of the images in this batch at random:
bs = Xb.shape[0]
indices = np.random.choice(bs, bs / 2, replace=False)
Xb[indices] = Xb[indices, :, :, ::-1]

if yb is not None:
# Horizontal flip of all x coordinates:
yb[indices, ::2] = yb[indices, ::2] * -1

# Swap places, e.g. left_eye_center_x -> right_eye_center_x
for a, b in self.flip_indices:
yb[indices, a], yb[indices, b] = (
yb[indices, b], yb[indices, a])

return Xb, yb

使用上述批處理迭代器進行訓(xùn)練，需要把它作為batch_iterator_train參數(shù)傳遞給NeuralNet。讓我們來定義net3，一個和net2非常相似的網(wǎng)絡(luò)。僅僅是在網(wǎng)絡(luò)的最后添加了這些行：
net3 = NeuralNet(
# ...
regression=True,
batch_iterator_train=FlipBatchIterator(batch_size=128),
max_epochs=3000,
verbose=1,
)

現(xiàn)在我們已經(jīng)采用了最新的翻轉(zhuǎn)技巧，但同時我們將迭代次數(shù)增長了三倍。因為我們并沒有真正改變訓(xùn)練集合的總數(shù)，所以每個epoch仍然使用和剛剛一樣多的樣本個數(shù)。事實證明，采用了新技巧后，每個訓(xùn)練epoch還是比剛剛多用了一些時間。這次我們的網(wǎng)絡(luò)學(xué)到的東西更具一般性，理論上來講學(xué)習(xí)更一般性的規(guī)律比學(xué)出過擬合總是要更難一些。

這次網(wǎng)絡(luò)將花費一小時的訓(xùn)練時間，我們要確保在訓(xùn)練之后，把得到的模型保存起來。然后就可以去喝杯茶或者做做家務(wù)活，洗衣服也是不錯的選擇。
net3.fit(X, y)

import cPickle as pickle
with open('net3.pickle', 'wb') as f:
pickle.dump(net3, f, -1)
1
2
3
4
5

1
2
3
4
5
$ python kfkd.py
...
Epoch | Train loss | Valid loss | Train / Val
--------|--------------|--------------|----------------
...
500 | 0.002238 | 0.002303 | 0.971519
...
1000 | 0.001365 | 0.001623 | 0.841110
1500 | 0.001067 | 0.001457 | 0.732018
2000 | 0.000895 | 0.001369 | 0.653721
2500 | 0.000761 | 0.001320 | 0.576831
3000 | 0.000678 | 0.001288 | 0.526410

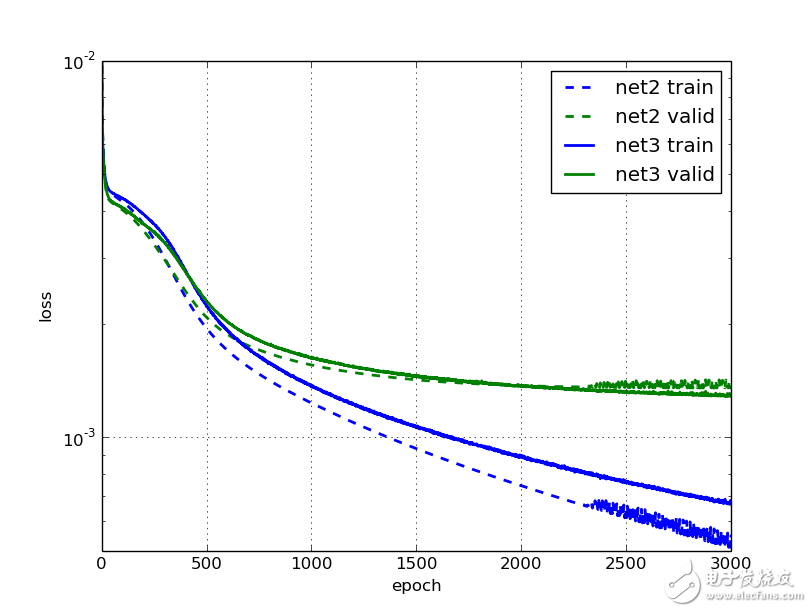
讓我們畫出學(xué)習(xí)曲線和net2對比。應(yīng)該看到3000次迭代后的效果，net3比net2的驗證損失要小了5%。我們看到在2000次迭代之后，net2已經(jīng)停止學(xué)習(xí)了，并且曲線變得不光滑；但是net3的效果卻在一直改進，盡管進展緩慢。