傅里葉變換是一種在各種科學和工程領域中發揮了關鍵作用的數學技術,其應用范圍從信號處理到量子力學。近年來,它在機器學習領域找到了新的重要性。本文探討了傅里葉變換的基本原理及其在機器學習應用中日益增長的重要性。
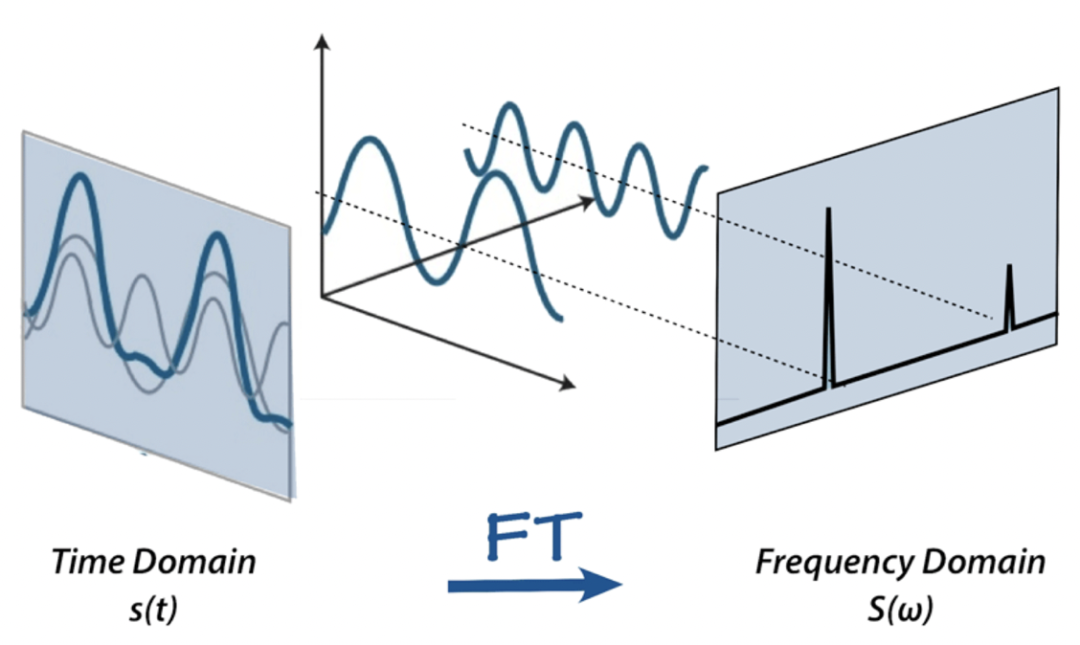
傅里葉變換通過頻域分析,讓我們看到了另一份觀景,在機器學習領域也同樣適用。
理解傅立葉變換
傅里葉變換以法國數學家和物理學家讓-巴蒂斯特·約瑟夫·傅里葉命名,它是一種數學運算,將信號分解為其組成的頻率成分。它允許我們分析信號的頻率內容,并在頻域中表示它。這種轉換在處理復雜信號時特別有用,因為它簡化了對其潛在模式的分析。

img
連續傅里葉變換(CFT)和離散傅里葉變換(DFT)是兩個常見的變體。CFT用于連續信號,而DFT應用于離散信號,使其與數字數據和機器學習任務更加相關。快速傅里葉變換(FFT)是計算DFT的有效算法,進一步促進了其在各種應用中的廣泛使用。
FFT在信號處理的應用
傅里葉變換最傳統且確立的應用之一是在信號處理中。它被用于音頻處理、圖像分析和數據壓縮等任務。例如,在音頻處理中,傅里葉變換幫助識別音頻信號中存在各種頻率,使得可以進行語音識別、音樂分類和降噪等任務。
在圖像分析中,傅里葉變換可用于從圖像中提取紋理和圖案信息。通過將圖像轉換到頻域,更容易檢測邊緣、形狀和其他視覺特征。這對于圖像識別、物體檢測和圖像壓縮等任務至關重要。
FFT在機器學習的應用
機器學習是一個專注于開發能夠從數據中學習算法的領域,已經看到傅里葉變換的使用日益增多。它在這個領域的應用多樣且有影響力:
時間序列分析:在金融、醫療保健和天氣預報等領域,時間序列數據豐富。傅里葉變換可以通過分析其頻率成分來幫助提取時間序列數據的相關特征。這對于異常檢測、趨勢分析和預測等任務至關重要。
自然語言處理:當文本數據被表示為單詞序列時,可以被視為離散信號。通過應用傅里葉變換,可以在頻域中分析文本數據,這在文本分類、情感分析和主題建模中有應用。
特征工程:特征工程是機器學習流程中的一個關鍵步驟。通過將數據轉換到頻域,可以提取可能在時域中難以捕捉的寶貴特征。這可能導致更強大和準確的機器學習模型。
卷積神經網絡(CNN):CNN是一種用于圖像分析的流行深度學習架構。傅里葉變換可用于設計專門檢測圖像中某些頻率成分的卷積濾波器。這可以提高CNN在圖像分類和物體識別等任務中的性能。
數據增強:數據增強是一種用于增加訓練數據集大小的技術。在圖像處理中,可以通過改變圖像的頻率成分來使用傅里葉變換創建增強數據。這有助于提高機器學習模型的泛化能力和魯棒性。
代碼
要在Python中進行時間序列分析的傅里葉變換,您可以使用numpy和matplotlib庫。我將為您提供一個完整的Python代碼示例,該示例使用一個樣本數據集并生成相關圖表。首先,如果您還沒有安裝必要的庫,您需要安裝它們:
pip?install?numpy?matplotlib
以下是使用傅里葉變換進行時間序列分析的Python代碼,包含了一個樣本數據集和圖表:
import?numpy?as?np import?matplotlib.pyplot?as?plt #?Generate?a?sample?time?series?dataset #?You?can?replace?this?with?your?own?time?series?data #?Ensure?that?the?data?is?in?a?NumPy?array?or?a?list time?=?np.arange(0,?10,?0.01)??#?Time?values?from?0?to?10?with?a?step?of?0.01 signal?=?2?*?np.sin(2?*?np.pi?*?1?*?time)?+?1?*?np.sin(2?*?np.pi?*?2?*?time) #?Plot?the?original?time?series plt.figure(figsize=(10,?4)) plt.subplot(2,?1,?1) plt.plot(time,?signal) plt.title('Original?Time?Series') plt.xlabel('Time') plt.ylabel('Amplitude') #?Perform?the?Fourier?Transform fourier_transform?=?np.fft.fft(signal) frequencies?=?np.fft.fftfreq(len(signal),?0.01)??#?Frequency?values?(assuming?a?sampling?interval?of?0.01) #?Plot?the?magnitude?of?the?Fourier?Transform plt.subplot(2,?1,?2) plt.plot(frequencies,?np.abs(fourier_transform)) plt.title('Fourier?Transform') plt.xlabel('Frequency?(Hz)') plt.ylabel('Magnitude') plt.xlim(0,?5)??#?Limit?the?x-axis?to?show?frequencies?up?to?5?Hz plt.tight_layout() plt.show()
上述代碼中:
我們生成一個包含兩個正弦成分的樣本時間序列數據集。您應該用您自己的時間序列數據替換這個。
我們使用np.fft.fft對時間序列數據執行傅里葉變換。
我們使用np.fft.fftfreq計算對應的頻率。
我們創建兩個子圖:一個用于原始時間序列,另一個用于傅里葉變換的幅度。
最后,我們使用plt.show()顯示圖表。
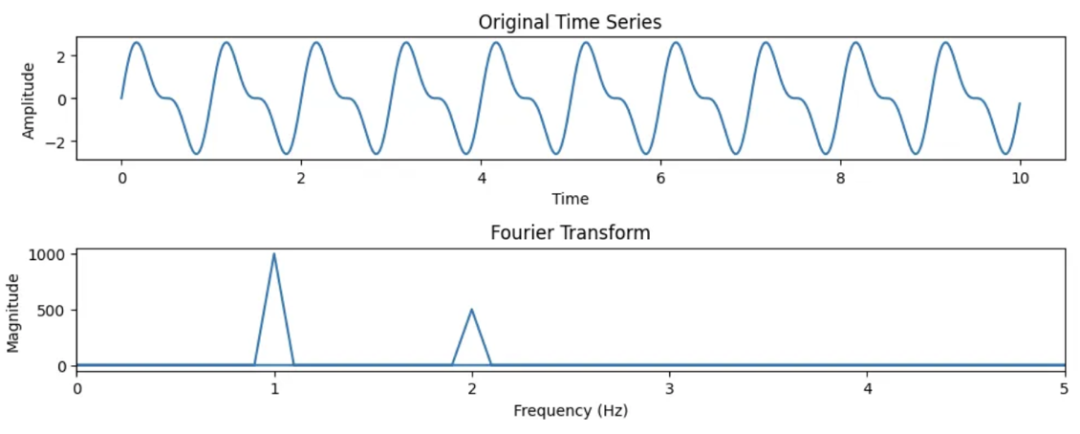
確保在處理實際數據時,將樣本數據集替換為您自己的時間序列數據。上述代碼將為您提供原始時間序列和傅里葉變換幅度的圖表。您可以根據特定需求調整繪圖參數和標簽。
結論
傅里葉變換最初是為信號處理而開發的,現在已經深入到機器學習的核心。它在各種ML應用中分析和提取頻率信息的能力是無價的,包括時間序列分析、自然語言處理、特征工程以及增強深度學習模型。隨著機器學習繼續發展和擴展其視野,傅里葉變換仍然是一個強大的工具,使研究人員和從業者能夠解鎖更深層次的洞察力并開發更有效的算法。它的多功能性和適應性使其成為現代機器學習工具箱中不可或缺的組成部分。
審核編輯:黃飛
?
 電子發燒友App
電子發燒友App
























評論