四、卷積神經網絡LeNet-5結構分析

?

?

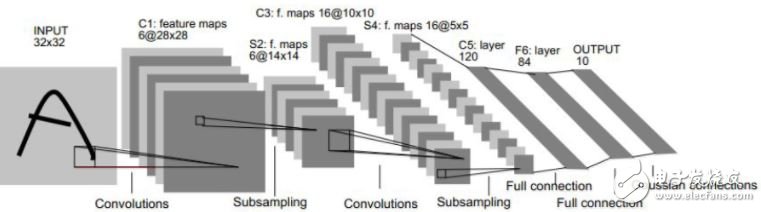
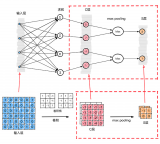
CNN是一種帶有卷積結構的深度神經網絡，通常至少有兩個非線性可訓練的卷積層，兩個非線性的固定卷積層（又叫Pooling Layer或降采樣層）和一個全連接層，一共至少5個隱含層。

CNN的結構受到著名的Hubel-Wiesel生物視覺模型的啟發，尤其是模擬視覺皮層V1和V2層中Simple Cell和Complex Cell的行為。

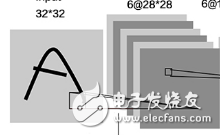
LeNet-5手寫數字識別結構(上圖)分析：

1. 輸入層：N個32*32的訓練樣本
輸入圖像為32*32大小。這要比Mnist數據庫中最大的字母還大。這樣做的原因是希望潛在的明顯特征如筆畫斷點或角點能夠出現在最高層特征監測子感受野的中心。

2. C1層：
輸入圖片大小： 32*32
卷積窗大小： 5*5
卷積窗種類： 6
輸出特征圖數量： 6
輸出特征圖大小： 28*28 (32-5+1)
神經元數量： 4707 (28*28)*6)
連接數： 122304 (28*28*5*5*6)+(28*28*6)
可訓練參數： 156 5*5*6+6

用6個5×5的過濾器進行卷積，結果是在卷積層C1中，得到6張特征圖，特征圖的每個神經元與輸入圖片中的5×5的鄰域相連，即用5×5的卷積核去卷積輸入層，由卷積運算可得C1層輸出的特征圖大小為(32-5+1)×(32-5+1)=28×28。

3. S2層：
輸入圖片大小： (28*28)*6
卷積窗大小： 2*2
卷積窗種類： 6
輸出下采樣圖數量：6
輸出下采樣圖大小：14*14 (28/2)*(28/2)
神經元數量： 1176 (14*14)*6
連接數： 5880 2*2*14*14*6+14*14*6
可訓練參數： 12 1*6+6

卷積和子采樣過程：

(1)、卷積過程包括：用一個可訓練的濾波器fx去卷積一個輸入的圖像（第一階段是輸入的圖像，后面的階段就是卷積特征map了），然后加一個偏置bx，得到卷積層Cx。

卷積運算一個重要的特點就是，通過卷積運算，可以使原信號特征增強，并且降低噪音。

(2)、子采樣過程包括：每鄰域四個像素求和變為一個像素，然后通過標量Wx+1加權，再增加偏置bx+1，然后通過一個sigmoid激活函數，產生一個大概縮小四倍的特征映射圖Sx+1。

利用圖像局部相關性的原理，對圖像進行子抽樣，可以減少數據處理量同時保留有用信息。

卷積之后進行子抽樣的思想是受到動物視覺系統中的“簡單的”細胞后面跟著“復雜的”細胞的想法的啟發而產生的。

降采樣后，降采樣層S2的輸出特征圖大小為（28÷2）×（28÷2）=14×14。

S2層每個單元的4個輸入相加，乘以一個可訓練參數，再加上一個可訓練偏置。結果通過sigmoid函數計算。可訓練系數和偏置控制著sigmoid函數的非線性程度。如果系數比較小，那么運算近似于線性運算，下采樣相當于模糊圖像。如果系數比較大，根據偏置的大小下采樣可以被看成是有噪聲的“或”運算或者有噪聲的“與”運算。每個單元的2*2感受野并不重疊，因此S2中每個特征圖的大小是C1中特征圖大小的1/4（行和列各1/2）。

從一個平面到下一個平面的映射可以看作是作卷積運算，S-層可看作是模糊濾波器，起到二次特征提取的作用。隱層與隱層之間空間分辨率遞減，而每層所含的平面數遞增，這樣可用于檢測更多的特征信息。

4. C3層：
輸入圖片大小： (14*14)*6
卷積窗大小： 5*5
卷積窗種類： 16
輸出特征圖數量： 16
輸出特征圖大小： 10*10 (14-5+1)
神經元數量： 1600 (10*10)*16)
連接數： 151600 1516*10*10
可訓練參數： 1516 6*(3*25+1)+6*(4*25+1)+3*(4*25+1)+1*(6*25+1)

C3層也是一個卷積層，它同樣通過5x5的卷積核去卷積S2層，然后得到的特征map就只有10x10個神經元，但是它有16種不同的卷積核，所以就存在16個特征map了。這里需要注意的一點是：C3中的每個特征map是連接到S2中的所有6個或者幾個特征map的，表示本層的特征map是上一層提取到的特征map的不同組合（這個做法也并不是唯一的）。

C3中每個特征圖由S2中所有6個或者幾個特征map組合而成。為什么不把S2中的每個特征圖連接到每個C3的特征圖呢？原因有2點。第一，不完全的連接機制將連接的數量保持在合理的范圍內。第二，也是最重要的，其破壞了網絡的對稱性。由于不同的特征圖有不同的輸入，所以迫使他們抽取不同的特征。

5. S4層：
輸入圖片大小： (10*10)*16
卷積窗大小： 2*2
卷積窗種類： 16
輸出下采樣圖數量： 16
輸出下采樣圖大小： (5*5)*16
神經元數量： 400 (5*5)*16
連接數： 2000 (2*2*5*5*16)+(5*5*16)
可訓練參數： 32 (1+1)*16

S4層是一個下采樣層，由16個5*5大小的特征圖構成。特征圖中的每個單元與C3中相應特征圖的2*2鄰域相連接，跟C1和S2之間的連接一樣。S4層有32個可訓練參數（每個特征圖1個因子和一個偏置）和2000個連接。

6. C5層：
輸入圖片大小： (5*5)*16
卷積窗大小： 5*5
卷積窗種類： 120
輸出特征圖數量： 120
輸出特征圖大小： 1*1 (5-5+1)
神經元數量： 120 (1*120)
連接數： 48120 5*5*16*120*1+120*1
可訓練參數： 48120 5*5*16*120+120

C5層是一個卷積層，有120個特征圖。每個單元與S4層的全部16個單元的5*5鄰域相連。由于S4層特征圖的大小也為5*5（同濾波器一樣），故C5特征圖的大小為1*1，這構成了S4和C5之間的全連接。之所以仍將C5標示為卷積層而非全相聯層，是因為如果LeNet-5的輸入變大，而其他的保持不變，那么此時特征圖的維數就會比1*1大。C5層有48120個可訓練連接。

7. F6層：
輸入圖片大小： (1*1)*120
卷積窗大小： 1*1
卷積窗種類： 84
輸出特征圖數量： 1
輸出特征圖大小： 84
神經元數量： 84
連接數： 10164 120*84+84
可訓練參數： 10164 120*84+84

F6層有84個單元（之所以選這個數字的原因來自于輸出層的設計），與C5層全相連。有10164個可訓練參數。如同經典神經網絡，F6層計算輸入向量和權重向量之間的點積，再加上一個偏置。然后將其傳遞給sigmoid函數產生單元i的一個狀態。

8. OUTPUT層：
輸入圖片大小： 1*84
輸出特征圖數量： 1*10

最后，輸出層由歐式徑向基函數（EuclideanRadial Basis Function）單元組成，每類一個單元，每個有84個輸入。換句話說，每個輸出RBF單元計算輸入向量和參數向量之間的歐式距離。輸入離參數向量越遠，RBF輸出的越大。一個RBF輸出可以被理解為衡量輸入模式和與RBF相關聯類的一個模型的匹配程度的懲罰項。用概率術語來說，RBF輸出可以被理解為F6層配置空間的高斯分布的負log-likelihood。給定一個輸入模式，損失函數應能使得F6的配置與RBF參數向量（即模式的期望分類）足夠接近。這些單元的參數是人工選取并保持固定的（至少初始時候如此）。這些參數向量的成分被設為-1或1。雖然這些參數可以以-1和1等概率的方式任選，或者構成一個糾錯碼，但是被設計成一個相應字符類的7*12大小（即84）的格式化圖片。這種表示對識別單獨的數字不是很有用，但是對識別可打印ASCII集中的字符串很有用。

使用這種分布編碼而非更常用的“1 of N”編碼用于產生輸出的另一個原因是，當類別比較大的時候，非分布編碼的效果比較差。原因是大多數時間非分布編碼的輸出必須為0。這使得用sigmoid單元很難實現。另一個原因是分類器不僅用于識別字母，也用于拒絕非字母。使用分布編碼的RBF更適合該目標。因為與sigmoid不同，他們在輸入空間的較好限制的區域內興奮，而非典型模式更容易落到外邊。

RBF參數向量起著F6層目標向量的角色。需要指出這些向量的成分是+1或-1，這正好在F6 sigmoid的范圍內，因此可以防止sigmoid函數飽和。實際上，+1和-1是sigmoid函數的最大彎曲的點處。這使得F6單元運行在最大非線性范圍內。必須避免sigmoid函數的飽和，因為這將會導致損失函數較慢的收斂和病態問題。