所謂傳遞函數即線性定常系統在零初始條件下,輸出量的拉氏變換式與輸入量的拉氏變換式之比。傳遞函數通常用于單輸入、單輸出的模擬電路,主要用在信號處理、通信理論、控制理論。這個術語經常專門用于如本文所述的線性時不變系統(LTI)。實際系統基本都有非線性的輸入輸出特性,但是許多系統在標稱參數范圍內的運行狀態非常接近于線性,所以實際應用中完全可以應用線性時不變系統理論表示其輸入輸出行為,有的書中也把其譯為:“轉移函數”。
n階濾波器傳遞函數的一般表達式為
![]()
若將傳遞函數分解為因子式,則上式變為
![]()
式中,sao?,sa1,…,sas咖為傳遞函數的極點;sbo,sb1執,…,sbm為傳遞函數的零點。
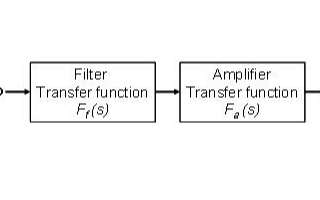
在設計濾波器的電路時,直接實現3階以上傳遞函數的電路是很難的。當需要設計大于或即是3階的濾波器時,一般采取將高階傳遞函數分解為幾個低階傳遞函數乘積的形式。如
Gn(s)=G1(S).G2(S)… Gk(s)
式中,k≤n。例如,設計一個5階濾波器,可用兩個2階濾波器和一個1階濾波器級聯得到。
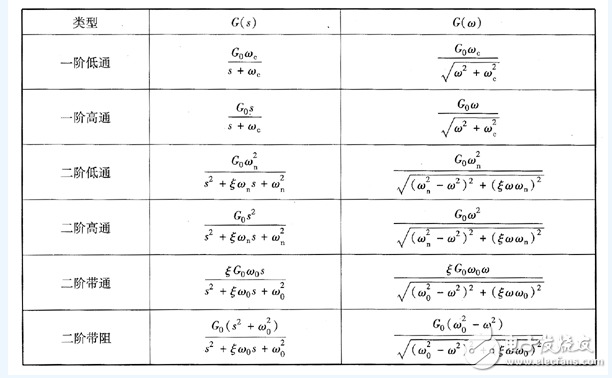
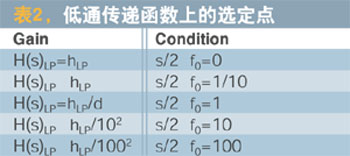
表中,G(s)為濾波器的傳遞函數,c(ω)為濾波器的幅頻特性,G0為濾波器的通帶增益或零頻增益,ωc為一階濾波器的截止角頻率,ωn為二階濾波器的自然角頻率,ω0為帶通或帶阻濾波器的中心頻率,ε為2階濾波器的阻尼系數。
將k個低階傳遞函數的濾波器的基本節級聯起來,可構成n階濾波器。由于用集成運放構成的低階濾波器,其輸出阻抗很低9所以不必考慮各基本節級聯時的負載效應,保證了各基本節傳遞函數設計的獨立性。
一階濾波器和二階濾波器是設計集成有源濾波器的基礎,表列出了常用的一階、二階濾波器的傳遞函數和幅頻特性。在設計濾波器時,可直接查表得到其傳遞函數,這樣就避免了在設計濾波器時求解傳遞函數的麻煩。
二階低通濾波器
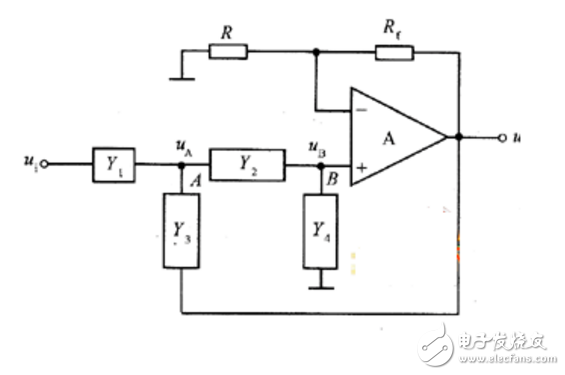
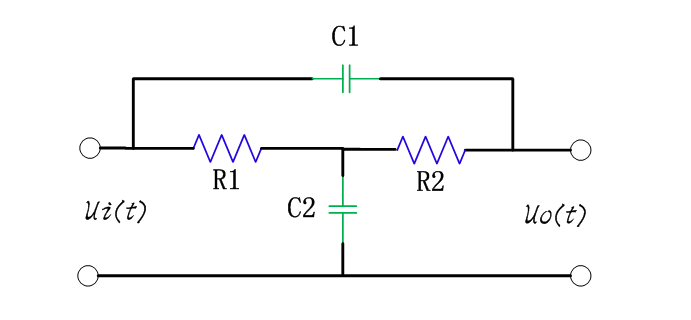
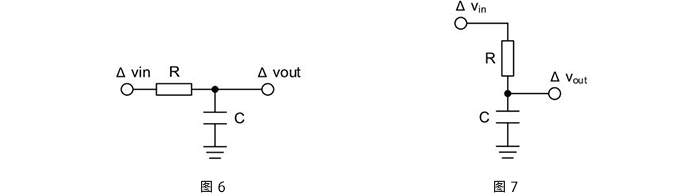
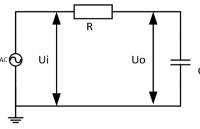
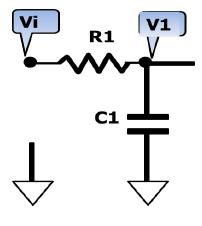
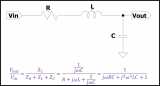
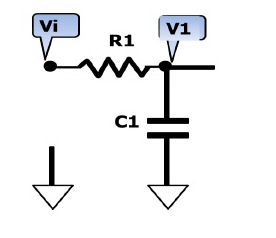
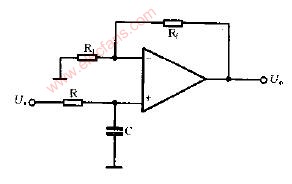
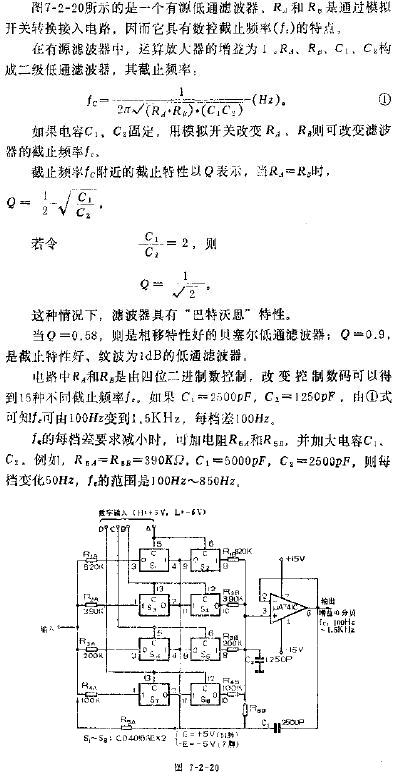
為了改進一階低通濾波器的頻率特性,可采用二階低通濾波器。一個二階低通濾波器包含兩個RC支路,如圖所示為二階低通濾波器的一般電路。此一般電路對于二階高通濾波器也同樣適用。 圖6-2-3所示的濾波器是同相放大器。在圖6-2-3中,零頻增益為
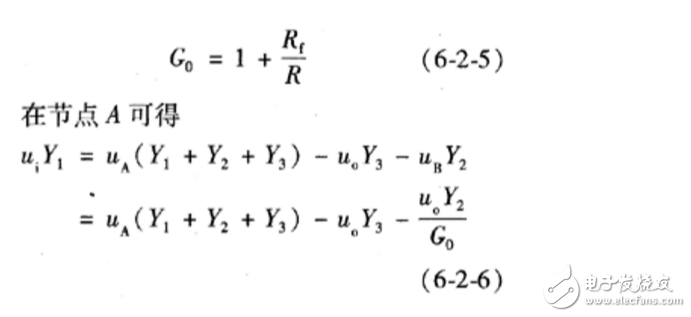
在節點B可得
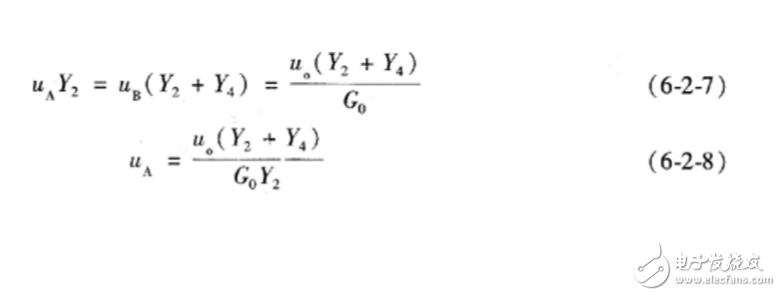
將式(6-2-8)代人式(6-2-6),轉變到復頻域,可得一般二階低通濾波器的傳遞函數為
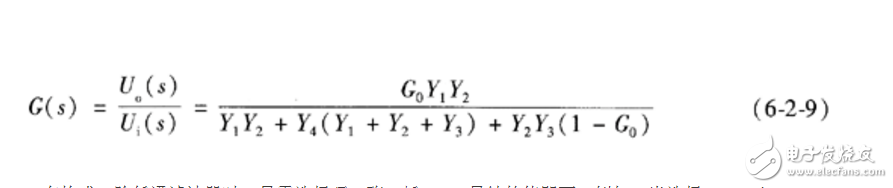
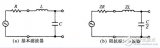
在構成二階低通濾波器時,只需選擇巧,殤,蠔,‰導納的值即可。例如,當選擇Y1=1/R1,Y2=1/R2,Y3=sC1 Y4=sC2時,則構成圖6-2-4所示的二階低通濾波器。
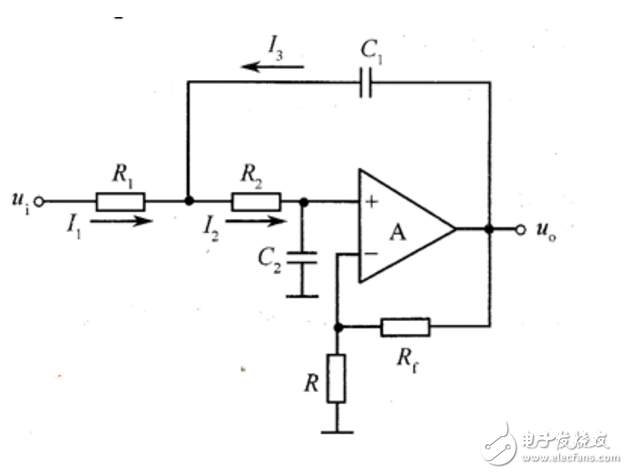
對于上圖所示的二階低通濾波器,其傳遞函數為

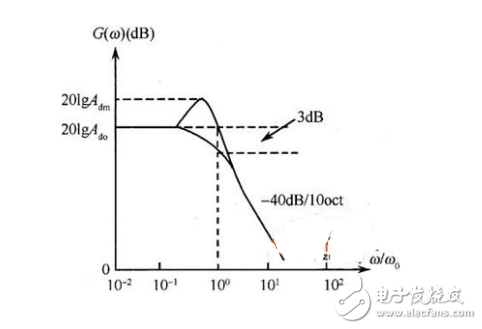
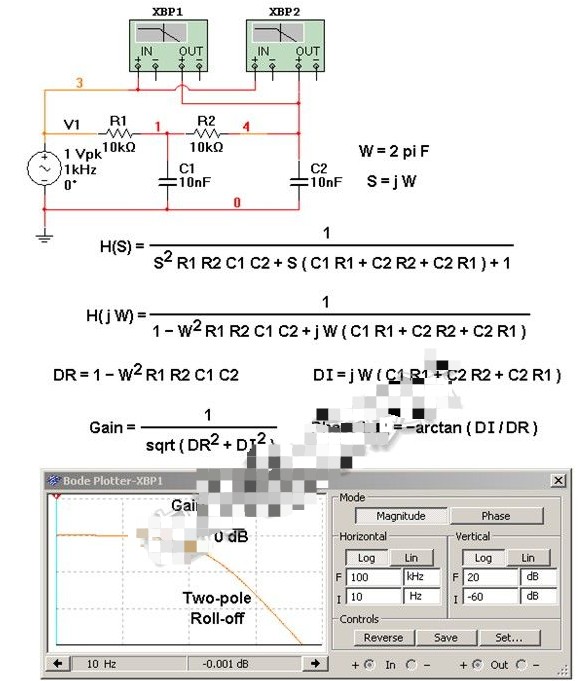
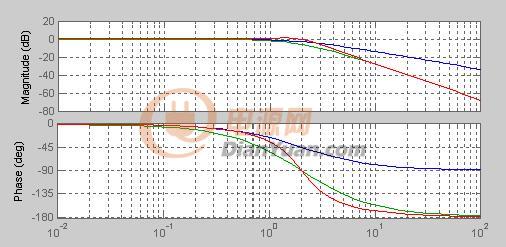
如圖6-2-5所示為二階低通濾波器的幅頻特性曲線,其阻帶衰減特性的斜率為-40dB/10oct,克服了一階低通濾波器阻帶衰減太慢的缺點。
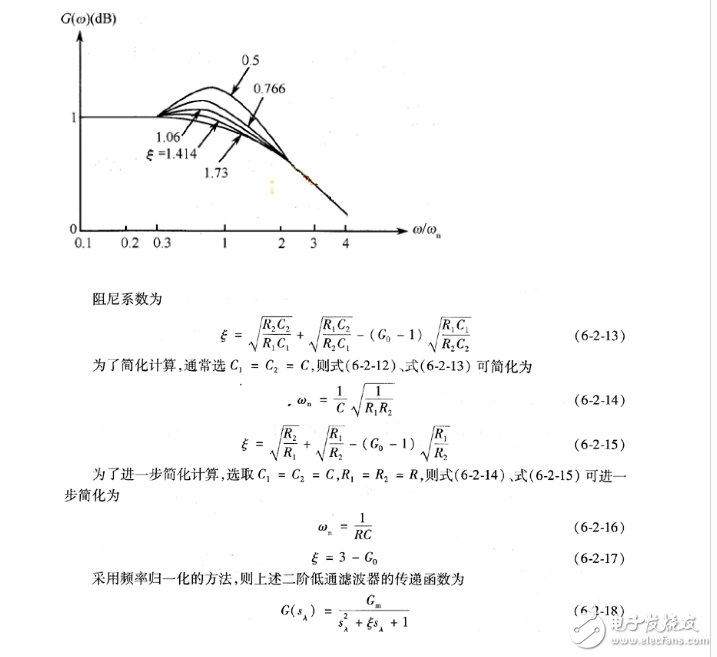
二階低通濾波器的各個參數,影響其濾波特性,如阻尼系數苫的大小,決定了幅頻特性有無峰值,或諧振峰的高低。如圖6=2-6所示為苫對二階低通濾波器幅頻特性的影響。
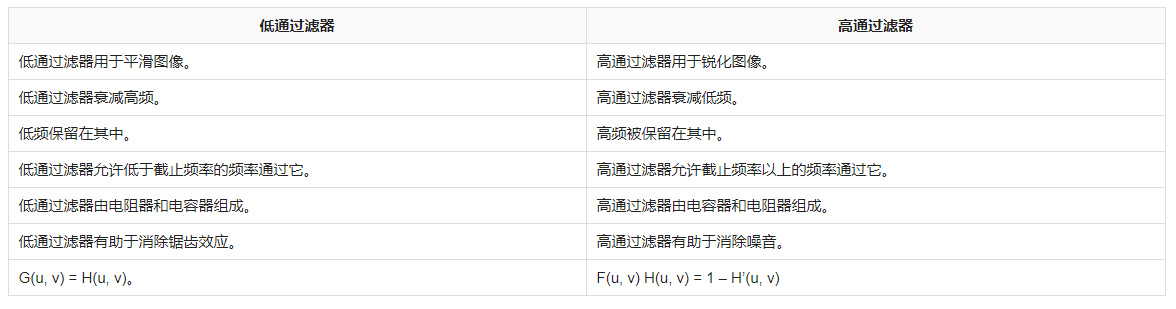
由傳遞函數判斷濾波器
根據系統函數快速判斷濾波器類型
(1)死辦法,用傅里葉變換求出H(f),在畫出幅頻特性曲線,看高頻部分是不是“通”
(2)用拉氏變換求出H(s),然后記住一句話:分子上有什么就通什么!
舉個例子:
H(s)=as/(bs+c)
分子上有“高次”,所以是高通。
這里的“高次”是這個意思:
分母上有s的0次和1次,分子是s的1次,所以是較高的那個,簡稱“高次”。
H(s)=a/(bs+c)
分子上有“低次”,所以是低通。
H(s)=as^2/(bs^2+cs+d)
分子上有“高次”,所以是高通。
H(s)=a/(bs^2+cs+d)
分子上有“低次”,所以是低通。
H(s)=as/(bs^2+cs+d)
分子上有“中間次”,所以是帶通。
第(2)種方法還沒找到理論根據,如果將分子分母都除以“高次”,在判斷頻率從小變化到無窮的情況能理解
如果只有一個零極點,可以根據復平面上零極點位置來判斷。
 電子發燒友App
電子發燒友App








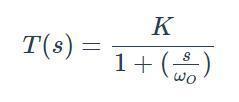
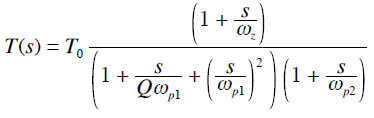
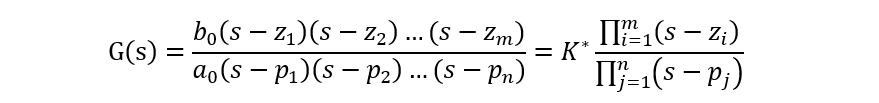
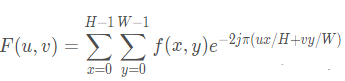




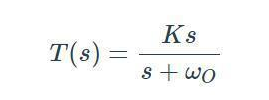


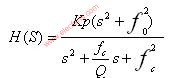










評論