傳遞函數表示線性定常系統自身,將輸入信號變換成輸出信號的能力。這是線性定常系統自身的特點,一個不同的輸入就會有一個不同的輸出。輸入信號本身不影響傳遞函數,傳遞函數是我這個系統自身決定的。
獲得傳遞函數的方法多種多樣,可以直接使用微分方程進行變換,也可以使用復阻抗法求取。但重要的是變換傳遞函數的能力,針對不同應用場合,變換傳遞函數的形式。閱讀傳遞函數的能力,比如通過傳遞函數能否看出系統極點和零點的位置,以及增益。
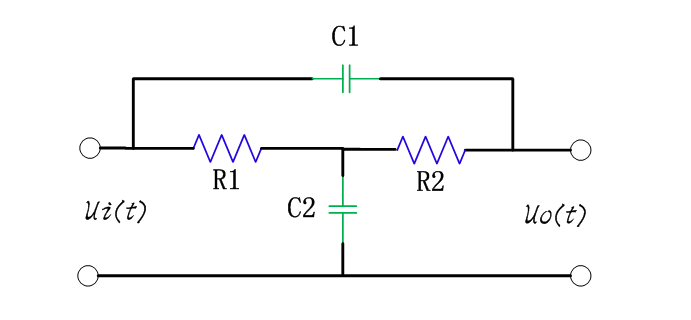
根據線性網絡理論,由電容、電阻和電感組成的電路網絡,其傳遞函數H可以用如下通用式表示:
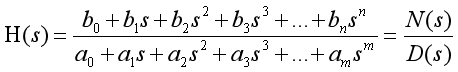
在這個式子中,很重要的一點是分母的階數m必須大于或等于分子的階數n。當m>n時,H(s)的幅值會隨著s趨于無窮而趨于0,滿足該性質的傳遞函數為”嚴格正則”。分母多項式D(s)階數反映了該電路網絡的階數。讓分母多項式D(s)=0,解出的所有根稱為系統的極點,讓分子多項式N(s)等于0,解出的所有根為系統的零點。
傳遞函數是一個分式,分子和分母都是多項式。基于應用場合的不同,它有三種常見的變換形式:
第1種傳遞函數寫法:在因式分解的時候,使s的最高項系數為1時。這種形式一眼就可以看出它的零點和極點。這個形式是傳遞函數根軌跡形式,也稱為首1型傳遞函數形式。這個時候提出來的常數,叫作根軌跡增益。應用在根軌跡的場合。
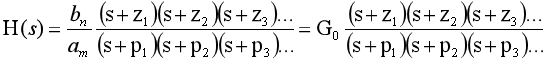
第2種傳遞函數寫法:在作因式分解的時候,常數項全部提出來,常數項變為1,通俗的說我們叫尾1型傳遞函數形式。這個時候提出來的系數我們叫作環路增益或者叫開環增益。應用在bode圖繪制,奈氏圖繪制,系統開環頻率響應分析的場合。
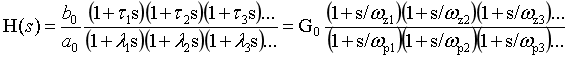
這兩個系數有什么關系,b0和bm有什么關系,b0=bm*z1*....zm。從數學角度看,就是提取公因式的事情,提的大和提的小的問題。提的小是前面的系數,提的大是后面的系數。
第3種傳遞函數寫法:當傳遞函數帶有積分環節,可以寫成這種形式。這種形式應用在環路補償的場合。
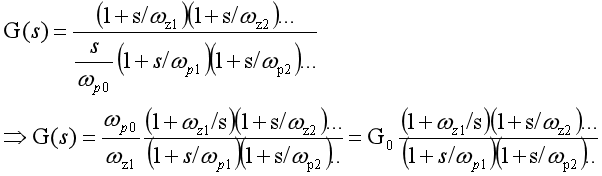
wp0是什么呢?
引入一個概念,稱為“0dB穿越極點”。對于包含原點極點的傳遞函數,也就是當s=0時,傳遞函數的幅值趨于無窮大。通常原點極點的s會帶有一個系數,例如1/[sRC(1+...)],可以將其重寫為如下形式:
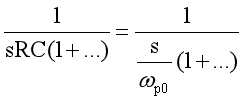
式中,wp0就是“0dB穿越極點”,它在上式中等于1/RC,對應截止頻率,也就是說s=wp0時,wp0/s的幅值等于1(或0dB)。
下圖種畫出了wp0/s的幅值與頻率的關系,是一條斜率為負的斜線。
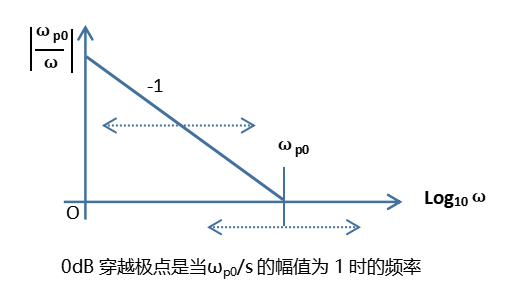
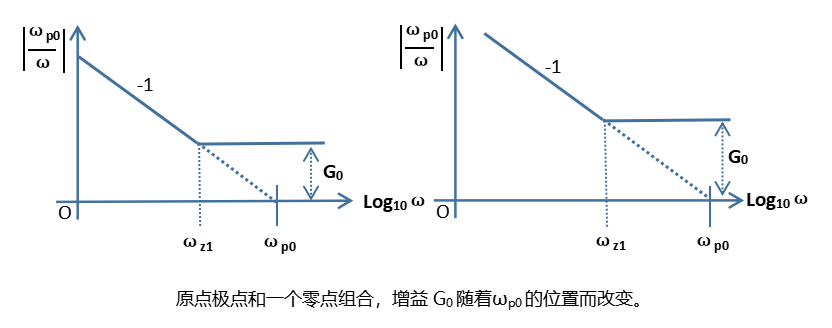
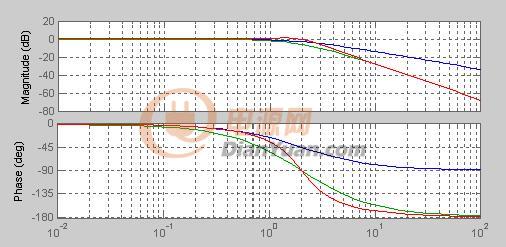
當原點極點與一個零點組合在一起時,斜線會在零點頻率處轉折并維持在增益G0,G0稱為中頻增益。下圖顯示了不同wp0的幅值-頻率關系。
審核編輯:湯梓紅
-
傳遞函數
+關注
關注
0文章
103瀏覽量
14217
原文標題:傳遞函數的三種形式及應用場合
文章出處:【微信號:yingjiansanrenxing,微信公眾號:硬件三人行】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
放大器的傳遞函數-誤差放大器、電壓放大器、電流放大器的傳遞函數導出
開環傳遞函數是怎樣影響系統的?
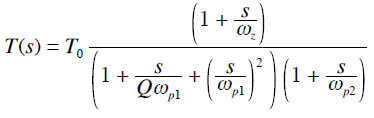
斜率的傳遞函數:電壓模式的傳遞函數
基于Butterworth標準傳遞函數設計
傳遞函數極點和零點的影響是什么
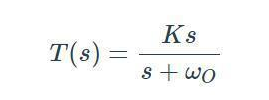
傳遞函數的頻率特性





 傳遞函數的三種形式及應用場合
傳遞函數的三種形式及應用場合
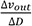










評論