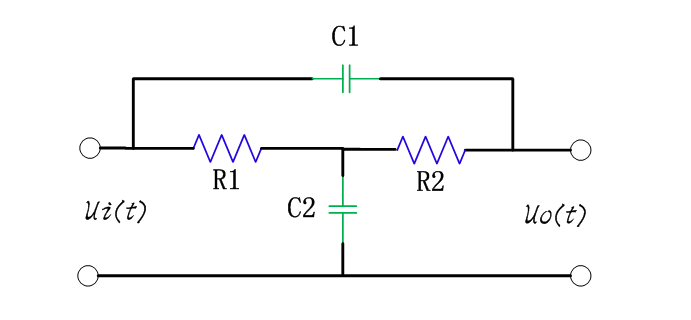
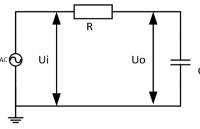
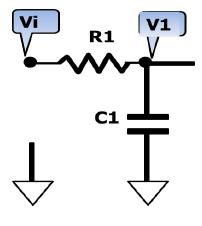
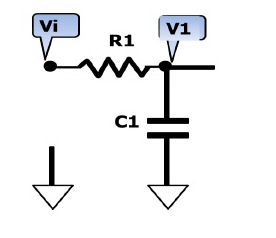
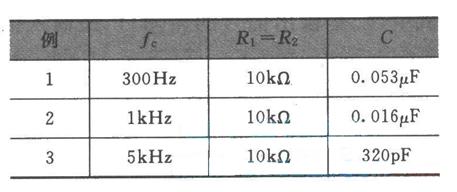
在構(gòu)成二階低通濾波器時(shí),只需選擇巧,殤,蠔,‰導(dǎo)納的值即可。例如,當(dāng)選擇Y1=1/R1,Y2=1/R2,Y3=sC1 Y4=sC2時(shí),則構(gòu)成圖6-2-4所示的二階低通濾波器。
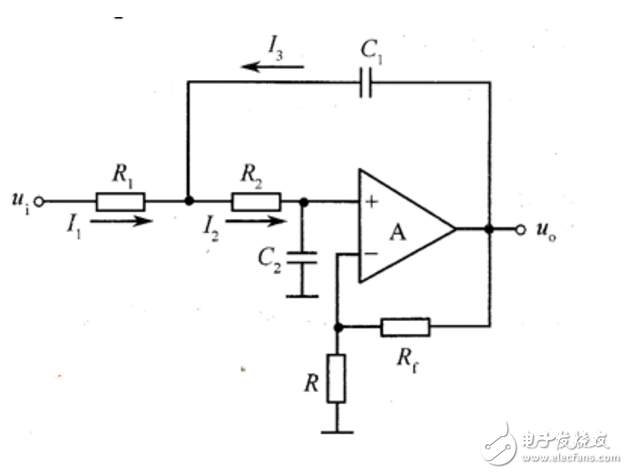
對于上圖所示的二階低通濾波器,其傳遞函數(shù)為

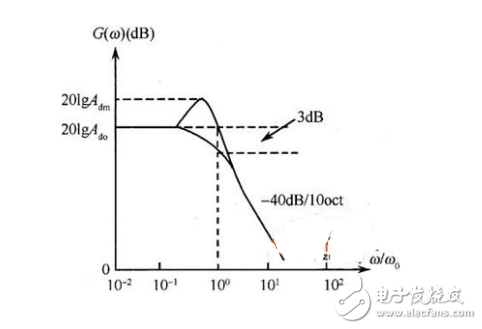
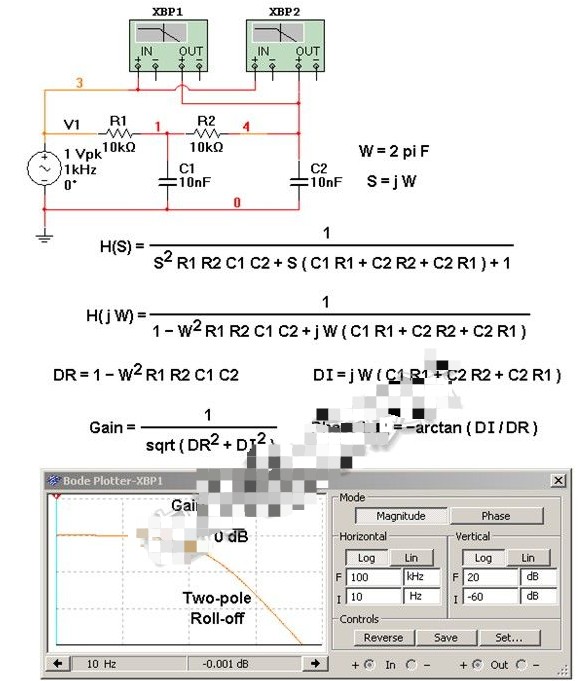
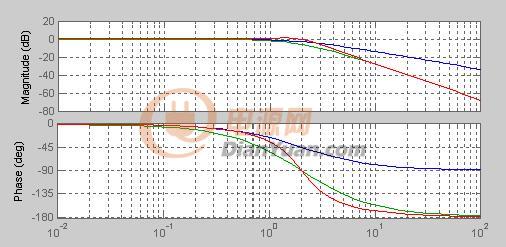
如圖6-2-5所示為二階低通濾波器的幅頻特性曲線,其阻帶衰減特性的斜率為-40dB/10oct,克服了一階低通濾波器阻帶衰減太慢的缺點(diǎn)。
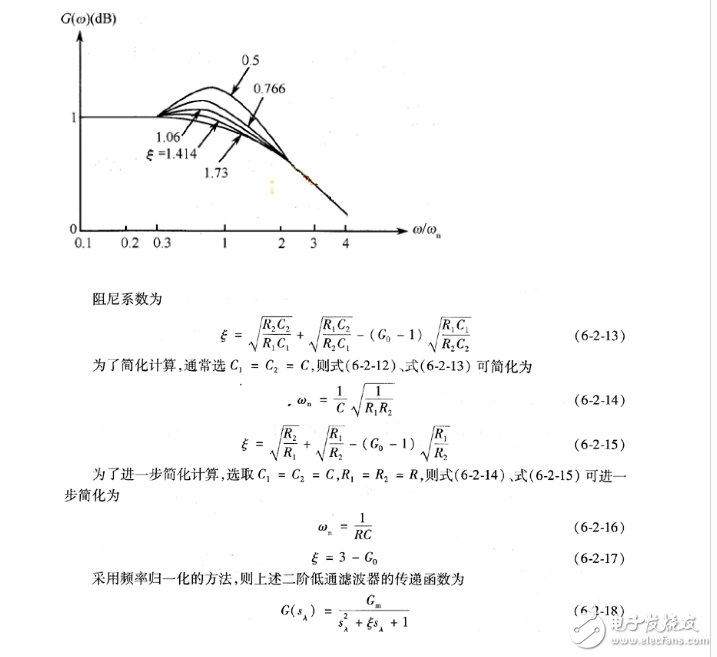
二階低通濾波器的各個(gè)參數(shù),影響其濾波特性,如阻尼系數(shù)苫的大小,決定了幅頻特性有無峰值,或諧振峰的高低。如圖6=2-6所示為苫對二階低通濾波器幅頻特性的影響。
由傳遞函數(shù)判斷濾波器
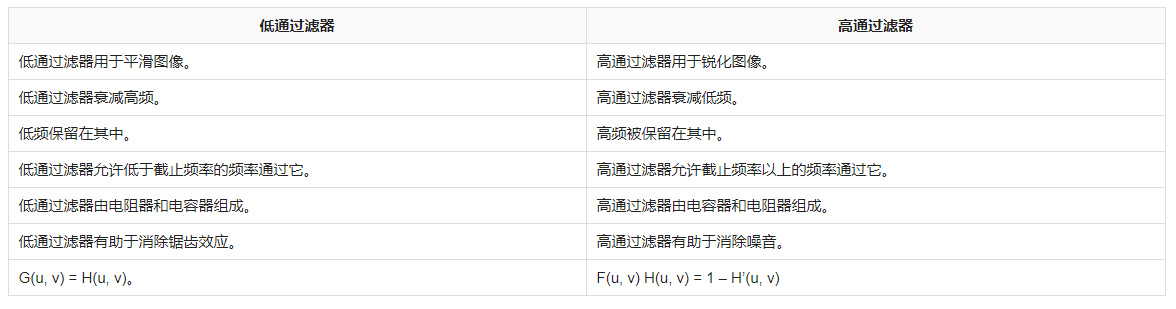
根據(jù)系統(tǒng)函數(shù)快速判斷濾波器類型
(1)死辦法,用傅里葉變換求出H(f),在畫出幅頻特性曲線,看高頻部分是不是“通”
(2)用拉氏變換求出H(s),然后記住一句話:分子上有什么就通什么!
舉個(gè)例子:
H(s)=as/(bs+c)
分子上有“高次”,所以是高通。
這里的“高次”是這個(gè)意思:
分母上有s的0次和1次,分子是s的1次,所以是較高的那個(gè),簡稱“高次”。
H(s)=a/(bs+c)
分子上有“低次”,所以是低通。
H(s)=as^2/(bs^2+cs+d)
分子上有“高次”,所以是高通。
H(s)=a/(bs^2+cs+d)
分子上有“低次”,所以是低通。
H(s)=as/(bs^2+cs+d)
分子上有“中間次”,所以是帶通。
第(2)種方法還沒找到理論根據(jù),如果將分子分母都除以“高次”,在判斷頻率從小變化到無窮的情況能理解
如果只有一個(gè)零極點(diǎn),可以根據(jù)復(fù)平面上零極點(diǎn)位置來判斷。
 電子發(fā)燒友App
電子發(fā)燒友App








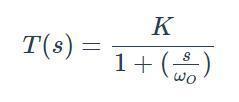
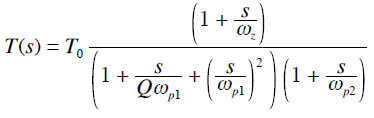
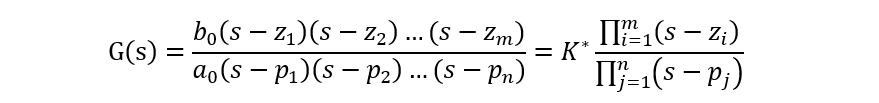
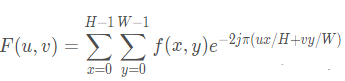




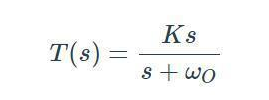












評論