任何一本信號(hào)與系統(tǒng)的教材上,都有這樣一個(gè)結(jié)論:
LTI系統(tǒng)穩(wěn)定性的充要條件是:?jiǎn)挝粵_激響應(yīng)h(t)/h(n)絕對(duì)可積/絕對(duì)可和。但是,理想低通濾波器呢?它是不是穩(wěn)定系統(tǒng)?如果是,它的單位沖激響應(yīng)滿足絕對(duì)可積嗎?如果不是,能找到一個(gè)有界的輸入,通過理想低通,產(chǎn)生無界的輸出嗎?
下面是廈門理工學(xué)院唐駿老師的一篇舊文,此惑一直未解,歡迎大家討論。
以下試卷摘自《信號(hào)與系統(tǒng)學(xué)習(xí)指導(dǎo)》:
選擇題第4題所給的參考答案是B,即說明理想低通濾波器是穩(wěn)定的,這一點(diǎn)似乎沒什么疑問?!
以下摘自《信號(hào)與系統(tǒng)》第二版 奧本海姆 劉樹棠 譯
(6.19)式并非絕對(duì)可積,關(guān)于這一點(diǎn),可參考《數(shù)字信號(hào)處理理論、算法與實(shí)現(xiàn)》第二版 胡廣書 P96,摘抄如下:
綜上可以得出以下兩個(gè)結(jié)論:
1、低通濾波器是穩(wěn)定的;
2、其單位沖激響應(yīng)h(t)是平方可積的,但不是絕對(duì)可積的。
然而,在幾乎所有的信號(hào)與系統(tǒng)的教材中都有如下結(jié)論:
LTI系統(tǒng)穩(wěn)定的充要條件是:?jiǎn)挝粵_激響應(yīng)絕對(duì)可積或單位脈沖響應(yīng)絕對(duì)可和。
以下摘自《信號(hào)與系統(tǒng)》第二版奧本海姆 劉樹棠 譯 P82:
以下摘自《信號(hào)與系統(tǒng)性系統(tǒng)分析》第四版吳大正 P339:
通過以上分析,有關(guān)LTI系統(tǒng)穩(wěn)定條件是否應(yīng)該作修改?還是分析過程中有不對(duì)之處?
以上為唐老師原文。我查閱了一下數(shù)字信號(hào)處理的書籍,對(duì)于離散時(shí)間系統(tǒng),也有相同的結(jié)論。以下為為程佩青《數(shù)字信號(hào)處理第四版》清華大學(xué)出版社P30頁。
下面是書中P96和P97頁,闡述了絕對(duì)可和與平方可和的區(qū)別,也明確指出,理想低通濾波器的單位沖激響應(yīng)h(n)不滿足絕對(duì)可和,滿足平方可和。但書中未分析其穩(wěn)定性。
那么,理想低通濾波器,到底是不是穩(wěn)定系統(tǒng)呢?歡迎大家來討論。
-
濾波器
+關(guān)注
關(guān)注
162文章
8066瀏覽量
181005 -
LTI
+關(guān)注
關(guān)注
0文章
11瀏覽量
10556
原文標(biāo)題:關(guān)于LTI系統(tǒng)穩(wěn)定性充要條件的一個(gè)疑問
文章出處:【微信號(hào):SignalAndSystem_DSP,微信公眾號(hào):信號(hào)與系統(tǒng)和數(shù)字信號(hào)處理】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
低通濾波器設(shè)計(jì)

LC低通濾波器作用及應(yīng)用案例
數(shù)字低通濾波器的設(shè)計(jì)

基于MATLAB的理想低通濾波器的設(shè)計(jì)
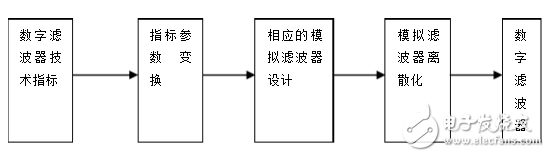
LTCC低通濾波器的設(shè)計(jì)解析
低通濾波器的設(shè)計(jì)與實(shí)現(xiàn)
Matlab低通濾波器設(shè)定與實(shí)踐

低通濾波器與高通濾波器有什么不同
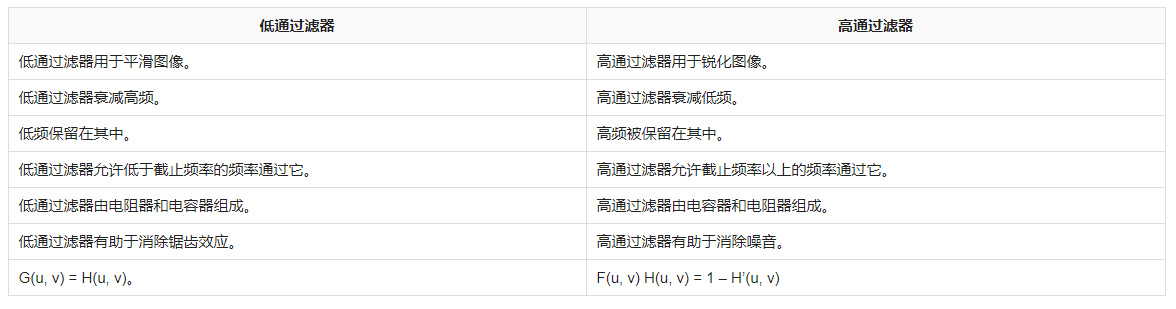
高通濾波器和低通濾波器的關(guān)系
低通濾波器電路圖分享
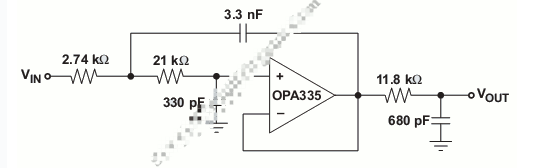
有源低通濾波器設(shè)計(jì)原理 有源低通濾波器的截止頻率計(jì)算
低通濾波器的作用 低通濾波器的帶寬怎么看
高通濾波器、低通濾波器、帶通濾波器怎樣測(cè)幅頻特性?
什么是低通濾波器?低通濾波器有什么作用?






 理想低通濾波器,是穩(wěn)定系統(tǒng)嗎?
理想低通濾波器,是穩(wěn)定系統(tǒng)嗎?










評(píng)論