Zeptolab數(shù)據(jù)科學(xué)家Dmitriy Sergeev介紹了分析和預(yù)測(cè)時(shí)序數(shù)據(jù)的主要方法。
大家好!
這次的開(kāi)放機(jī)器學(xué)習(xí)課程的內(nèi)容是時(shí)序數(shù)據(jù)。
我們將查看如何使用Python處理時(shí)序數(shù)據(jù),哪些方法和模型可以用來(lái)預(yù)測(cè);什么是雙指數(shù)平滑和三指數(shù)平滑;如果平穩(wěn)(stationarity)不是你的菜,該怎么辦;如何創(chuàng)建SARIMA并且活下來(lái);如何使用XGBoost做出預(yù)測(cè)。所有這些都將應(yīng)用于(嚴(yán)酷的)真實(shí)世界例子。
導(dǎo)言
在我的工作中,我?guī)缀趺刻於紩?huì)碰到和時(shí)序有關(guān)的任務(wù)。最頻繁的問(wèn)題是——明天/下一周/下個(gè)月/等等,我們的指標(biāo)將是什么樣——有多少玩家會(huì)安裝應(yīng)用,他們的在線時(shí)長(zhǎng)會(huì)是多少,他們會(huì)進(jìn)行多少次操作,取決于預(yù)測(cè)所需的質(zhì)量,預(yù)測(cè)周期的長(zhǎng)度,以及時(shí)刻,我們需要選擇特征,調(diào)整參數(shù),以取得所需結(jié)果。
基本定義
時(shí)序的簡(jiǎn)單定義:
時(shí)序——一系列以時(shí)間順序?yàn)?a target="_blank">索引(或列出、繪出)的數(shù)據(jù)點(diǎn)。
因此,數(shù)據(jù)以相對(duì)確定的時(shí)刻組織。所以,和隨機(jī)樣本相比,可能包含我們將嘗試提取的額外信息。
讓我們導(dǎo)入一些庫(kù)。首先我們需要statsmodels庫(kù),它包含了一大堆統(tǒng)計(jì)學(xué)建模函數(shù),包括時(shí)序。對(duì)不得不遷移到Python的R粉來(lái)說(shuō),絕對(duì)會(huì)感到statsmodels很熟悉,因?yàn)樗С诸愃芖age ~ Age + Education這樣的模型定義。
import numpy as np # 向量和矩陣
import pandas as pd # 表格和數(shù)據(jù)處理
import matplotlib.pyplot as plt # 繪圖
import seaborn as sns # 更多繪圖功能
from dateutil.relativedelta import relativedelta # 處理不同格式的時(shí)間日期
from scipy.optimize import minimize # 最小化函數(shù)
import statsmodels.formula.api as smf # 統(tǒng)計(jì)學(xué)和計(jì)量經(jīng)濟(jì)學(xué)
import statsmodels.tsa.api as smt
import statsmodels.api as sm
import scipy.stats as scs
from itertools import product # 一些有用的函數(shù)
from tqdm import tqdm_notebook
import warnings # 勿擾模式
warnings.filterwarnings('ignore')
%matplotlib inline
作為例子,讓我們使用一些真實(shí)的手游數(shù)據(jù),玩家每小時(shí)觀看的廣告,以及每天游戲幣的花費(fèi):
ads = pd.read_csv('../../data/ads.csv', index_col=['Time'], parse_dates=['Time'])
currency = pd.read_csv('../../data/currency.csv', index_col=['Time'], parse_dates=['Time'])
plt.figure(figsize=(15, 7))
plt.plot(ads.Ads)
plt.title('Ads watched (hourly data)')
plt.grid(True)
plt.show()
plt.figure(figsize=(15, 7))
plt.plot(currency.GEMS_GEMS_SPENT)
plt.title('In-game currency spent (daily data)')
plt.grid(True)
plt.show()
預(yù)測(cè)質(zhì)量指標(biāo)
在實(shí)際開(kāi)始預(yù)測(cè)之前,先讓我們理解下如何衡量預(yù)測(cè)的質(zhì)量,查看下最常見(jiàn)、使用最廣泛的測(cè)度:
R2,決定系數(shù)(在經(jīng)濟(jì)學(xué)中,可以理解為模型能夠解釋的方差比例),(-inf, 1]sklearn.metrics.r2_score
平均絕對(duì)誤差(Mean Absolute Error),這是一個(gè)易于解釋的測(cè)度,因?yàn)樗挠?jì)量單位和初始序列相同,[0, +inf)sklearn.metrics.mean_absolute_error
中位絕對(duì)誤差(Median Absolute Error),同樣是一個(gè)易于解釋的測(cè)度,對(duì)離群值的魯棒性很好,[0, +inf)sklearn.metrics.median_absolute_error
均方誤差(Mean Squared Error),最常用的測(cè)度,給較大的錯(cuò)誤更高的懲罰,[0, +inf)sklearn.metrics.mean_squared_error
均方對(duì)數(shù)誤差(Mean Squared Logarithmic Error),和MSE差不多,只不過(guò)先對(duì)序列取對(duì)數(shù),因此能夠照顧到較小的錯(cuò)誤,通常用于具有指數(shù)趨勢(shì)的數(shù)據(jù),[0, +inf)sklearn.metrics.mean_squared_log_error
平均絕對(duì)百分誤差(Mean Absolute Percentage Error),類似MAE不過(guò)基于百分比——當(dāng)你需要向管理層解釋模型的質(zhì)量時(shí)很方便——[0, +inf),sklearn中沒(méi)有實(shí)現(xiàn)。
# 引入上面提到的所有測(cè)度
from sklearn.metrics import r2_score, median_absolute_error, mean_absolute_error
from sklearn.metrics import median_absolute_error, mean_squared_error, mean_squared_log_error
# 自行實(shí)現(xiàn)sklearn沒(méi)有提供的平均絕對(duì)百分誤差很容易
def mean_absolute_percentage_error(y_true, y_pred):
return np.mean(np.abs((y_true - y_pred) / y_true)) * 100
棒極了,現(xiàn)在我們知道如何測(cè)量預(yù)測(cè)的質(zhì)量了,可以使用哪些測(cè)度,以及如何向老板翻譯結(jié)果。剩下的就是創(chuàng)建模型了。
平移、平滑、評(píng)估
讓我們從一個(gè)樸素的假設(shè)開(kāi)始——“明天會(huì)和今天一樣”,但是我們并不使用類似y^t=y(t-1)這樣的模型(這其實(shí)是一個(gè)適用于任意時(shí)序預(yù)測(cè)問(wèn)題的很好的基線,有時(shí)任何模型都無(wú)法戰(zhàn)勝這一模型),相反,我們將假定變量未來(lái)的值取決于前n個(gè)值的平均,所以我們將使用的是移動(dòng)平均(moving average)。
def moving_average(series, n):
"""
計(jì)算前n項(xiàng)觀測(cè)的平均數(shù)
"""
return np.average(series[-n:])
# 根據(jù)前24小時(shí)的數(shù)據(jù)預(yù)測(cè)
moving_average(ads, 24)
結(jié)果:116805.0
不幸的是這樣我們無(wú)法做出長(zhǎng)期預(yù)測(cè)——為了預(yù)測(cè)下一步的數(shù)據(jù)我們需要實(shí)際觀測(cè)的之前的數(shù)據(jù)。不過(guò)移動(dòng)平均還有一種用途——平滑原時(shí)序以顯示趨勢(shì)。pandas提供了實(shí)現(xiàn)DataFrame.rolling(window).mean()。窗口越寬,趨勢(shì)就越平滑。遇到噪聲很大的數(shù)據(jù)時(shí)(財(cái)經(jīng)數(shù)據(jù)十分常見(jiàn)),這一過(guò)程有助于偵測(cè)常見(jiàn)模式。
def plotMovingAverage(series, window, plot_intervals=False, scale=1.96, plot_anomalies=False):
"""
series - 時(shí)序dateframe
window - 滑窗大小
plot_intervals - 顯示置信區(qū)間
plot_anomalies - 顯示異常值
"""
rolling_mean = series.rolling(window=window).mean()
plt.figure(figsize=(15,5))
plt.title("Moving average window size = {}".format(window))
plt.plot(rolling_mean, "g", label="Rolling mean trend")
# 繪制平滑后的數(shù)據(jù)的置信區(qū)間
if plot_intervals:
mae = mean_absolute_error(series[window:], rolling_mean[window:])
deviation = np.std(series[window:] - rolling_mean[window:])
lower_bond = rolling_mean - (mae + scale * deviation)
upper_bond = rolling_mean + (mae + scale * deviation)
plt.plot(upper_bond, "r--", label="Upper Bond / Lower Bond")
plt.plot(lower_bond, "r--")
# 得到區(qū)間后,找出異常值
if plot_anomalies:
anomalies = pd.DataFrame(index=series.index, columns=series.columns)
anomalies[series
anomalies[series>upper_bond] = series[series>upper_bond]
plt.plot(anomalies, "ro", markersize=10)
plt.plot(series[window:], label="Actual values")
plt.legend(loc="upper left")
plt.grid(True)
平滑(窗口大小為4小時(shí)):
plotMovingAverage(ads, 4)
平滑(窗口大小為12小時(shí)):
plotMovingAverage(ads, 12)
平滑(窗口大小為24小時(shí)):
plotMovingAverage(ads, 24)
如你所見(jiàn),在小時(shí)數(shù)據(jù)上按日平滑讓我們可以清楚地看到瀏覽廣告的趨勢(shì)。周末數(shù)值較高(周末是娛樂(lè)時(shí)間),工作日一般數(shù)值較低。
我們可以同時(shí)繪制平滑值的置信區(qū)間:
plotMovingAverage(ads, 4, plot_intervals=True)
現(xiàn)在讓我們?cè)谝苿?dòng)平均的幫助下創(chuàng)建一個(gè)簡(jiǎn)單的異常檢測(cè)系統(tǒng)。不幸的是,在這段時(shí)序數(shù)據(jù)中,一切都比較正常,所以讓我們故意弄出點(diǎn)異常來(lái):
ads_anomaly = ads.copy()
# 例如廣告瀏覽量下降了20%
ads_anomaly.iloc[-20] = ads_anomaly.iloc[-20] * 0.2
讓我們看看這個(gè)簡(jiǎn)單的方法能不能捕獲異常:
plotMovingAverage(ads_anomaly, 4, plot_intervals=True, plot_anomalies=True)
酷!按周平滑呢?
plotMovingAverage(currency, 7, plot_intervals=True, plot_anomalies=True)
不好!這是簡(jiǎn)單方法的缺陷——它沒(méi)能捕捉月度數(shù)據(jù)的季節(jié)性,幾乎將所有30天出現(xiàn)一次的峰值當(dāng)作異常值。如果你不想有這么多虛假警報(bào),最好考慮更復(fù)雜的模型。
順便提下移動(dòng)平均的一個(gè)簡(jiǎn)單修正——加權(quán)平均(weighted average)。其中不同的觀測(cè)具有不同的權(quán)重,所有權(quán)重之和為一。通常最近的觀測(cè)具有較高的權(quán)重。
def weighted_average(series, weights):
result = 0.0
weights.reverse()
for n in range(len(weights)):
result += series.iloc[-n-1] * weights[n]
return float(result)
weighted_average(ads, [0.6, 0.3, 0.1])
結(jié)果:98423.0
指數(shù)平滑
那么,如果我們不只加權(quán)最近的幾項(xiàng)觀測(cè),而是加權(quán)全部現(xiàn)有的觀測(cè),但對(duì)歷史數(shù)據(jù)的權(quán)重應(yīng)用指數(shù)下降呢?
這一模型的值是當(dāng)前觀測(cè)和歷史觀測(cè)的加權(quán)平均。權(quán)重α稱為平滑因子,定義多快“遺忘”之前的觀測(cè)。α越小,之前的值的影響就越大,序列就越平滑。
指數(shù)隱藏在函數(shù)的遞歸調(diào)用之中,y^t-1本身包含(1-α)y^t-2,以此類推,直到序列的開(kāi)始。
def exponential_smoothing(series, alpha):
"""
series - 時(shí)序數(shù)據(jù)集
alpha - 浮點(diǎn)數(shù),范圍[0.0, 1.0],平滑參數(shù)
"""
result = [series[0]] # 第一項(xiàng)和序列第一項(xiàng)相同
for n in range(1, len(series)):
result.append(alpha * series[n] + (1 - alpha) * result[n-1])
return result
def plotExponentialSmoothing(series, alphas):
with plt.style.context('seaborn-white'):
plt.figure(figsize=(15, 7))
for alpha in alphas:
plt.plot(exponential_smoothing(series, alpha), label="Alpha {}".format(alpha))
plt.plot(series.values, "c", label = "Actual")
plt.legend(loc="best")
plt.axis('tight')
plt.title("Exponential Smoothing")
plt.grid(True);
plotExponentialSmoothing(ads.Ads, [0.3, 0.05])
plotExponentialSmoothing(currency.GEMS_GEMS_SPENT, [0.3, 0.05])
雙指數(shù)平滑
目前我們的方法能給出的只是單個(gè)未來(lái)數(shù)據(jù)點(diǎn)的預(yù)測(cè)(以及一些良好的平滑),這很酷,但還不夠,所以讓我們擴(kuò)展下指數(shù)平滑以預(yù)測(cè)兩個(gè)未來(lái)數(shù)據(jù)點(diǎn)(當(dāng)然,同樣經(jīng)過(guò)平滑)。
序列分解應(yīng)該能幫到我們——我們得到兩個(gè)分量:截距(也叫水平)l和趨勢(shì)(也叫斜率)b。我們使用之前提到的方法學(xué)習(xí)預(yù)測(cè)截距(或期望的序列值),并將同樣的指數(shù)平滑應(yīng)用于趨勢(shì)(假定時(shí)序未來(lái)改變的方向取決于之前的加權(quán)變化)。
上面的第一個(gè)函數(shù)描述截距,和之前一樣,它取決于序列的當(dāng)前值,只不過(guò)第二項(xiàng)現(xiàn)在分成水平和趨勢(shì)兩個(gè)分量。第二個(gè)函數(shù)描述趨勢(shì),它取決于當(dāng)前一步的水平變動(dòng),以及之前的趨勢(shì)值。這里β系數(shù)是指數(shù)平滑的權(quán)重。最后的預(yù)測(cè)為模型對(duì)截距和趨勢(shì)的預(yù)測(cè)之和。
def double_exponential_smoothing(series, alpha, beta):
result = [series[0]]
for n in range(1, len(series)+1):
if n == 1:
level, trend = series[0], series[1] - series[0]
if n >= len(series):
value = result[-1]
else:
value = series[n]
last_level, level = level, alpha*value + (1-alpha)*(level+trend)
trend = beta*(level-last_level) + (1-beta)*trend
result.append(level+trend)
return result
def plotDoubleExponentialSmoothing(series, alphas, betas):
with plt.style.context('seaborn-white'):
plt.figure(figsize=(20, 8))
for alpha in alphas:
for beta in betas:
plt.plot(double_exponential_smoothing(series, alpha, beta), label="Alpha {}, beta {}".format(alpha, beta))
plt.plot(series.values, label = "Actual")
plt.legend(loc="best")
plt.axis('tight')
plt.title("Double Exponential Smoothing")
plt.grid(True)
plotDoubleExponentialSmoothing(ads.Ads, alphas=[0.9, 0.02], betas=[0.9, 0.02])
plotDoubleExponentialSmoothing(currency.GEMS_GEMS_SPENT, alphas=[0.9, 0.02], betas=[0.9, 0.02])
現(xiàn)在我們有兩個(gè)可供調(diào)節(jié)的參數(shù)——α和β。前者根據(jù)趨勢(shì)平滑序列,后者平滑趨勢(shì)本身。這兩個(gè)參數(shù)越大,最新的觀測(cè)的權(quán)重就越高,建模的序列就越不平滑。這兩個(gè)參數(shù)的組合可能產(chǎn)生非常怪異的結(jié)果,特別是手工設(shè)置時(shí)。我們很快將查看自動(dòng)選擇參數(shù)的方法,在介紹三次指數(shù)平滑之后。
Holt-Winters模型
好哇!讓我們看下一個(gè)指數(shù)平滑的變體,這次是三次指數(shù)平滑。
這一方法的思路是我們加入第三個(gè)分量——季節(jié)性。這意味著,如果我們的時(shí)序不具有季節(jié)性(我們之前的例子就不具季節(jié)性),我們就不應(yīng)該使用這一方法。模型中的季節(jié)分量將根據(jù)季節(jié)長(zhǎng)度解釋截距和趨勢(shì)上的重復(fù)波動(dòng),季節(jié)長(zhǎng)度也就是波動(dòng)重復(fù)的周期。季節(jié)中的每項(xiàng)觀測(cè)有一個(gè)單獨(dú)的分量,例如,如果季節(jié)長(zhǎng)度為7(按周計(jì)的季節(jié)),我們將有7個(gè)季節(jié)分量,每個(gè)季節(jié)分量對(duì)應(yīng)一天。
現(xiàn)在我們得到了一個(gè)新系統(tǒng):
現(xiàn)在,截?cái)嗳Q于時(shí)序的當(dāng)前值減去相應(yīng)的季節(jié)分量,趨勢(shì)沒(méi)有變動(dòng),季節(jié)分量取決于時(shí)序的當(dāng)前值減去截?cái)啵约扒耙粋€(gè)季節(jié)分量的值。注意分量在所有現(xiàn)有的季節(jié)上平滑,例如,周一分量會(huì)和其他所有周一平均。關(guān)于如何計(jì)算平均以及趨勢(shì)分量和季節(jié)分量的初始逼近,可以參考工程統(tǒng)計(jì)手冊(cè)6.4.3.5:
https://www.itl.nist.gov/div898/handbook/pmc/section4/pmc435.htm
具備季節(jié)分量后,我們可以預(yù)測(cè)任意m步未來(lái),而不是一步或兩步,非常鼓舞人心。
下面是三次指數(shù)平滑模型的代碼,也稱Holt-Winters模型,得名于發(fā)明人的姓氏——Charles Holt和他的學(xué)生Peter Winters。此外,模型中還引入了Brutlag方法,以創(chuàng)建置信區(qū)間:
其中T為季節(jié)的長(zhǎng)度,d為預(yù)測(cè)偏差。你可以參考以下論文了解這一方法的更多內(nèi)容,以及它在時(shí)序異常檢測(cè)中的應(yīng)用:
https://annals-csis.org/proceedings/2012/pliks/118.pdf
classHoltWinters:
"""
Holt-Winters模型,使用Brutlag方法檢測(cè)異常
# series - 初始時(shí)序
# slen - 季節(jié)長(zhǎng)度
# alpha, beta, gamma - Holt-Winters模型參數(shù)
# n_preds - 預(yù)測(cè)視野
# scaling_factor - 設(shè)置Brutlag方法的置信區(qū)間(通常位于2到3之間)
"""
def __init__(self, series, slen, alpha, beta, gamma, n_preds, scaling_factor=1.96):
self.series = series
self.slen = slen
self.alpha = alpha
self.beta = beta
self.gamma = gamma
self.n_preds = n_preds
self.scaling_factor = scaling_factor
def initial_trend(self):
sum = 0.0
for i in range(self.slen):
sum += float(self.series[i+self.slen] - self.series[i]) / self.slen
return sum / self.slen
def initial_seasonal_components(self):
seasonals = {}
season_averages = []
n_seasons = int(len(self.series)/self.slen)
# 計(jì)算季節(jié)平均
for j in range(n_seasons):
season_averages.append(sum(self.series[self.slen*j:self.slen*j+self.slen])/float(self.slen))
# 計(jì)算初始值
for i in range(self.slen):
sum_of_vals_over_avg = 0.0
for j in range(n_seasons):
sum_of_vals_over_avg += self.series[self.slen*j+i]-season_averages[j]
seasonals[i] = sum_of_vals_over_avg/n_seasons
return seasonals
def triple_exponential_smoothing(self):
self.result = []
self.Smooth = []
self.Season = []
self.Trend = []
self.PredictedDeviation = []
self.UpperBond = []
self.LowerBond = []
seasonals = self.initial_seasonal_components()
for i in range(len(self.series)+self.n_preds):
if i == 0: # 成分初始化
smooth = self.series[0]
trend = self.initial_trend()
self.result.append(self.series[0])
self.Smooth.append(smooth)
self.Trend.append(trend)
self.Season.append(seasonals[i%self.slen])
self.PredictedDeviation.append(0)
self.UpperBond.append(self.result[0] +
self.scaling_factor *
self.PredictedDeviation[0])
self.LowerBond.append(self.result[0] -
self.scaling_factor *
self.PredictedDeviation[0])
continue
if i >= len(self.series): # 預(yù)測(cè)
m = i - len(self.series) + 1
self.result.append((smooth + m*trend) + seasonals[i%self.slen])
# 預(yù)測(cè)時(shí)在每一步增加不確定性
self.PredictedDeviation.append(self.PredictedDeviation[-1]*1.01)
else:
val = self.series[i]
last_smooth, smooth = smooth, self.alpha*(val-seasonals[i%self.slen]) + (1-self.alpha)*(smooth+trend)
trend = self.beta * (smooth-last_smooth) + (1-self.beta)*trend
seasonals[i%self.slen] = self.gamma*(val-smooth) + (1-self.gamma)*seasonals[i%self.slen]
self.result.append(smooth+trend+seasonals[i%self.slen])
# 據(jù)Brutlag算法計(jì)算偏差
self.PredictedDeviation.append(self.gamma * np.abs(self.series[i] - self.result[i])
+ (1-self.gamma)*self.PredictedDeviation[-1])
self.UpperBond.append(self.result[-1] +
self.scaling_factor *
self.PredictedDeviation[-1])
self.LowerBond.append(self.result[-1] -
self.scaling_factor *
self.PredictedDeviation[-1])
self.Smooth.append(smooth)
self.Trend.append(trend)
self.Season.append(seasonals[i%self.slen])
時(shí)序交叉驗(yàn)證
現(xiàn)在我們?cè)搩冬F(xiàn)之前的承諾,討論下如何自動(dòng)估計(jì)模型參數(shù)。
這里沒(méi)什么不同尋常的,我們需要選擇一個(gè)適合任務(wù)的損失函數(shù),以了解模型逼近數(shù)據(jù)的程度。接著,我們通過(guò)交叉驗(yàn)證為給定的模型參數(shù)評(píng)估選擇的交叉函數(shù),計(jì)算梯度,調(diào)整模型參數(shù),等等,勇敢地下降到誤差的全局最小值。
問(wèn)題在于如何在時(shí)序數(shù)據(jù)上進(jìn)行交叉驗(yàn)證,因?yàn)椋阒溃瑫r(shí)序數(shù)據(jù)確實(shí)具有時(shí)間結(jié)構(gòu),不能在一折中隨機(jī)混合數(shù)據(jù)(不保留時(shí)間結(jié)構(gòu)),否則觀測(cè)間的所有時(shí)間相關(guān)性都會(huì)丟失。這就是為什么我們將使用技巧性更強(qiáng)的方法來(lái)優(yōu)化模型參數(shù)的原因。我不知道這個(gè)方法是否有正式的名稱,但是在CrossValidated上(在這個(gè)網(wǎng)站上你可以找到所有問(wèn)題的答案,生命、宇宙以及任何事情的終極答案除外),有人提出了“滾動(dòng)式交叉驗(yàn)證”(cross-validation on a rolling basis)這一名稱。
這一想法很簡(jiǎn)單——我們?cè)跁r(shí)序數(shù)據(jù)的一小段上訓(xùn)練模型,從時(shí)序開(kāi)始到某一時(shí)刻t,預(yù)測(cè)接下來(lái)的t+n步并計(jì)算誤差。接著擴(kuò)張訓(xùn)練樣本至t+n個(gè)值,并預(yù)測(cè)從t+n到t+2×n的數(shù)據(jù)。持續(xù)擴(kuò)張直到窮盡所有觀測(cè)。初始訓(xùn)練樣本到最后的觀測(cè)之間可以容納多少個(gè)n,我們就可以進(jìn)行多少折交叉驗(yàn)證。
了解了如何設(shè)置交叉驗(yàn)證,我們將找出Holt-Winters模型的最優(yōu)參數(shù),回憶一下,我們的廣告數(shù)據(jù)有按日季節(jié)性,所以我們有slen=24。
from sklearn.model_selection importTimeSeriesSplit
def timeseriesCVscore(params, series, loss_function=mean_squared_error, slen=24):
errors = []
values = series.values
alpha, beta, gamma = params
# 設(shè)定交叉驗(yàn)證折數(shù)
tscv = TimeSeriesSplit(n_splits=3)
for train, test in tscv.split(values):
model = HoltWinters(series=values[train], slen=slen,
alpha=alpha, beta=beta, gamma=gamma, n_preds=len(test))
model.triple_exponential_smoothing()
predictions = model.result[-len(test):]
actual = values[test]
error = loss_function(predictions, actual)
errors.append(error)
return np.mean(np.array(errors))
和其他指數(shù)平滑模型一樣,Holt-Winters模型中,平滑參數(shù)的取值范圍在0到1之間,因此我們需要選擇一種支持給模型參數(shù)添加限制的算法。我們選擇了截?cái)嗯nD共軛梯度(Truncated Newton conjugate gradient)。
data = ads.Ads[:-20] # 留置一些數(shù)據(jù)用于測(cè)試
# 初始化模型參數(shù)alpha、beta、gamma
x = [0, 0, 0]
# 最小化損失函數(shù)
opt = minimize(timeseriesCVscore, x0=x,
args=(data, mean_squared_log_error),
method="TNC", bounds = ((0, 1), (0, 1), (0, 1))
)
# 取最優(yōu)值……
alpha_final, beta_final, gamma_final = opt.x
print(alpha_final, beta_final, gamma_final)
# ……并據(jù)此訓(xùn)練模型,預(yù)測(cè)接下來(lái)50個(gè)小時(shí)的數(shù)據(jù)
model = HoltWinters(data, slen = 24,
alpha = alpha_final,
beta = beta_final,
gamma = gamma_final,
n_preds = 50, scaling_factor = 3)
model.triple_exponential_smoothing()
最優(yōu)參數(shù):
0.116526802273504540.0026776974311058520.05820973606789237
繪圖部分的代碼:
def plotHoltWinters(series, plot_intervals=False, plot_anomalies=False):
"""
series - 時(shí)序數(shù)據(jù)集
plot_intervals - 顯示置信區(qū)間
plot_anomalies - 顯示異常值
"""
plt.figure(figsize=(20, 10))
plt.plot(model.result, label = "Model")
plt.plot(series.values, label = "Actual")
error = mean_absolute_percentage_error(series.values, model.result[:len(series)])
plt.title("Mean Absolute Percentage Error: {0:.2f}%".format(error))
if plot_anomalies:
anomalies = np.array([np.NaN]*len(series))
anomalies[series.values
series.values[series.values
anomalies[series.values>model.UpperBond[:len(series)]] =
series.values[series.values>model.UpperBond[:len(series)]]
plt.plot(anomalies, "o", markersize=10, label = "Anomalies")
if plot_intervals:
plt.plot(model.UpperBond, "r--", alpha=0.5, label = "Up/Low confidence")
plt.plot(model.LowerBond, "r--", alpha=0.5)
plt.fill_between(x=range(0,len(model.result)), y1=model.UpperBond,
y2=model.LowerBond, alpha=0.2, color = "grey")
plt.vlines(len(series), ymin=min(model.LowerBond), ymax=max(model.UpperBond), linestyles='dashed')
plt.axvspan(len(series)-20, len(model.result), alpha=0.3, color='lightgrey')
plt.grid(True)
plt.axis('tight')
plt.legend(loc="best", fontsize=13);
plotHoltWinters(ads.Ads)
plotHoltWinters(ads.Ads, plot_intervals=True, plot_anomalies=True)
上面的圖形表明,我們的模型能夠很好地逼近初始時(shí)序,捕捉每日季節(jié)性,總體的下降趨勢(shì),甚至一些異常。如果我們查看下建模偏差(見(jiàn)下圖),我們將很明顯地看到,模型對(duì)序列結(jié)構(gòu)的改變反應(yīng)相當(dāng)鮮明,但接著很快偏差就回歸正常值,“遺忘”了過(guò)去。模型的這一特性讓我們甚至可以為相當(dāng)噪雜的序列快速構(gòu)建異常檢測(cè)系統(tǒng),而無(wú)需花費(fèi)過(guò)多時(shí)間和金錢(qián)準(zhǔn)備數(shù)據(jù)和訓(xùn)練模型。
plt.figure(figsize=(25, 5))
plt.plot(model.PredictedDeviation)
plt.grid(True)
plt.axis('tight')
plt.title("Brutlag's predicted deviation");
遇到異常時(shí)偏差會(huì)增加
我們將在第二個(gè)序列上應(yīng)用相同的算法,我們知道,第二個(gè)序列具有趨勢(shì)和每月季節(jié)性。
data = currency.GEMS_GEMS_SPENT[:-50]
slen = 30
x = [0, 0, 0]
opt = minimize(timeseriesCVscore, x0=x,
args=(data, mean_absolute_percentage_error, slen),
method="TNC", bounds = ((0, 1), (0, 1), (0, 1))
)
alpha_final, beta_final, gamma_final = opt.x
model = HoltWinters(data, slen = slen,
alpha = alpha_final,
beta = beta_final,
gamma = gamma_final,
n_preds = 100, scaling_factor = 3)
model.triple_exponential_smoothing()
看起來(lái)很不錯(cuò),模型捕捉了向上的趨勢(shì)和季節(jié)性尖峰,總體而言很好地?cái)M合了數(shù)據(jù)。
也捕獲了一些異常
偏差隨著預(yù)測(cè)周期的推進(jìn)而上升
計(jì)量經(jīng)濟(jì)學(xué)方法
平穩(wěn)性
在開(kāi)始建模之前,我們需要提一下時(shí)序的一個(gè)重要性質(zhì):平穩(wěn)性(stationarity)。
如果過(guò)程是平穩(wěn)的,那么它的統(tǒng)計(jì)性質(zhì)不隨時(shí)間而變,也就是均值和方差不隨時(shí)間改變(方差的恒定性也稱為同方差性),同時(shí)協(xié)方差函數(shù)也不取決于時(shí)間(應(yīng)該只取決于觀測(cè)之間的距離)。Sean Abu的博客提供了一些可視化的圖片:
右邊的紅色曲線不平穩(wěn),因?yàn)榫惦S著時(shí)間增加:
這一次,右邊的紅色曲線在方差方面的運(yùn)氣不好:
最后,第i項(xiàng)和第(i+m)項(xiàng)的協(xié)方差函數(shù)不應(yīng)該是時(shí)間的函數(shù)。隨著時(shí)間推移,右邊的紅色曲線更緊了。因此,協(xié)方差不是常量。
為什么平穩(wěn)性如此重要?我們假定未來(lái)的統(tǒng)計(jì)性質(zhì)不會(huì)和現(xiàn)在觀測(cè)到的不同,在平穩(wěn)序列上做出預(yù)測(cè)很容易。大多數(shù)時(shí)序模型多多少少建模和預(yù)測(cè)這些性質(zhì)(例如均值和方差),這就是如果原序列不平穩(wěn),預(yù)測(cè)會(huì)出錯(cuò)的原因。不幸的是,我們?cè)诮炭茣?shū)以外的地方見(jiàn)到的大多數(shù)時(shí)序都是不平穩(wěn)的。不過(guò),我們可以(并且應(yīng)該)改變這一點(diǎn)。
知己知彼,百戰(zhàn)不殆。為了對(duì)抗不平穩(wěn)性,我們首先需要檢測(cè)它。我們現(xiàn)在將查看下白噪聲和隨機(jī)游走,并且了解下如何免費(fèi)從白噪聲轉(zhuǎn)到隨機(jī)游走,無(wú)需注冊(cè)和接受驗(yàn)證短信。
白噪聲圖形:
white_noise = np.random.normal(size=1000)
with plt.style.context('bmh'):
plt.figure(figsize=(15, 5))
plt.plot(white_noise)
這一通過(guò)標(biāo)準(zhǔn)正態(tài)分布生成的過(guò)程是平穩(wěn)的,以0為中心振蕩,偏差為1. 現(xiàn)在我們將基于這一過(guò)程生成一個(gè)新過(guò)程,其中相鄰值之間的關(guān)系為:xt= ρxt-1+ et
def plotProcess(n_samples=1000, rho=0):
x = w = np.random.normal(size=n_samples)
for t in range(n_samples):
x[t] = rho * x[t-1] + w[t]
with plt.style.context('bmh'):
plt.figure(figsize=(10, 3))
plt.plot(x)
plt.title("Rho {}
Dickey-Fuller p-value: {}".format(rho, round(sm.tsa.stattools.adfuller(x)[1], 3)))
for rho in [0, 0.6, 0.9, 1]:
plotProcess(rho=rho)
第一張圖上你可以看到之前的平穩(wěn)的白噪聲。第二張圖的ρ值增加到0.6,導(dǎo)致周期更寬了,但總體上還是平穩(wěn)的。第三張圖更偏離均值0,但仍以其為中心振蕩。最后,ρ值為1時(shí)我們得到了隨機(jī)游走過(guò)程——不平穩(wěn)的時(shí)序。
這是因?yàn)檫_(dá)到閾值后,時(shí)序xt= ρxt-1+ et不再回歸其均值。如果我們從等式的兩邊減去xt-1,我們將得到xt- xt-1= (ρ-1)xt-1+ et,其中等式左邊的表達(dá)式稱為一階差分(first difference)。如果ρ = 1,那么一階差分將是平穩(wěn)的白噪聲et。這一事實(shí)是時(shí)序平穩(wěn)性的迪基-福勒檢驗(yàn)(Dickey-Fuller test)的主要思想(檢驗(yàn)是否存在單位根)。如果非平穩(wěn)序列可以通過(guò)一階差分得到平穩(wěn)序列,那么這樣的序列稱為一階單整(integrated of order 1)序列。需要指出的是,一階差分并不總是足以得到平穩(wěn)序列,因?yàn)檫^(guò)程可能是d階單整且d > 1(具有多個(gè)單位根),在這樣的情形下,需要使用增廣迪基-福勒檢驗(yàn)(augmented Dickey-Fuller test)。
我們可以使用不同方法對(duì)抗不平穩(wěn)性——多階差分,移除趨勢(shì)和季節(jié)性,平滑,以及Box-Cox變換或?qū)?shù)變換。
創(chuàng)建SARIMA擺脫不平穩(wěn)性
現(xiàn)在,讓我們歷經(jīng)使序列平穩(wěn)的多層地獄,創(chuàng)建一個(gè)ARIMA模型。
def tsplot(y, lags=None, figsize=(12, 7), style='bmh'):
"""
繪制時(shí)序及其ACF(自相關(guān)性函數(shù))、PACF(偏自相關(guān)性函數(shù)),計(jì)算迪基-福勒檢驗(yàn)
y - 時(shí)序
lags - ACF、PACF計(jì)算所用的時(shí)差
"""
ifnot isinstance(y, pd.Series):
y = pd.Series(y)
with plt.style.context(style):
fig = plt.figure(figsize=figsize)
layout = (2, 2)
ts_ax = plt.subplot2grid(layout, (0, 0), colspan=2)
acf_ax = plt.subplot2grid(layout, (1, 0))
pacf_ax = plt.subplot2grid(layout, (1, 1))
y.plot(ax=ts_ax)
p_value = sm.tsa.stattools.adfuller(y)[1]
ts_ax.set_title('Time Series Analysis Plots
Dickey-Fuller: p={0:.5f}'.format(p_value))
smt.graphics.plot_acf(y, lags=lags, ax=acf_ax)
smt.graphics.plot_pacf(y, lags=lags, ax=pacf_ax)
plt.tight_layout()
tsplot(ads.Ads, lags=60)
上:時(shí)序;左下:自相關(guān)性;右下:偏自相關(guān)性
出乎意料,初始序列是平穩(wěn)的,迪基-福勒檢驗(yàn)拒絕了單位根存在的零假設(shè)。實(shí)際上,從上面的圖形本身就可以看出這一點(diǎn)——沒(méi)有可見(jiàn)的趨勢(shì),所以均值是恒定的,整個(gè)序列的方差也相對(duì)比較穩(wěn)定。在建模之前我們只需處理季節(jié)性。為此讓我們采用“季節(jié)差分”,也就是對(duì)序列進(jìn)行簡(jiǎn)單的減法操作,時(shí)差等于季節(jié)周期。
ads_diff = ads.Ads - ads.Ads.shift(24)
tsplot(ads_diff[24:], lags=60)
好多了,可見(jiàn)的季節(jié)性消失了,然而自相關(guān)函數(shù)仍然有過(guò)多顯著的時(shí)差。為了移除它們,我們將取一階差分:從序列中減去自身(時(shí)差為1)
ads_diff = ads_diff - ads_diff.shift(1)
tsplot(ads_diff[24+1:], lags=60)
完美!我們的序列看上去是難以用筆墨形容的完美!在零周圍振蕩,迪基-福勒檢驗(yàn)表明它是平穩(wěn)的,ACF中顯著的尖峰不見(jiàn)了。我們終于可以開(kāi)始建模了!
ARIMA系速成教程
我們將逐字母講解SARIMA(p,d,q)(P,D,Q,s),季節(jié)自回歸移動(dòng)平均模型(Seasonal Autoregression Moving Average model):
AR(p)—— 自回歸模型,也就是在時(shí)序自身之上回歸。基本假設(shè)是當(dāng)前序列值取決于某個(gè)(或若干個(gè))時(shí)差前的值。模型中的最大時(shí)差記為p。通過(guò)PACF圖決定初始p值——找到最大的顯著時(shí)差,之后大多數(shù)其他時(shí)差變得不顯著。
MA(q)—— 移動(dòng)平均模型。這里不討論它的細(xì)節(jié),總之它基于以下假設(shè)建模時(shí)序的誤差,當(dāng)前誤差取決于某個(gè)時(shí)差前的值(記為q)。基于和自回歸模型類似的邏輯,可以通過(guò)ACF圖找出初始值。
讓我們把這4個(gè)字母組合起來(lái):
AR(p) + MA(q) = ARMA(p,q)
這里我們得到了自回歸移動(dòng)平均模型!如果序列是平穩(wěn)的,我們可以通過(guò)這4個(gè)字母逼近這一序列。
I(d)—— d階單整。它不過(guò)是使序列平穩(wěn)所需的非季節(jié)性差分?jǐn)?shù)。在我們的例子中,它等于1,因?yàn)槲覀兪褂靡浑A差分。
加上這一字母后我們得到了ARIMA模型,可以通過(guò)非季節(jié)性差分處理非平穩(wěn)數(shù)據(jù)。
S(s)—— 這個(gè)字母代表季節(jié)性,s為序列的季節(jié)周期長(zhǎng)度。
加上最后一個(gè)字母S后,我們發(fā)現(xiàn)這最后一個(gè)字母除了s之外,還附帶了三個(gè)額外參數(shù)——(P,D,Q)。
P—— 模型的季節(jié)分量的自回歸階數(shù),同樣可以從PACF得到,但是這次需要查看季節(jié)周期長(zhǎng)度的倍數(shù)的顯著時(shí)差的數(shù)量。例如,如果周期長(zhǎng)度等于24,查看PACF發(fā)現(xiàn)第24個(gè)時(shí)差和第48個(gè)時(shí)差顯著,那么初始P值應(yīng)當(dāng)是2.
Q—— 移動(dòng)平均模型的季節(jié)分量的階數(shù),初始值的確定和P同理,只不過(guò)使用ACF圖形。
D—— 季節(jié)性單整階數(shù)。等于1或0,分別表示是否應(yīng)用季節(jié)差分。
了解了如何設(shè)置初始參數(shù)后,讓我們回過(guò)頭去重新看下最終的圖形:
p最有可能是4,因?yàn)檫@是PACF上最后一個(gè)顯著的時(shí)差,之后大多數(shù)時(shí)差變得不顯著。
d等于1,因?yàn)槲覀儾捎玫氖且浑A差分。
q大概也等于4,這可以從ACF上看出來(lái)。
P可能等于2,因?yàn)镻ACF上第24個(gè)時(shí)差和第48個(gè)時(shí)差某種程度上比較顯著。
D等于1,我們應(yīng)用了季節(jié)差分。
Q大概是1,ACF上第24個(gè)時(shí)差是顯著的,而第48個(gè)時(shí)差不顯著。
現(xiàn)在我們打算測(cè)試不同的參數(shù)組合,看看哪個(gè)是最好的:
# 設(shè)定初始值和初始范圍
ps = range(2, 5)
d=1
qs = range(2, 5)
Ps = range(0, 3)
D=1
Qs = range(0, 2)
s = 24
# 創(chuàng)建參數(shù)所有可能組合的列表
parameters = product(ps, qs, Ps, Qs)
parameters_list = list(parameters)
len(parameters_list)的結(jié)果是54,也就是說(shuō),共有54種組合。
def optimizeSARIMA(parameters_list, d, D, s):
"""
返回參數(shù)和相應(yīng)的AIC的dataframe
parameters_list - (p, q, P, Q)元組列表
d - ARIMA模型的單整階
D - 季節(jié)性單整階
s - 季節(jié)長(zhǎng)度
"""
results = []
best_aic = float("inf")
for param in tqdm_notebook(parameters_list):
# 由于有些組合不能收斂,所以需要使用try-except
try:
model=sm.tsa.statespace.SARIMAX(ads.Ads, order=(param[0], d, param[1]),
seasonal_order=(param[3], D, param[3], s)).fit(disp=-1)
except:
continue
aic = model.aic
# 保存最佳模型、AIC、參數(shù)
if aic < best_aic:
best_model = model
best_aic = aic
best_param = param
results.append([param, model.aic])
result_table = pd.DataFrame(results)
result_table.columns = ['parameters', 'aic']
# 遞增排序,AIC越低越好
result_table = result_table.sort_values(by='aic', ascending=True).reset_index(drop=True)
return result_table
result_table = optimizeSARIMA(parameters_list, d, D, s)
# 設(shè)定參數(shù)為給出最低AIC的參數(shù)組合
p, q, P, Q = result_table.parameters[0]
best_model=sm.tsa.statespace.SARIMAX(ads.Ads, order=(p, d, q),
seasonal_order=(P, D, Q, s)).fit(disp=-1)
print(best_model.summary())
讓我們查看下這一模型的殘余分量(residual):
tsplot(best_model.resid[24+1:], lags=60)
很明顯,殘余是平穩(wěn)的,沒(méi)有明顯的自相關(guān)性。
讓我們使用這一模型進(jìn)行預(yù)測(cè):
def plotSARIMA(series, model, n_steps):
"""
繪制模型預(yù)測(cè)值與實(shí)際數(shù)據(jù)對(duì)比圖
series - 時(shí)序數(shù)據(jù)集
model - SARIMA模型
n_steps - 預(yù)測(cè)未來(lái)的步數(shù)
"""
data = series.copy()
data.columns = ['actual']
data['arima_model'] = model.fittedvalues
# 平移s+d步,因?yàn)椴罘值木壒剩懊娴囊恍?shù)據(jù)沒(méi)有被模型觀測(cè)到
data['arima_model'][:s+d] = np.NaN
forecast = model.predict(start = data.shape[0], end = data.shape[0]+n_steps)
forecast = data.arima_model.append(forecast)
# 計(jì)算誤差,同樣平移s+d步
error = mean_absolute_percentage_error(data['actual'][s+d:], data['arima_model'][s+d:])
plt.figure(figsize=(15, 7))
plt.title("Mean Absolute Percentage Error: {0:.2f}%".format(error))
plt.plot(forecast, color='r', label="model")
plt.axvspan(data.index[-1], forecast.index[-1], alpha=0.5, color='lightgrey')
plt.plot(data.actual, label="actual")
plt.legend()
plt.grid(True);
plotSARIMA(ads, best_model, 50)
最終我們得到了相當(dāng)不錯(cuò)的預(yù)測(cè),模型的平均誤差率是4.01%,這非常非常好。但是為了達(dá)到這一精確度,在準(zhǔn)備數(shù)據(jù)、使序列平穩(wěn)化、暴力搜索參數(shù)上付出了太多。
時(shí)序數(shù)據(jù)上的線性(以及不那么線性)模型
在我的工作中,創(chuàng)建模型的指導(dǎo)原則常常是快、好、省。這意味著有些模型永遠(yuǎn)不會(huì)用于生產(chǎn)環(huán)境,因?yàn)樗鼈冃枰^(guò)長(zhǎng)的時(shí)間準(zhǔn)備數(shù)據(jù)(比如SARIMA),或者需要頻繁地重新訓(xùn)練新數(shù)據(jù)(比如SARIMA),或者很難調(diào)整(比如SARIMA)。相反,我經(jīng)常使用輕松得多的方法,從現(xiàn)有時(shí)序中選取一些特征,然后創(chuàng)建一個(gè)簡(jiǎn)單的線性回歸或隨機(jī)森林模型。又快又省。
也許這個(gè)方法沒(méi)有充分的理論支撐,打破了一些假定(比如,高斯-馬爾可夫定理,特別是誤差不相關(guān)的部分),但在實(shí)踐中,這很有用,在機(jī)器學(xué)習(xí)競(jìng)賽中也相當(dāng)常用。
特征提取
很好,模型需要特征,而我們所有的不過(guò)是1維時(shí)序。我們可以提取什么特征?
首先當(dāng)然是時(shí)差。
窗口統(tǒng)計(jì)量:
窗口內(nèi)序列的最大/小值
窗口的平均數(shù)/中位數(shù)
窗口的方差
等等
日期和時(shí)間特征
每小時(shí)的第幾分鐘,每天的第幾小時(shí),每周的第幾天,你懂的
這一天是節(jié)假日嗎?也許有什么特別的事情發(fā)生了?這可以作為布爾值特征
目標(biāo)編碼
其他模型的預(yù)測(cè)(不過(guò)如此預(yù)測(cè)的話會(huì)損失速度)
讓我們運(yùn)行一些模型,看看我們可以從廣告序列中提取什么
時(shí)序的時(shí)差
將序列往回移動(dòng)n步,我們能得到一個(gè)特征,其中時(shí)序的當(dāng)前值和其t-n時(shí)刻的值對(duì)齊。如果我們移動(dòng)1時(shí)差,并訓(xùn)練模型預(yù)測(cè)未來(lái),那么模型將能夠提前預(yù)測(cè)1步。增加時(shí)差,比如,增加到6,可以讓模型提前預(yù)測(cè)6步,不過(guò)它需要在觀測(cè)到數(shù)據(jù)的6步之后才能利用。如果在這期間序列發(fā)生了根本性的變動(dòng),那么模型無(wú)法捕捉這一變動(dòng),會(huì)返回誤差很大的預(yù)測(cè)。因此,時(shí)差的選取需要平衡預(yù)測(cè)的質(zhì)量和時(shí)長(zhǎng)。
data = pd.DataFrame(ads.Ads.copy())
data.columns = ["y"]
for i in range(6, 25):
data["lag_{}".format(i)] = data.y.shift(i)
from sklearn.linear_model importLinearRegression
from sklearn.model_selection import cross_val_score
# 5折交叉驗(yàn)證
tscv = TimeSeriesSplit(n_splits=5)
def timeseries_train_test_split(X, y, test_size):
test_index = int(len(X)*(1-test_size))
X_train = X.iloc[:test_index]
y_train = y.iloc[:test_index]
X_test = X.iloc[test_index:]
y_test = y.iloc[test_index:]
return X_train, X_test, y_train, y_test
def plotModelResults(model, X_train=X_train, X_test=X_test, plot_intervals=False, plot_anomalies=False):
prediction = model.predict(X_test)
plt.figure(figsize=(15, 7))
plt.plot(prediction, "g", label="prediction", linewidth=2.0)
plt.plot(y_test.values, label="actual", linewidth=2.0)
if plot_intervals:
cv = cross_val_score(model, X_train, y_train,
cv=tscv,
scoring="neg_mean_absolute_error")
mae = cv.mean() * (-1)
deviation = cv.std()
scale = 1.96
lower = prediction - (mae + scale * deviation)
upper = prediction + (mae + scale * deviation)
plt.plot(lower, "r--", label="upper bond / lower bond", alpha=0.5)
plt.plot(upper, "r--", alpha=0.5)
if plot_anomalies:
anomalies = np.array([np.NaN]*len(y_test))
anomalies[y_test
anomalies[y_test>upper] = y_test[y_test>upper]
plt.plot(anomalies, "o", markersize=10, label = "Anomalies")
error = mean_absolute_percentage_error(prediction, y_test)
plt.title("Mean absolute percentage error {0:.2f}%".format(error))
plt.legend(loc="best")
plt.tight_layout()
plt.grid(True);
def plotCoefficients(model):
"""
繪制模型排序后的系數(shù)
"""
coefs = pd.DataFrame(model.coef_, X_train.columns)
coefs.columns = ["coef"]
coefs["abs"] = coefs.coef.apply(np.abs)
coefs = coefs.sort_values(by="abs", ascending=False).drop(["abs"], axis=1)
plt.figure(figsize=(15, 7))
coefs.coef.plot(kind='bar')
plt.grid(True, axis='y')
plt.hlines(y=0, xmin=0, xmax=len(coefs), linestyles='dashed');
y = data.dropna().y
X = data.dropna().drop(['y'], axis=1)
# 保留30%數(shù)據(jù)用于測(cè)試
X_train, X_test, y_train, y_test = timeseries_train_test_split(X, y, test_size=0.3)
# 機(jī)器學(xué)習(xí)
lr = LinearRegression()
lr.fit(X_train, y_train)
plotModelResults(lr, plot_intervals=True)
plotCoefficients(lr)
模型預(yù)測(cè)值:綠線為預(yù)測(cè)值,藍(lán)線為實(shí)際值
模型系數(shù)
好吧,簡(jiǎn)單的時(shí)差和線性回歸給出的預(yù)測(cè)質(zhì)量和SARIMA差得不遠(yuǎn)。有大量不必要的特征,不過(guò)我們將在之后進(jìn)行特征選擇。現(xiàn)在讓我們繼續(xù)增加特征!
我們將在數(shù)據(jù)集中加入小時(shí)、星期幾、是否周末三個(gè)特征。為此我們需要轉(zhuǎn)換當(dāng)前dataframe的索引為datetime格式,并從中提取hour和weekday。
data.index = data.index.to_datetime()
data["hour"] = data.index.hour
data["weekday"] = data.index.weekday
data['is_weekend'] = data.weekday.isin([5,6])*1
可視化所得特征:
plt.figure(figsize=(16, 5))
plt.title("Encoded features")
data.hour.plot()
data.weekday.plot()
data.is_weekend.plot()
plt.grid(True);
藍(lán)線:小時(shí);綠線:星期幾;紅色:是否周末
由于現(xiàn)有的變量尺度不同——時(shí)差的長(zhǎng)度數(shù)千,類別變量的尺度數(shù)十——將它們轉(zhuǎn)換為同一尺度再合理不過(guò),這樣也便于探索特征重要性,以及之后的正則化。
from sklearn.preprocessing importStandardScaler
scaler = StandardScaler()
y = data.dropna().y
X = data.dropna().drop(['y'], axis=1)
X_train, X_test, y_train, y_test = timeseries_train_test_split(X, y, test_size=0.3)
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)
lr = LinearRegression()
lr.fit(X_train_scaled, y_train)
plotModelResults(lr, X_train=X_train_scaled, X_test=X_test_scaled, plot_intervals=True)
plotCoefficients(lr)
測(cè)試誤差略有下降。從上面的系數(shù)圖像我們可以得出結(jié)論,weekday和is_weekend是非常有用的特征。
目標(biāo)編碼
我想介紹另一種類別變量編碼的變體——基于均值。如果不想讓成噸的獨(dú)熱編碼使模型暴漲,同時(shí)導(dǎo)致距離信息損失,同時(shí)又因?yàn)椤?點(diǎn) < 23點(diǎn)”之類的沖突無(wú)法使用實(shí)數(shù)值,那么我們可以用相對(duì)易于解釋的值編碼變量。很自然的一個(gè)想法是使用均值編碼目標(biāo)變量。在我們的例子中,星期幾和一天的第幾小時(shí)可以通過(guò)那一天或那一小時(shí)瀏覽的廣告平均數(shù)編碼。非常重要的是,確保均值是在訓(xùn)練集上計(jì)算的(或者交叉驗(yàn)證當(dāng)前的折),避免模型偷窺未來(lái)。
def code_mean(data, cat_feature, real_feature):
"""
返回一個(gè)字典,鍵為cat_feature的類別,
值為real_feature的均值。
"""
return dict(data.groupby(cat_feature)[real_feature].mean())
讓我們看下小時(shí)平均:
average_hour = code_mean(data, 'hour', "y")
plt.figure(figsize=(7, 5))
plt.title("Hour averages")
pd.DataFrame.from_dict(average_hour, orient='index')[0].plot()
plt.grid(True);
最后,讓我們定義一個(gè)函數(shù)完成所有的轉(zhuǎn)換:
def prepareData(series, lag_start, lag_end, test_size, target_encoding=False):
data = pd.DataFrame(series.copy())
data.columns = ["y"]
for i in range(lag_start, lag_end):
data["lag_{}".format(i)] = data.y.shift(i)
data.index = data.index.to_datetime()
data["hour"] = data.index.hour
data["weekday"] = data.index.weekday
data['is_weekend'] = data.weekday.isin([5,6])*1
if target_encoding:
test_index = int(len(data.dropna())*(1-test_size))
data['weekday_average'] = list(map(
code_mean(data[:test_index], 'weekday', "y").get, data.weekday))
data["hour_average"] = list(map(
code_mean(data[:test_index], 'hour', "y").get, data.hour))
data.drop(["hour", "weekday"], axis=1, inplace=True)
y = data.dropna().y
X = data.dropna().drop(['y'], axis=1)
X_train, X_test, y_train, y_test =
timeseries_train_test_split(X, y, test_size=test_size)
return X_train, X_test, y_train, y_test
X_train, X_test, y_train, y_test =
prepareData(ads.Ads, lag_start=6, lag_end=25, test_size=0.3, target_encoding=True)
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)
lr = LinearRegression()
lr.fit(X_train_scaled, y_train)
plotModelResults(lr, X_train=X_train_scaled, X_test=X_test_scaled,
plot_intervals=True, plot_anomalies=True)
plotCoefficients(lr)
這里出現(xiàn)了過(guò)擬合!Hour_average變量在訓(xùn)練數(shù)據(jù)集上表現(xiàn)如此優(yōu)異,模型決定集中全力在這個(gè)變量上——這導(dǎo)致預(yù)測(cè)質(zhì)量下降。處理這一問(wèn)題有多種方法,比如,我們可以不在整個(gè)訓(xùn)練集上計(jì)算目標(biāo)編碼,而是在某個(gè)窗口上計(jì)算,從最后觀測(cè)到的窗口得到的編碼大概能夠更好地描述序列的當(dāng)前狀態(tài)。或者我們可以直接手工移除這一特征,反正我們已經(jīng)確定它只會(huì)帶來(lái)壞處。
X_train, X_test, y_train, y_test =
prepareData(ads.Ads, lag_start=6, lag_end=25, test_size=0.3, target_encoding=False)
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)
正則化和特征選取
正如我們已經(jīng)知道的那樣,并不是所有的特征都一樣健康,有些可能導(dǎo)致過(guò)擬合。除了手工檢查外我們還可以應(yīng)用正則化。最流行的兩個(gè)帶正則化的回歸模型是嶺(Ridge)回歸和Lasso回歸。它們都在損失函數(shù)上施加了某種限制。
在嶺回歸的情形下,限制是系數(shù)的平方和,乘以正則化系數(shù)。也就是說(shuō),特征系數(shù)越大,損失越大,因此優(yōu)化模型的同時(shí)將盡可能地保持系數(shù)在較低水平。
因?yàn)橄拗剖窍禂?shù)的平方和,所以這一正則化方法稱為L(zhǎng)2。它將導(dǎo)致更高的偏差和更低的方差,所以模型的概括性會(huì)更好(至少這是我們希望發(fā)生的)。
第二種模型Lasso回歸,在損失函數(shù)中加上的不是平方和,而是系數(shù)絕對(duì)值之和。因此在優(yōu)化過(guò)程中,不重要的特征的系數(shù)將變?yōu)榱悖訪asso回歸可以實(shí)現(xiàn)自動(dòng)特征選擇。這類正則化稱為L(zhǎng)1。
首先,確認(rèn)下我們有特征可以移除,也就是說(shuō),確實(shí)有高度相關(guān)的特征:
plt.figure(figsize=(10, 8))
sns.heatmap(X_train.corr());
比某些現(xiàn)代藝術(shù)要漂亮
from sklearn.linear_model importLassoCV, RidgeCV
ridge = RidgeCV(cv=tscv)
ridge.fit(X_train_scaled, y_train)
plotModelResults(ridge,
X_train=X_train_scaled,
X_test=X_test_scaled,
plot_intervals=True, plot_anomalies=True)
plotCoefficients(ridge)
我們可以很清楚地看到,隨著特征在模型中的重要性的降低,系數(shù)越來(lái)越接近零(不過(guò)從未達(dá)到零):
lasso = LassoCV(cv=tscv)
lasso.fit(X_train_scaled, y_train)
plotModelResults(lasso,
X_train=X_train_scaled,
X_test=X_test_scaled,
plot_intervals=True, plot_anomalies=True)
plotCoefficients(lasso)
Lasso回k看起來(lái)更保守一點(diǎn),沒(méi)有將第23時(shí)差作為最重要特征,同時(shí)完全移除了5項(xiàng)特征,這提升了預(yù)測(cè)質(zhì)量。
XGBoost
為什么不試試XGBoost?
from xgboost importXGBRegressor
xgb = XGBRegressor()
xgb.fit(X_train_scaled, y_train)
plotModelResults(xgb,
X_train=X_train_scaled,
X_test=X_test_scaled,
plot_intervals=True, plot_anomalies=True)
我們的贏家出現(xiàn)了!在我們目前為止嘗試過(guò)的模型中,XGBoost在測(cè)試集上的誤差是最小的。
不過(guò)這一勝利帶有欺騙性,剛到手時(shí)序數(shù)據(jù),馬上嘗試XGBoost也許不是什么明智的選擇。一般而言,和線性模型相比,基于樹(shù)的模型難以應(yīng)付數(shù)據(jù)中的趨勢(shì),所以你首先需要從序列中去除趨勢(shì),或者使用一些特殊技巧。理想情況下,平穩(wěn)化序列,接著使用XGBoost,例如,你可以使用一個(gè)線性模型單獨(dú)預(yù)測(cè)趨勢(shì),然后將其加入XGBoost的預(yù)測(cè)以得到最終預(yù)測(cè)。
結(jié)語(yǔ)
我們熟悉了不同的時(shí)序分析和預(yù)測(cè)方法。很不幸,或者,很幸運(yùn),解決這類問(wèn)題沒(méi)有銀彈。上世紀(jì)60年代研發(fā)的方法(有些甚至在19世紀(jì)就提出了)和LSTM、RNN(本文沒(méi)有介紹)一樣流行。這部分是因?yàn)闀r(shí)序預(yù)測(cè)任務(wù)和任何其他數(shù)據(jù)預(yù)測(cè)任務(wù)一樣,在許多方面都需要?jiǎng)?chuàng)造性和研究。盡管有眾多形式化的質(zhì)量測(cè)度和參數(shù)估計(jì)方法,我們常常需要為每個(gè)序列搜尋并嘗試一些不同的東西。最后,平衡質(zhì)量和成本很重要。之前提到的SARIMA模型是一個(gè)很好的例子,經(jīng)過(guò)調(diào)節(jié)之后,它常常能生成出色的結(jié)果,但這需要許多小時(shí)、許多復(fù)雜技巧來(lái)處理數(shù)據(jù),相反,10分鐘之內(nèi)就可以創(chuàng)建好的簡(jiǎn)單線性回歸模型卻能取得相當(dāng)?shù)慕Y(jié)果。
-
函數(shù)
+關(guān)注
關(guān)注
3文章
4369瀏覽量
64187 -
時(shí)序
+關(guān)注
關(guān)注
5文章
397瀏覽量
37782 -
python
+關(guān)注
關(guān)注
56文章
4825瀏覽量
86175
原文標(biāo)題:機(jī)器學(xué)習(xí)開(kāi)放課程:九、基于Python分析真實(shí)手游時(shí)序數(shù)據(jù)
文章出處:【微信號(hào):jqr_AI,微信公眾號(hào):論智】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
時(shí)序數(shù)據(jù)庫(kù)HiTSDB的深度解析!
多片段時(shí)序數(shù)據(jù)建模預(yù)測(cè)實(shí)踐資料分享
關(guān)于時(shí)序數(shù)據(jù)庫(kù)的內(nèi)容
什么是時(shí)序數(shù)據(jù)庫(kù)?
同步時(shí)序數(shù)字電路的分析
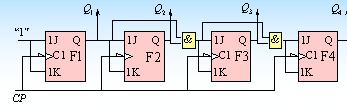
網(wǎng)絡(luò)流量時(shí)序數(shù)據(jù)可視分析
TableStore時(shí)序數(shù)據(jù)存儲(chǔ) - 架構(gòu)篇
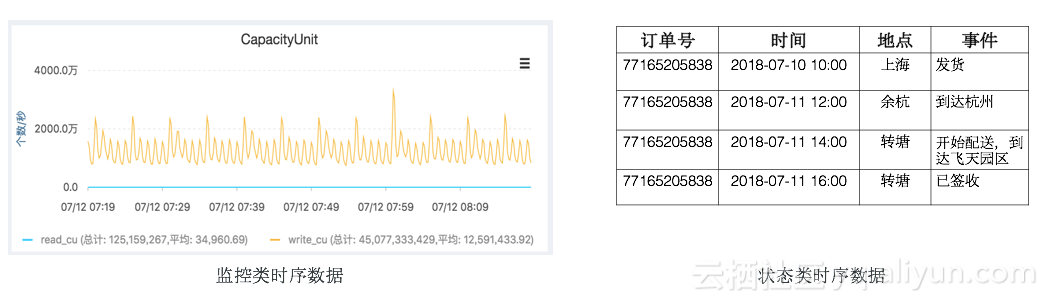
時(shí)序數(shù)據(jù)庫(kù)的前世今生
華為時(shí)序數(shù)據(jù)庫(kù)為智慧健康養(yǎng)老行業(yè)貢獻(xiàn)應(yīng)用之道
華為PB級(jí)時(shí)序數(shù)據(jù)庫(kù)Gauss DB,助力海量數(shù)據(jù)處理
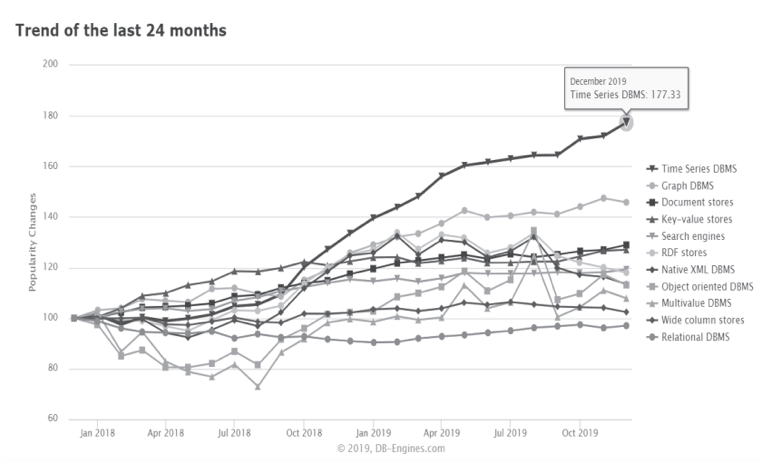
物聯(lián)網(wǎng)場(chǎng)景海量時(shí)序數(shù)據(jù)存儲(chǔ)與處理的關(guān)鍵技術(shù)
涂鴉推出NekoDB時(shí)序數(shù)據(jù)庫(kù),助力全球客戶實(shí)現(xiàn)低成本部署
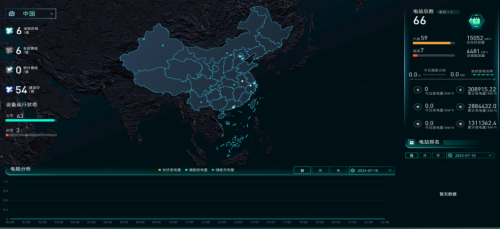
Tsmoothie:使用多種平滑技術(shù)平滑化時(shí)序數(shù)據(jù)
時(shí)序數(shù)據(jù)庫(kù)是什么?時(shí)序數(shù)據(jù)庫(kù)的特點(diǎn)
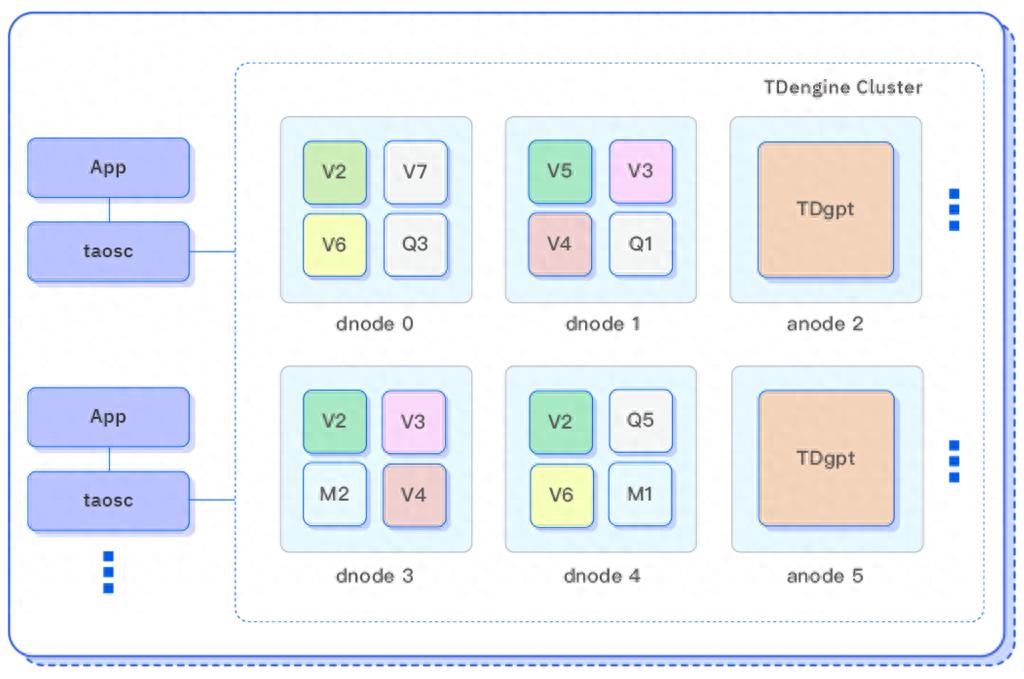
TDengine 發(fā)布時(shí)序數(shù)據(jù)分析 AI 智能體 TDgpt,核心代碼開(kāi)源





 分析和預(yù)測(cè)時(shí)序數(shù)據(jù)的主要方法,如何使用Python處理時(shí)序數(shù)據(jù)
分析和預(yù)測(cè)時(shí)序數(shù)據(jù)的主要方法,如何使用Python處理時(shí)序數(shù)據(jù)










評(píng)論