本文翻譯轉載于:Cadence Blog
作者:Gaurav
要點
●提出一種“代碼友好”的模型變體,以提高數值穩定性。
●實踐表明,如果使用隱式的、逐個方程分離的方法,該變體具有一定優勢。這個變體緩解了由壁面邊界條件引起的與 Durban 原始模型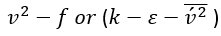 ?相關的“剛度問題”。
?相關的“剛度問題”。
●當雷諾數較高、近壁網格間距極小時,這種作用更加明顯。

挖掘 V2-f 湍流模型在復雜流動中的潛力
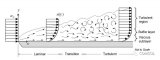
在高速空氣動力學中,利用二階矩閉合來研究沖擊/邊界層相互作用的研究很少。究其原因,是雷諾應力方程缺乏明確的二階擴散項,導致數值穩定性差。(例如,Batten 等,1997;Ha Minh 和 Vandromme,1986;Lien 和 Leschziner,1993)。當所有雷諾應力分量都存儲在精確位置時,這個問題會變得更加嚴重,導致速度與應力解耦和令人頭疼的棋盤振蕩。
在曲面上設置邊界條件較為復雜,這是在數值上實現二階矩閉合的一個重大挑戰。大多數低雷諾數 (Re)二階矩閉合模型都非常復雜,但只在較為簡單的流體場景下進行了驗證,例如 Craft 和 Launder(1996)開發的模型。因此,當 y+ 值約為 60 時,需要將高雷諾數模型(Gibson 和 Launder,1978)與標準低雷諾數渦流粘度模型結合起來,以確保湍流仿真中的平滑過渡。
然而,Patel(1985)等人研究的大多數低雷諾數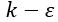 ?模型都在渦流-粘度表達式中加入了一個特殊的粘性阻尼函數?
?模型都在渦流-粘度表達式中加入了一個特殊的粘性阻尼函數?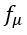 ,即?
,即?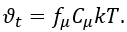 。
。
阻尼函數修正了渦流-粘度公式在接近固體壁面時不適當的漸近行為。它通常是非線性的,并能引起數值剛度。Durbin(1991)建議,在上述方程中,應使用與流線法向的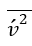 ?湍流應力,而不是使用 k 來表示壁面的運動阻塞。
?湍流應力,而不是使用 k 來表示壁面的運動阻塞。
因此,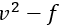 ?模型無需再使用粘性阻尼函數。
?模型無需再使用粘性阻尼函數。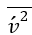 ?數量是從輸運方程推導而來,這是二階矩閉合理論的簡化版。
?數量是從輸運方程推導而來,這是二階矩閉合理論的簡化版。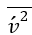 ?方程中的壓力-應變項發揮著至關重要的作用,可在壁面附近重新分配湍流能量,確保正確的湍流水平和恢復各向同性。這是通過輔助橢圓松弛方程實現的,該方程提供了更準確的近壁湍流行為表現。
?方程中的壓力-應變項發揮著至關重要的作用,可在壁面附近重新分配湍流能量,確保正確的湍流水平和恢復各向同性。這是通過輔助橢圓松弛方程實現的,該方程提供了更準確的近壁湍流行為表現。
理解 V2-f 湍流模型的核心原則
Durbin 1995 年的突破:針對精密流體分析,揭開原始 V2-f 模型的秘密。
Boussinesq 近似徹底改變了應力-應變關系,提高了準確度。
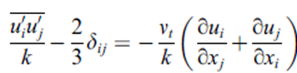
渦粘度由以下公式得出:
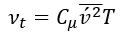
湍流時間由以下公式得出:
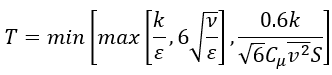
湍流長度尺度由以下公式得出:
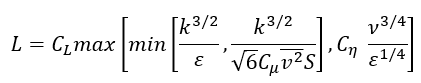
湍流時間和長度尺度由標準的 k-? 方程確定:
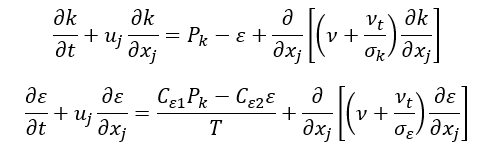
應變率大小定義為:
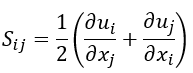
湍動能的產生定義為:
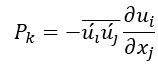
用 y 表示與墻體垂直的坐標,在無滑移邊界上,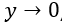 ,得出的結果是
,得出的結果是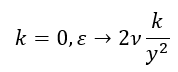
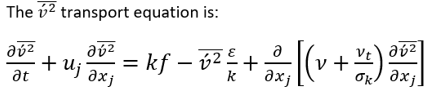
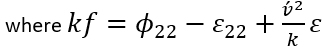
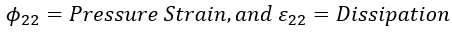
上述方程突出了湍流能量如何從流向分量中重新分配,通過函數 f 的橢圓松弛方程捕獲非局部效應。這種方法可確保精確、真實地描述流體中的空間相互作用,為復雜的湍流動力學提供了更深入的見解。
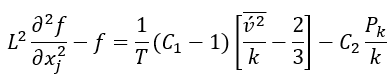
壁面附近的壓力-應變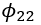 和耗散項?
和耗散項?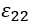 的漸近行為可描述為:
的漸近行為可描述為:
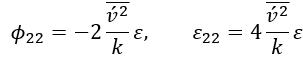
由此得出原始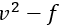 模型中
模型中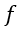 的邊界條件為:
的邊界條件為: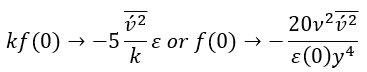
原始模型的系數如下:
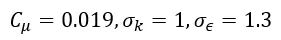
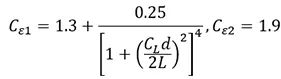
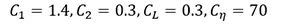
其中 d 是到壁面的距離。
橢圓松弛方法:湍流中的代碼友好創新(Lien 和 Durban,1996;Lien 等,1998)。
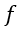 ?的邊界條件包含了一個?
?的邊界條件包含了一個?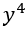 ?項的四次方,而?
?項的四次方,而?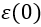 ?出現在分母上。這在層流和過渡區帶來了一個挑戰,
?出現在分母上。這在層流和過渡區帶來了一個挑戰,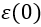 ?在此處的定義是不適定的,會引起數值振蕩。當采用分離數值過程時,這些振蕩變得更為明顯,因為它能防止
?在此處的定義是不適定的,會引起數值振蕩。當采用分離數值過程時,這些振蕩變得更為明顯,因為它能防止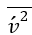 ?和?
?和?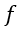 ?在壁面附近的隱式耦合。這啟發人們重新表述了
?在壁面附近的隱式耦合。這啟發人們重新表述了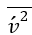 ?輸運方程中的項:
?輸運方程中的項:
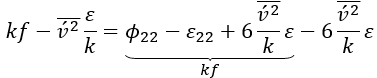
這里重新定義了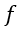 ,帶來橢圓松弛方程的修改,進而更好地捕捉流體動力學。
,帶來橢圓松弛方程的修改,進而更好地捕捉流體動力學。
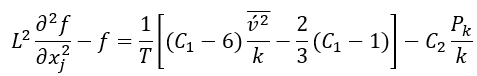
壁面的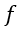 ?邊界條件導致?
?邊界條件導致?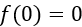 ?,這大大提高了數值穩定性。
?,這大大提高了數值穩定性。
注意,這些修改保留了與原始模型相同的漸近近壁行為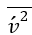 :
:
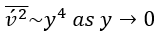
隨著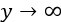 ?,由橢圓松弛引起的運動阻塞效應消失。
?,由橢圓松弛引起的運動阻塞效應消失。
得出的代碼友好型模型的常量表示為:
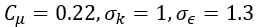
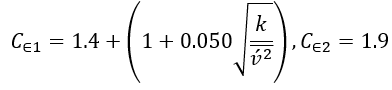
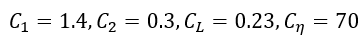
-
模型
+關注
關注
1文章
3486瀏覽量
49990 -
代碼
+關注
關注
30文章
4886瀏覽量
70253 -
湍流模型
+關注
關注
0文章
3瀏覽量
1692
原文標題:利用 V2-f 湍流模型進行更深入的流動研究
文章出處:【微信號:gh_fca7f1c2678a,微信公眾號:Cadence楷登】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
射流泵湍流場的數值模擬與實驗研究
Holon技術在敏捷制造系統中的應用研究
如何選擇以及有效使用不同的湍流模型





 V2-f湍流模型在復雜流動中的應用研究
V2-f湍流模型在復雜流動中的應用研究












評論