編者按：當你面對一個新概念時，你會怎么學習和實踐它？是耗費大量時間學習整個理論，掌握背后的算法、數學、假設、局限再親身實踐，還是從最簡單的基礎開始，通過具體項目解決一個個難題來提高你對它的整體把握？在這系列文章中，論智將采用第二種方法和讀者一起從頭理解機器學習。

“從零學習”系列第一篇從Python和R理解和編碼神經網絡來自Analytics Vidhya博主、印度資深數據科學開發人員SUNIL RAY。

本文將圍繞神經網絡構建的基礎知識展開，并集中討論網絡的應用方式，用Python和R語言實戰編碼。

目錄

神經網絡的基本工作原理

多層感知器及其基礎知識

神經網絡具體步驟詳解

神經網絡工作過程的可視化

如何用Numpy實現NN（Python）

如何用R語言實現NN

反向傳播算法的數學原理

神經網絡的基本工作原理

如果你是一名開發者，或曾參與過編程項目，你一定知道如何在代碼中找bug。通過改變輸入和環境，你可以用相應的各種輸出測試bug位置，因為輸出的改變其實是一個提示，它能告訴你應該去檢查哪個模塊，甚至是哪一行。一旦你找到正確的那個它，并反復調試，你總會得到理想的結果。

神經網絡其實也一樣。它通常需要幾個輸入，在經過多個隱藏層中神經元的處理后，它會在輸出層返回結果，這個過程就是神經網絡的“前向傳播”。

得到輸出后，接下來我們要做的就是用神經網絡的輸出和實際結果做對比。由于每一個神經元都可能增加最終輸出的誤差，所以我們要盡可能減少這個損耗（loss），使輸出更接近實際值。那該怎么減少loss呢？

在神經網絡中，一種常用的做法是降低那些容易導致更多loss的神經元的權重/權值。因為這個過程需要返回神經元并找出錯誤所在，所以它也被稱為“反向傳播”。

為了在減少誤差的同時進行更少量的迭代，神經網絡也會使用一種名為“梯度下降”（Gradient Descent）的算法。這是一種基礎的優化算法，能幫助開發者快速高效地完成各種任務。

雖然這樣的表述太過簡單粗淺，但其實這就是神經網絡的基本工作原理。簡單的理解有助于你用簡單的方式去做一些基礎實現。

多層感知器及其基礎知識

就像原子理論中物質是由一個個離散單元原子所構成的那樣，神經網絡的最基本單位是感知器（Perceptron）。那么，感知器是什么？

對于這個問題，我們可以這么理解：感知器就是一種接收多個輸入并產生一個輸出的東西。如下圖所示：

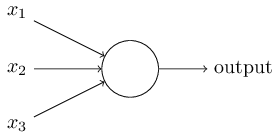
感知器

示例中的它有3個輸入，卻只有一個輸出，由此我們產生的下一個合乎邏輯的問題就是輸入和輸出之間的對應關系是什么。讓我們先從一些基本方法入手，再慢慢上升到更復雜的方法。

以下是我列舉的3種創建輸入輸出對應關系的方法：

直接組合輸入并根據閾值計算輸出。例如，我們設x1=0，x2=1，x3=1，閾值為0。如果x1+x2+x3>0，則輸出1；反之，輸出0。可以看到，在這個情景下上圖的最終輸出是1。

接下來，讓我們為各輸入添加權值。例如，我們設x1、x2、x3三個輸入的權重分別為w1、w2、w3，其中w1=2，w2=3，w3=4。為了計算輸出，我們需要將輸入乘以它們各自的權值，即2x1+3x2+4x3，再和閾值比較。可以發現，x3對輸出的影響比x1、x2更大。

接下來，讓我們添加bias（偏置，有時也稱閾值，但和上文閾值有區別）。每個感知器都有一個bias，它其實也是一種加權方式，可以反映感知器的靈活性。bias在某種程度上相當于線性方程y=ax+b中的常數b，可以讓函數上下移動。如果b=0，那分類線就要經過原點（0，0），這樣神經網絡的fit范圍會非常受限。例如，如果一個感知器有兩個輸入，它就需要3個權值，兩個對應給輸入，一個給bias。在這個情景下，上圖輸入的線性形式就是w1x1+ w2x2+ w3x3+1×b。

但是，這樣做之后每一層的輸出還是上層輸入的線性變換，這就有點無聊。于是人們想到把感知器發展成一種現在稱之為神經元的東西，它能將非線性變換（激活函數）用于輸入和loss。

什么是激活函數（activation function）？

激活函數是把加權輸入（w1x1+ w2x2+ w3x3+1×b）的和作為自變量，然后讓神經元得出輸出值。

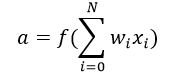
在上式中，我們將bias權值1表示為x0，將b表示為w0.

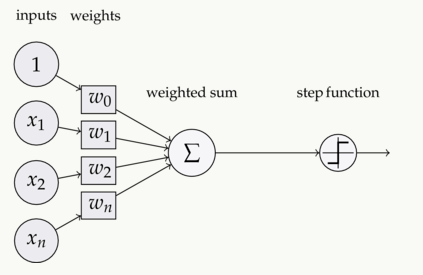
輸入—加權—求和—作為實參被激活函數計算—輸出

它主要用于進行非線性變換，使我們能擬合非線性假設、估計復雜函數，常用的函數有：Sigmoid、Tanh和ReLu。

前向傳播、反向傳播和Epoch

到目前為止，我們已經由輸入計算獲得了輸出，這個過程就是“前向傳播”（Forward Propagation）。但是，如果產出的估計值和實際值誤差太大怎么辦？其實，神經網絡的工作過程可以被看作是一個試錯的過程，我們能根據輸出值的錯誤更新之前的bias和權值，這個回溯的行為就是“反向傳播”（Back Propagation）。

反向傳播算法（BP算法）是一種通過權衡輸出層的loss或錯誤，將其傳回網絡來發生作用的算法。它的目的是重新調整各項權重來使每個神經元產生的loss最小化，而要實現這一點，我們要做的第一步就是基于最終輸出計算每個節點之的梯度（導數）。具體的數學過程我們會在最后一節“反向傳播算法的數學原理”中詳細探討。

而這個由前向傳播和反向傳播構成的一輪迭代就是我們常說的一個訓練迭代，也就是Epoch。

多層感知器

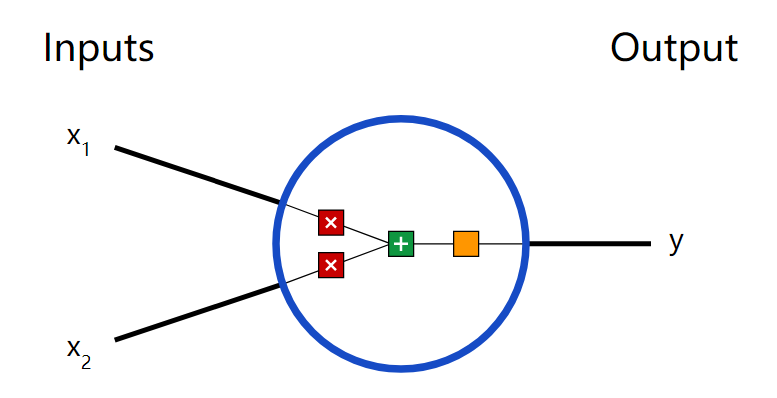
現在，讓我們繼續回到例子，把注意力放到多層感知器上。截至目前，我們看到的只有一個由3個輸入節點x1、x2、x3構成的單一輸入層，以及一個只包含單個神經元的輸出層。誠然，如果是解決線性問題，單層網絡確實能做到這一步，但如果要學習非線性函數，那我們就需要一個多層感知器（MLP），即在輸入層和輸出層之間插入一個隱藏層。如下圖所示：

圖片中的綠色部分表示隱藏層，雖然上圖只有一個，但事實上，這樣一個網絡可以包含多個隱藏層。同時，需要注意的一點是，MLP至少由三層節點組成，并且所有層都是完全連接的，即每一層中（除輸入層和輸出層）的每一個節點都要連接到前/后層中的每個節點。

理解了這一點，我們就能進入下一個主題，即神經網絡優化算法（誤差最小化）。在這里，我們主要介紹最簡單的梯度下降。

批量梯度下降和隨機梯度下降

梯度下降一般有三種形式：批量梯度下降法（Batch Gradient Descent）隨機梯度下降法（Stochastic Gradient Descent）和小批量梯度下降法（Mini-Batch Gradient Descent）。由于本文為入門向，我們就先來了解滿批量梯度下降法（Full BGD）和隨機梯度下降法（SGD）。

這兩種梯度下降形式使用的是同一種更新算法，它們通過更新MLP的權值來達到優化網絡的目的。不同的是，滿批量梯度下降法通過反復更新權值來使誤差降低，它的每一次更新都要用到所有訓練數據，這在數據量龐大時會耗費太多時間。而隨機梯度下降法則只抽取一個或多個樣本（非所有數據）來迭代更新一次，較之前者，它在耗時上有不小的優勢。

讓我們來舉個例子：假設現在我們有一個包含10個數據點的數據集，它有w1、w2兩個權值。

滿批量梯度下降法：你需要用10個數據點來計算權值w1的變化情況Δw1，以及權值w2的變化情況Δw2，之后再更新w1、w2。

隨機梯度下降法：用1個數據點計算權值w1的變化情況Δw1和權值w2的變化情況Δw2，更新w1、w2并將它們用于第二個數據點的計算。