疊加定理是電路分析中的一種基本方法,它允許我們通過將電路分解為簡單的子電路來求解復雜電路的響應。在某些情況下,我們可能希望將電源電壓設置為零,以便更簡單地分析電路。
一、疊加定理的基本原理
疊加定理是由德國物理學家海因里希·赫茲(Heinrich Hertz)于1887年提出的。它基于線性電路理論,即電路中的元件(如電阻、電容、電感等)滿足歐姆定律和基爾霍夫電壓定律。疊加定理的基本思想是,任何線性電路的響應(如電壓或電流)都可以表示為各個獨立電源單獨作用時響應的線性組合。
二、電源電壓為零的含義
在電路分析中,將電源電壓設置為零通常意味著我們希望忽略電源的影響,以便更專注于電路中其他元件的行為。這在某些情況下非常有用,例如在分析電路的靜態(tài)特性或在設計電路時考慮電源的替代方案。
三、實現(xiàn)電源電壓為零的方法
- 斷開電源 :最直接的方法是物理上斷開電源,但這在實際操作中可能不現(xiàn)實,特別是在需要電源供電的電路中。
- 使用理想電壓源 :在電路分析中,我們通常使用理想電壓源來代替實際電源。理想電壓源的特點是其內(nèi)阻為零,這意味著即使電源電壓為零,電路中的其他元件仍然可以正常工作。
- 使用短路 :在某些情況下,我們可以將電源的正負極短路,從而將電源電壓設置為零。這種方法在分析電路的某些特定特性時非常有用,例如在計算電路的短路電流時。
- 使用等效電源 :在某些情況下,我們可以通過引入等效電源來實現(xiàn)電源電壓為零。例如,如果我們有一個由多個電源組成的電路,我們可以通過引入一個等效電源來替代這些電源,從而簡化電路分析。
四、疊加定理在電源電壓為零時的應用
在電源電壓為零的情況下,疊加定理的應用需要我們重新考慮電路的響應。以下是一些具體的例子:
- 電阻電路 :在電阻電路中,電源電壓為零意味著電路中的電流為零。在這種情況下,我們可以使用疊加定理來分析電路中的電壓分布。例如,如果我們有一個由多個電阻組成的串聯(lián)電路,我們可以將每個電阻視為一個獨立的電源,然后使用疊加定理來計算每個電阻上的電壓。
- 電容電路 :在電容電路中,電源電壓為零意味著電路中的電荷為零。在這種情況下,我們可以使用疊加定理來分析電路中的電壓和電流。例如,如果我們有一個由多個電容組成的并聯(lián)電路,我們可以將每個電容視為一個獨立的電源,然后使用疊加定理來計算每個電容上的電壓和電流。
- 電感電路 :在電感電路中,電源電壓為零意味著電路中的電流為零。在這種情況下,我們可以使用疊加定理來分析電路中的電壓和電流。例如,如果我們有一個由多個電感組成的串聯(lián)電路,我們可以將每個電感視為一個獨立的電源,然后使用疊加定理來計算每個電感上的電壓和電流。
-
電流
+關注
關注
40文章
7136瀏覽量
134976 -
元件
+關注
關注
4文章
1195瀏覽量
37666 -
電源電壓
+關注
關注
3文章
1148瀏覽量
24758 -
疊加定理
+關注
關注
1文章
17瀏覽量
9170
發(fā)布評論請先 登錄
疊加定理的驗證
注意疊加定理使用的條件
疊加定理、替代定理的驗證
什么是疊加定理
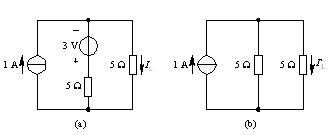





 如何在疊加定理中實現(xiàn)電源電壓為零
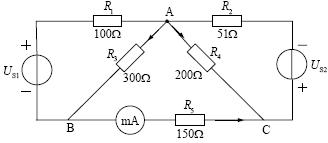
如何在疊加定理中實現(xiàn)電源電壓為零

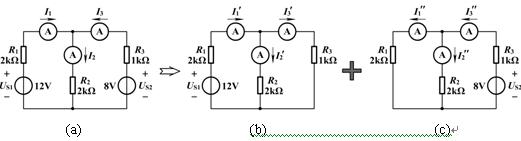










評論