1. 引言
有鑒于數(shù)字信號處理涉及的面太多,我們必須要把話題收縮。數(shù)字濾波的種類也是五花八門,因此再選一個(gè)小的類型,我們將圍繞離散線性時(shí)不變系統(tǒng)(Discrete Linear Time-Invariant System)來簡單討論一下陷波濾波器(Notch Filter)和梳狀濾波器(Comb Filter),通過代碼的演示和輸出,我們可以比較一下這兩類濾波器的特點(diǎn)。在本文中我們先以陷波濾波器為題來討論相關(guān)的內(nèi)容。
關(guān)于濾波,我們多少會(huì)了解一些,諸如帶通,帶阻,高通,低通等特性。信號濾波,其實(shí)我們在很多的應(yīng)用中都會(huì)不自覺地應(yīng)用起來,比如ADC值的多次采樣平均——這是一種典型的數(shù)字濾波方式,當(dāng)然也是最簡單濾波方式中的一種。
2. 關(guān)于線性移不變系統(tǒng)和數(shù)字濾波器
何謂線性移不變系統(tǒng)?主要是兩點(diǎn):
系統(tǒng)的弛豫狀態(tài)滿足可疊加原理(表現(xiàn)為線性,比例性)
系統(tǒng)的弛豫狀態(tài)時(shí)移不變,即任意時(shí)間平移量k,有x(n-k)→T→ y(n-k) )
再加上系統(tǒng)是因果的(如果一個(gè)系統(tǒng)的輸出僅僅依賴于過去和現(xiàn)在的輸入,而不依賴于未來的輸入,那么此系統(tǒng)就被稱為因果系統(tǒng)),穩(wěn)定的(系統(tǒng)輸出不是發(fā)散振蕩的),就構(gòu)成我們?yōu)V波器的幾個(gè)基本要素。
一個(gè)弛豫的系統(tǒng)是指當(dāng)初始時(shí)刻系統(tǒng)內(nèi)部無能量或所有狀態(tài)變量的初值為零的系統(tǒng),也就是說該系統(tǒng)的所有狀態(tài)變量都已經(jīng)"弛豫"到它們的穩(wěn)定或靜態(tài)值。在弛豫條件下,系統(tǒng)中不存在任何內(nèi)部能量或動(dòng)力以推動(dòng)系統(tǒng)產(chǎn)生輸出。換句話說,所有的輸出都將僅被輸入驅(qū)動(dòng)。
在差分方程或差分方程系統(tǒng)中,所謂的"初始條件為零"或"弛豫的初始條件",意味著所有的y(n)(對于n<0)都被假定為零,即系統(tǒng)在開始接收輸入(即n=0)之前是"靜止"或"弛豫"的。對于許多系統(tǒng)和信號處理分析,完全弛豫的假設(shè)能夠簡化計(jì)算和分析過程。然而,實(shí)際上,實(shí)際的物理系統(tǒng)可能需要一些時(shí)間才能達(dá)到完全弛豫的狀態(tài)。
離散數(shù)字濾波器在時(shí)域上可以用常系數(shù)差分方程來表示:
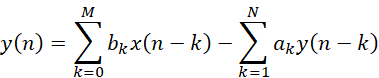
(1)
其中ak,bk都是已知常數(shù),但是該方程中,并不能直接看到y(tǒng)(n)和x(n)之間的等式關(guān)系,實(shí)際應(yīng)用最好通過軟件迭代的方式才方便處理。我們以參考書本[1]上的例子簡單說明。假如一個(gè)遞歸的輸入輸出方程有:
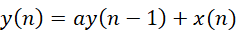
設(shè)定對n<0的輸入信號不計(jì),輸出部分只考慮y(-1),那么省掉遞推過程,可以得到:
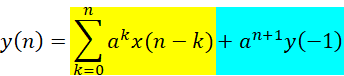
,其中n>0
y(n)的結(jié)果表達(dá)式中,第一部分是系統(tǒng)的零輸入響應(yīng),第二部分是零狀態(tài)響應(yīng)(顏色區(qū)分)。如果該系統(tǒng)的初始狀態(tài)是弛豫的,即有:
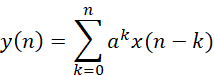
關(guān)于系統(tǒng)的線性,從上式可以知道,對于系統(tǒng)S和任意輸入x1,x2和常數(shù)c1,c2,有如下等式說明當(dāng)前系統(tǒng)是滿足疊加性的,因此系統(tǒng)是線性的。
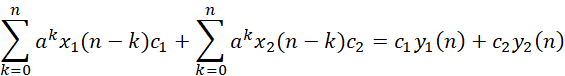
其中關(guān)于兩個(gè)響應(yīng)的說明:
零狀態(tài)響應(yīng)(ZSR):這是指當(dāng)系統(tǒng)的初始狀態(tài)為零,即沒有存儲的能量和信息,對系統(tǒng)的新輸入信號產(chǎn)生的響應(yīng)。這個(gè)響應(yīng)完全由當(dāng)前的輸入驅(qū)動(dòng),和系統(tǒng)在初始時(shí)刻的狀態(tài)無關(guān)。ZSR是系統(tǒng)特性(如系統(tǒng)函數(shù)、沖激響應(yīng)等)和輸入信號的函數(shù)。
零輸入響應(yīng)(ZIR):這是指當(dāng)系統(tǒng)的輸入為零,即沒有新輸入信號,系統(tǒng)由其初始狀態(tài)或初始條件產(chǎn)生的響應(yīng)。這通常描述了系統(tǒng)如何在沒有外部輸入的情況下,自然地演化和衰減,即系統(tǒng)的自由響應(yīng)。ZIR僅僅取決于系統(tǒng)的特性和初始狀態(tài)
上面的結(jié)論是通過簡單的時(shí)域例子來說明的,可能無法代表全狀態(tài)的方程。我們通過對式-1單邊Z變換的方式從復(fù)頻域的角度來加深理解一下(將Z=e^jω帶入,就轉(zhuǎn)入頻域)。單邊Z變換中,輸入信號x(n)被認(rèn)為是因果的,因此不考慮x(n),n<0的輸入,并且以前的輸入所有信號的作用都反映在初始條件y(-1),y(-2),…,y(-N)上。將式-1經(jīng)過單邊Z變換,我們可以得到[1]:
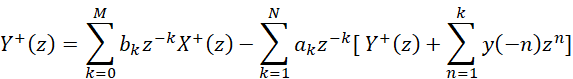
(2)
式-2經(jīng)過合并可得(式-3):

(3)
式-3中,前半部分就是系統(tǒng)的零狀態(tài)響應(yīng);后半部分就是零輸入響應(yīng),和系統(tǒng)以前的狀態(tài)相關(guān)。系統(tǒng)的響應(yīng)組成和在時(shí)域的響應(yīng)組成是相同的。而且我們也知道,復(fù)頻域中,下面的系統(tǒng)等式也是屬于LTI的:
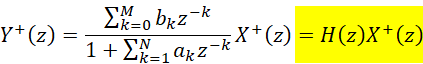
(4)
對于一般性的我們有:
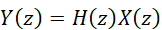
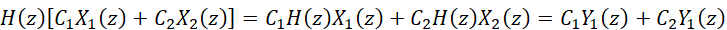 ????(5)
????(5)
式-5所表達(dá)的系統(tǒng)在復(fù)頻域的弛豫狀態(tài),是滿足疊加性要求的,因此系統(tǒng)是線性的。
我們再看關(guān)于系統(tǒng)符合線性系統(tǒng)的其他要求:
總響應(yīng)等于零輸入響應(yīng)和零狀態(tài)響應(yīng)之和;
零狀態(tài)響應(yīng)滿足疊加法則;
零輸入響應(yīng)滿足疊加法則。
關(guān)于系統(tǒng)時(shí)移,我們知道,在時(shí)域的時(shí)移,對應(yīng)復(fù)頻域中在z平面上的旋轉(zhuǎn):
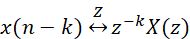
如果將z=e^jω代入,就可以將式-4轉(zhuǎn)換到頻域的輸入到輸出的頻幅響應(yīng)。我們有:
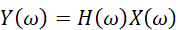
此時(shí)如果輸入信號有時(shí)移x(n-k),我們得到的系統(tǒng)響應(yīng)將是:
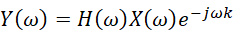
這種情況下,無論e^(-jωk)是系統(tǒng)的頻率響應(yīng)H(ω)引起的相應(yīng)變化,還是輸入信號X(ω)本身的時(shí)延引起的相位變化,效果是一樣的。另外,如果頻率響應(yīng)H(ω)對輸入信號的幅度有同樣的縮放功能|H(ω)|。這些對于信號本身可以不認(rèn)為是失真的。
事實(shí)上,線性時(shí)不變系統(tǒng)和濾波器這兩個(gè)術(shù)語是同義的。某種意義上,H(ω)對于輸入信號中不同的頻率成分起著加權(quán)函數(shù)或頻譜整形函數(shù)的作用[1]。這就是我們圍繞系統(tǒng)函數(shù)H(ω)展開如何設(shè)計(jì)濾波器的由來。
既然這里又回到了濾波器這個(gè)話題,我們再將內(nèi)容收縮一下,從陷波濾波器開始。式-1中,如果任意a_k=0,那么這個(gè)系統(tǒng)屬于有限沖激響應(yīng)系統(tǒng)(FIR);有任意a_k≠0,就會(huì)被稱之為無限沖擊響應(yīng)系統(tǒng)(IIR)。
3. 陷波濾波器(Notch Filter)
陷波濾波器,也稱為陷帶濾波器,是一種在某一特定頻率或者頻率范圍上,將信號的幅度衰減到極低甚至為零的濾波器。它屬于帶阻濾波器的特例,帶阻濾波器是一種抑制某一頻帶內(nèi)的信號而允許頻帶以外的信號通過的濾波器。它們的區(qū)別在于陷波濾波器的阻止帶寬通常更窄,目標(biāo)更準(zhǔn)確。如果是針對某個(gè)單一頻率的信號進(jìn)行濾波,那么該濾波器的品質(zhì)因數(shù)Q值的要求也會(huì)更高,以便讓被阻止的帶寬足夠窄而不影響該頻率附件信號的傳遞。但是過高的Q值就可能會(huì)引起濾波器的抖動(dòng),這個(gè)我們在設(shè)計(jì)濾波器的過程中,是需要留意的。
陷波濾波器的特性:
目標(biāo)頻率或頻道的信號被顯著削弱,而其他頻率的信號幾乎不受影響。
陷波頻率或頻帶的選擇往往能夠調(diào)整。
能有效削弱或消除特定頻率的噪聲或干擾。
應(yīng)用場合:
音頻處理:在音樂制作或音頻修復(fù)中,陷波濾波器用于消除特定的干擾音,例如電流電壓的噪聲。
工業(yè)現(xiàn)場信號采集處理系統(tǒng):比如用于濾除50或60Hz的工頻噪聲。
通信系統(tǒng):超窄帶陷波濾波器用于從廣帶信號中選擇性地濾除某一特定信號。
醫(yī)療和生物工程:用于消除生物和醫(yī)療信號中的電源頻率以及任何周期性干擾。
雷達(dá)和導(dǎo)航系統(tǒng):從信號中移除某一特定頻率的干擾。
陷波濾波器為了更準(zhǔn)確抑制特定頻段的信號而設(shè)計(jì),因此相比普通帶阻濾波器,它的阻帶通常會(huì)設(shè)置得更窄更精確。
我們通過模擬信號以及濾波處理后的信號之間進(jìn)行對比,來了解這種類型濾波器的特點(diǎn)。
模擬信號中有50Hz的工頻干擾信號需要濾除,保留20Hz的有用信號。先看結(jié)果,后查代碼[2](在本文的最后部分)。
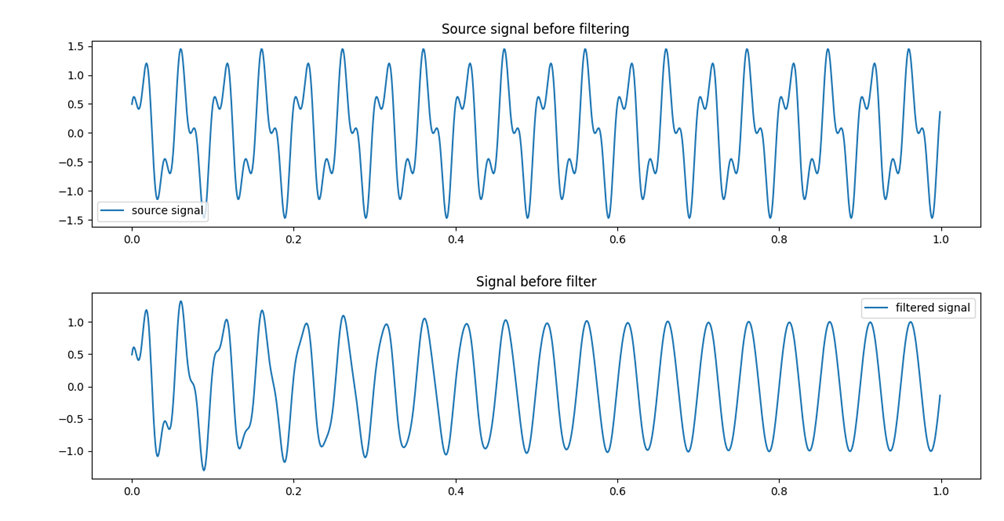
圖-1 信號濾波前后對比
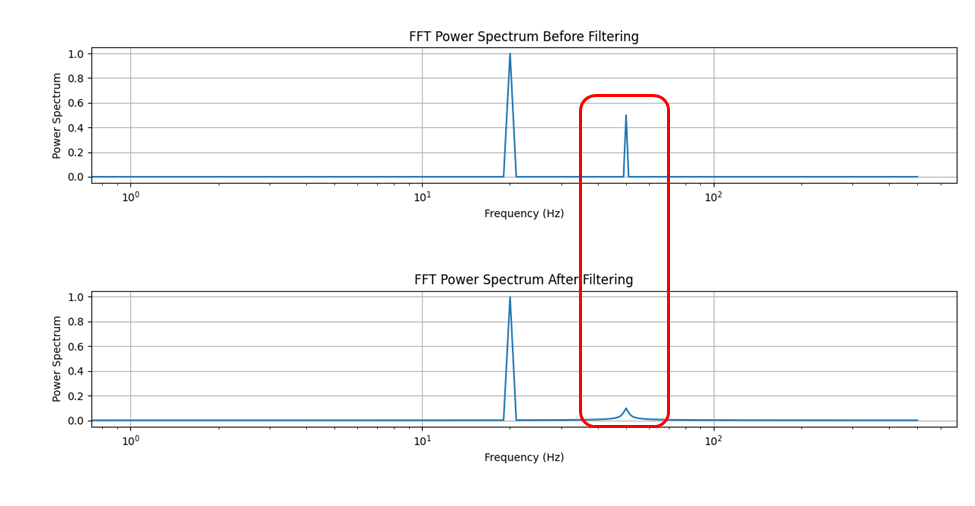
圖-2 信號濾波前后的頻譜圖(削弱后的50Hz信號)
第三個(gè)圖,是我們陷波濾波器典型的特征圖。在指定的頻率處對輸入信號進(jìn)行衰減,而其他頻率處保持通過。
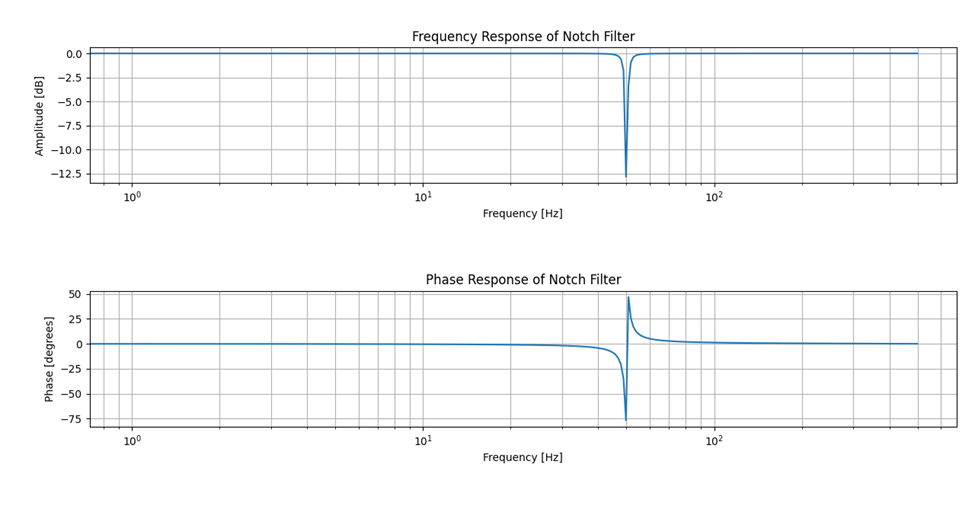
圖-3 濾波器的幅相頻響應(yīng)圖
該2階IIR濾波器在50Hz之外的頻域的信號都可以保持的通過性。參數(shù)如下(程序中有輸出):
b0~b2: [ 0.99479124, -1.89220538, 0.99479124]
a0~a2: [ 1.0 , -1.89220538, 0.98958248]
對應(yīng)的系統(tǒng)函數(shù)有:
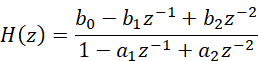
(6)
陷波濾波器對于特定的頻率過濾有其獨(dú)到的用途。該模擬測試程序可以在本文的附頁部分查看。通過計(jì)算得到系統(tǒng)函數(shù)在z平面中對應(yīng)的零點(diǎn)和極點(diǎn)結(jié)果如下(本文最后提供計(jì)算代碼):
| 零點(diǎn)1 | 零點(diǎn)2=零點(diǎn)1* | |
| 結(jié)果 | 0.9510565151337682+0.3090169979493239j | 0.9510565151337682-0.3090169979493239j |
| 絕對值 | 1.0 | 1.0 |
| 相角 | 18.00000021533598° | -18.00000021533598° |
| 極點(diǎn)1 | 極點(diǎn)2=極點(diǎn)1* | |
| 結(jié)果 | 0.94610269+0.3073632703736149j | 0.94610269-0.3073632703736149j |
| 絕對值 | 0.9947776032862823 | 0.9947776032862823 |
| 相角 | 17.997582759707843° | -17.997582759707843° |
在設(shè)計(jì)二階Notch濾波器時(shí),零點(diǎn)和極點(diǎn)的位置和數(shù)值對濾波器的性能起著關(guān)鍵的作用。在上面的模擬的濾波器中,z平面中的2個(gè)零點(diǎn)就在單位圓上,不過兩個(gè)極點(diǎn)已經(jīng)很靠近單位圓了,實(shí)際應(yīng)用中需要進(jìn)一步測試驗(yàn)證以避免濾波器的額外抖動(dòng)。
大家可以嘗試用C/C++的方式將參數(shù)轉(zhuǎn)換為代碼,成為你所需的濾波器。這里使用的是Python中的IIR方式,而如果真要用FIR方式實(shí)現(xiàn)同樣的效果,通常會(huì)需要很高的濾波器階次,反而會(huì)導(dǎo)致計(jì)算復(fù)雜度增加,響應(yīng)也會(huì)滯后。以下是設(shè)計(jì)陷波濾波器的一些基本的要求:
零點(diǎn)的位置:Notch濾波器的零點(diǎn)通常被放在單位圓上,其位置決定了阻止頻率的相關(guān)位置。要阻止的頻率就是零點(diǎn)所在的角度對應(yīng)的頻率。
極點(diǎn)的位置:極點(diǎn)的位置靠近零點(diǎn)可以產(chǎn)生較窄的Notch帶寬,這意味著濾波器能夠拒絕的頻率范圍較窄。相反,如果極點(diǎn)離零點(diǎn)較遠(yuǎn),那么Notch帶寬將較寬。但需要注意的是,極點(diǎn)的位置必須在單位圓內(nèi),否則濾波器將不穩(wěn)定。
零點(diǎn)和極點(diǎn)的數(shù)值:這些數(shù)值決定了濾波器的具體阻止頻率和帶寬。通過精確地選擇這些數(shù)值,可以設(shè)計(jì)出滿足各種應(yīng)用要求的濾波器。
總的來說,設(shè)計(jì)Notch濾波器時(shí),需要根據(jù)具體的阻止頻率和帶寬需求,精確地調(diào)整零點(diǎn)和極點(diǎn)的位置和數(shù)值。并且要確保極點(diǎn)的位置在單位圓內(nèi),以保證濾波器的穩(wěn)定。具體數(shù)值的確定可以借助各種濾波器設(shè)計(jì)工具進(jìn)行計(jì)算。
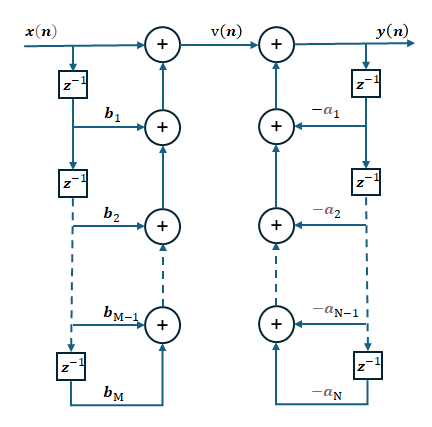
圖-4 濾波器的信號傳遞
4. 小結(jié)
在本文中,我們詳細(xì)探討了Notch濾波器的設(shè)計(jì)和應(yīng)用。我們理解了Notch濾波器的工作原理以及如何有效消除特定頻率的干擾。此外,我們還簡單了解了如何根據(jù)需求對濾波器進(jìn)行設(shè)計(jì),特別是零點(diǎn)和極點(diǎn)的定位。
通過理解和正確應(yīng)用這些原則,我們可以設(shè)計(jì)出性能優(yōu)秀的Notch濾波器,這對于許多應(yīng)用場景,如信號處理,噪聲消除等領(lǐng)域都是非常重要的。在很多工業(yè)現(xiàn)場的傳感器應(yīng)用中,會(huì)涉及很多信號的相對高速采集的場合,會(huì)用到Notch濾波器,尤其針對諸如工頻干擾,或者特定頻率的過濾等。
安費(fèi)諾傳感器(Amphenol Sensors)提供諸多滿足您應(yīng)用的可靠、準(zhǔn)確高精度的傳感器,但如果實(shí)際應(yīng)用過程中碰到一些異常的信號,可以和我們一起來分析原因,解決問題,根據(jù)實(shí)際工況來改善應(yīng)用。
后續(xù)的文檔中,我們將簡單討論另一種濾波器——梳狀濾波器(Comb Filter),并通過Python模擬該濾波器的功能和實(shí)現(xiàn),以及一些特情的處理方式。
陷波濾波器模擬測試Python代碼
import numpy as np import matplotlib.pyplot as plt from scipy import signal from scipy import fft,fftpack # 采樣頻率 fs = 1000 # 設(shè)計(jì)帶阻濾波器,過濾50Hz噪聲 f0 = 50.0 # Frequency to be removed from signal (Hz) Q = 30.0 # Quality factor w0 = f0/(fs/2) # 設(shè)計(jì)歸一化頻率 b, a = signal.iirnotch(w0, Q) # 生成一段帶噪音的信號 t = np.arange(0, 1.0, 1/fs) # Time vector x = np.sin(2*np.pi*20*t) # 20Hz sine wave x = x + 0.5*np.cos(2*np.pi*f0*t + .1) # 50Hz sine wave # 設(shè)計(jì)濾波器并應(yīng)用 yi = signal.lfilter(b, a, x) # 輸出該濾波器的參數(shù) print("Filter Parameters:","b:",b,"a:",a) # 繪制信號的波形圖 plt.figure(1) plt.subplot(211) plt.title('Source signal before filtering') plt.plot(t, x, label='source signal') plt.legend() # 繪制信號的頻譜圖 plt.subplot(212) plt.title('Signal before filter') plt.plot(t, yi, label='filtered signal') plt.legend() plt.tight_layout() plt.show() # 進(jìn)行FFT變換 xf = np.linspace(0.0, 1.0/(2.0/fs), fs//2) signal_original = fftpack.fft(x) # 源信號的FFT signal_filtered = fftpack.fft(yi) # 濾波之后的FFT # 繪制信號的FFT圖 plt.figure(figsize=(8, 4)) plt.subplot(2, 1, 1) plt.semilogx(xf, 2.0/len(x) * np.abs(signal_original[0:len(x)//2]), label='source signal') plt.title('FFT Power Spectrum Before Filtering') plt.xlabel('Frequency (Hz)') plt.ylabel('Power Spectrum') plt.grid() plt.subplot(2, 1, 2) plt.semilogx(xf, 2.0/len(signal_filtered) * np.abs(signal_filtered[0:len(signal_filtered)//2]), label='filtered signal') plt.title('FFT Power Spectrum After Filtering') plt.xlabel('Frequency (Hz)') plt.ylabel('Power Spectrum') plt.grid() plt.tight_layout() plt.show() # 繪濾波器的幅度頻響應(yīng)和相頻響應(yīng) freq, h = signal.freqz(b, a, fs=fs) plt.figure(figsize=(8, 4)) plt.subplot(2, 1, 1) plt.semilogx(freq, 20*np.log10(abs(h))) plt.title('Frequency Response of Notch Filter') plt.xlabel('Frequency [Hz]') plt.ylabel('Amplitude [dB]') plt.grid(which='both', axis='both') angle = np.unwrap(np.angle(h)) plt.subplot(2, 1, 2) plt.semilogx(freq, angle * 180 / np.pi) plt.title('Phase Response of Notch Filter') plt.xlabel('Frequency [Hz]') plt.ylabel('Phase [degrees]') plt.grid(which='both', axis='both') plt.tight_layout() plt.show()
通過濾波器的參數(shù)計(jì)算濾波器Z平面的零、極點(diǎn)(Zero/Pole)的Python
import cmath
import math
# 定義系數(shù)
b = [0.99479124, -1.89220538, 0.99479124] # 用新的參數(shù)替換掉表中的
a = [1.0, -1.89220538, 0.98958248]
# 計(jì)算0點(diǎn)
zero1 = (- b[1] + cmath.sqrt(b[1]**2 - 4 * b[0] * b[2])) / (2 * b[0])
zero2 = (- b[1] - cmath.sqrt(b[1]**2 - 4 * b[0] * b[2])) / (2 * b[0])
# 計(jì)算極點(diǎn)
pole1 = (- a[1] + cmath.sqrt(a[1]**2 - 4 * a[0] * a[2])) / (2 * a[0])
pole2 = (- a[1] - cmath.sqrt(a[1]**2 - 4 * a[0] * a[2])) / (2 * a[0])
# 計(jì)算相位角
zero1_abs = abs(zero1)
zero2_abs = abs(zero2)
pole1_abs = abs(pole1)
pole2_abs = abs(pole2)
zero1_angle = cmath.phase(zero1)
zero2_angle = cmath.phase(zero2)
pole1_angle = cmath.phase(pole1)
pole2_angle = cmath.phase(pole2)
phase_degrees_zero1 = math.degrees(zero1_angle)
phase_degrees_zero2 = math.degrees(zero2_angle)
phase_degrees_pole1 = math.degrees(pole1_angle)
phase_degrees_pole2 = math.degrees(pole2_angle)
print("Zeros: ", zero1, zero2)
print("Poles: ", pole1, pole2)
print("Zeros Angles: ", zero1_angle, zero2_angle, "abs Zeros:", zero1_abs, zero2_abs)
print("Poles Angles: ", pole1_angle, pole2_angle, "abs Poles:", pole1_abs, pole2_abs)
print("零點(diǎn)相位的度數(shù)為:", phase_degrees_zero1,phase_degrees_zero2)
print("極點(diǎn)相位的度數(shù)為:", phase_degrees_pole1,phase_degrees_pole2)
-
adc
+關(guān)注
關(guān)注
99文章
6635瀏覽量
548233 -
數(shù)字濾波器
+關(guān)注
關(guān)注
4文章
271瀏覽量
47501 -
陷波濾波器
+關(guān)注
關(guān)注
2文章
33瀏覽量
10240
原文標(biāo)題:數(shù)字濾波器(1)——陷波濾波器
文章出處:【微信號:安費(fèi)諾傳感器學(xué)堂,微信公眾號:安費(fèi)諾傳感器學(xué)堂】歡迎添加關(guān)注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
高通濾波器、低通濾波器、陷波器
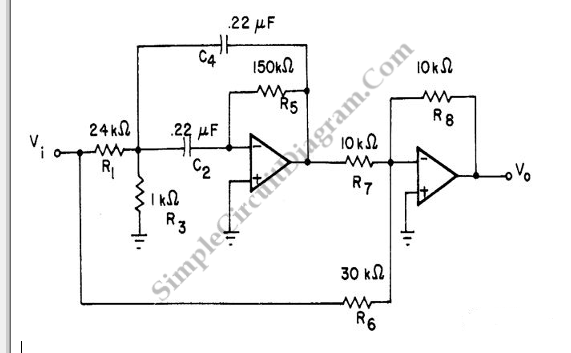
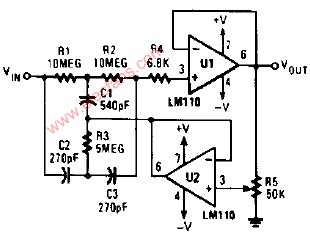
60Hz陷波濾波器電路圖





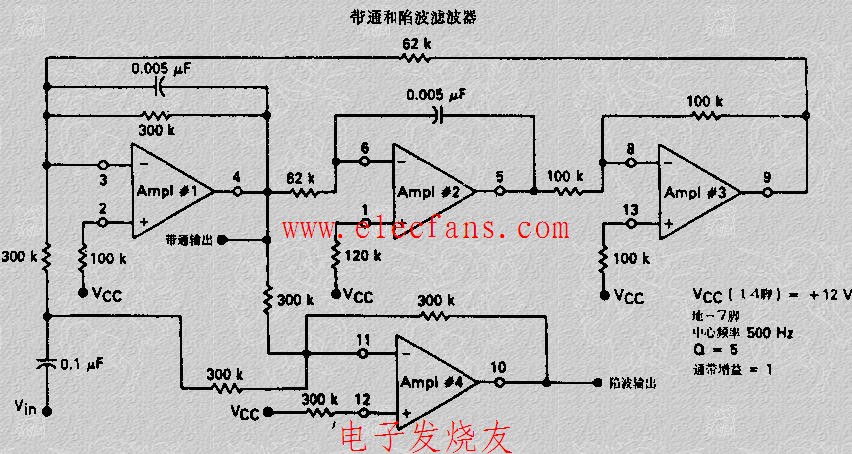
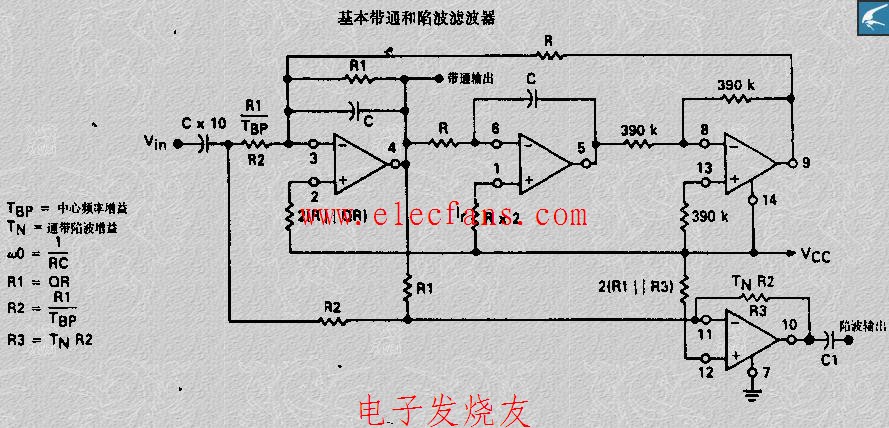
 陷波濾波器的相關(guān)知識
陷波濾波器的相關(guān)知識










評論