一、簡介
1、常見的浮點數(shù)表示方式是IEEE 754標(biāo)準(zhǔn),它規(guī)定了浮點數(shù)的存儲格式和運算規(guī)則,這個標(biāo)準(zhǔn)定義了兩種浮點數(shù)表示:單精度和雙精度。
2、任何一個浮點數(shù)的二進制數(shù)可以寫為:NUM = (-1) ^ S* 2 ^ E * M 。以float32類型舉例:
2.1、S表示符號:S為0時表示一個正數(shù);當(dāng)S為1時表示一個負數(shù)
2.2、E表示階乘、指數(shù):E是一個無符號整數(shù),所以E的取值范圍為(0~ 255)。但是在計數(shù)中指數(shù)是可以為負的,所以規(guī)定在存入E時,在它原本的值上加上中間數(shù)(127),在使用時減去中間數(shù)(127),這樣E的真正取值范圍就成了(-127~128)。對于E還分為以下三種情況:
(1)E不全為0,不全為1:這時就用正常的計算規(guī)則,E的真實值就是E的字面值減去127(中間值),M的值要加上最前面的省去的1
(2)E全為0:這時指數(shù)E等于1-127為真實值,M不再加上舍去的1,而是還原為0.xxxxxxxx小數(shù)。這樣為了表示0,和一些很小的整數(shù)。
(3)E全為1時分三種浮點數(shù)特殊情況:M全為0時,±無窮大(取決于符號位);M為非全0時,表示NaN。

2.3、M表示有效數(shù)字、尾數(shù):規(guī)定M的值一定是1 <= M < 2,可以寫成1.xxxxxxx的形式,所以規(guī)定M在存儲時舍去第一個1,只存儲小數(shù)點之后的數(shù)字。這樣做節(jié)省了空間,以float類型為例,就可以保存23位小數(shù)信息,加上舍去的1就可以用23位來表示24個有效的信息
3、單精度(32位):符號位(1 bit)、指數(shù)位(8 bits)、尾數(shù)位(23 bits)
4、雙精度(64位):符號位(1 bit)、指數(shù)位(11 bits)、尾數(shù)位(52 bits)
5、存儲格式:以float32的浮點數(shù)舉例如下圖

二、十轉(zhuǎn)二進制
1、以float32浮點數(shù)和23.375浮點數(shù)舉例
2、整數(shù)轉(zhuǎn)換方式:對2取余

3、小數(shù)轉(zhuǎn)換方式:對小數(shù)進行2乘留整再對小數(shù)2乘直至為小數(shù)部分為0

4、合并整數(shù)和小數(shù)部分:10111 和小數(shù)部分 0.011 得到二進制浮點數(shù) 10111.011
5、規(guī)范化和指數(shù)表示6、最終,將符號位、指數(shù)和尾數(shù)合并,得到IEEE 754標(biāo)準(zhǔn)的二進制浮點數(shù)表示為:

三、二轉(zhuǎn)十進制
1、以上面的23.375浮點數(shù)的轉(zhuǎn)換結(jié)果0 10000011 01110110000000000000000舉例
2、主要是這個公式:NUM = (-1) ^ S * 2 ^ E * M,分三步第一步:(-1) ^ S第二步:2 ^ E第三步:M3、符號位 (-1) ^ S:(-1)^04、指數(shù)位 2 ^ E :將二進制轉(zhuǎn)十進制為131,然后減去偏移值127,得到5、那么這里就是 2 ^ 46、M:分兩步
- 先轉(zhuǎn)換為二進制浮點數(shù),根據(jù)E不全為0或1的規(guī)則得到:1.01110110000000000000000
- 再用2的階乘的方式轉(zhuǎn)換為浮點數(shù),如下:
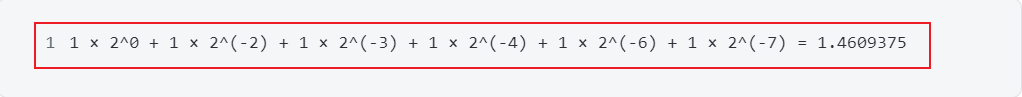
四、誤差
1、如下代碼展示

2、原因:在計算機中,由于浮點數(shù)的表示方式是有限的,有些十進制小數(shù)無法精確表示為二進制浮點數(shù)。這導(dǎo)致在進行浮點數(shù)運算時可能出現(xiàn)舍入誤差,進而導(dǎo)致預(yù)期的結(jié)果和實際的二進制浮點數(shù)表示的結(jié)果不完全相等。
3、將0.1轉(zhuǎn)為二進制

4、這個過程會一直持續(xù)下去,因為 0.1 在二進制中是一個無限循環(huán)小數(shù)。
5、將-0.1轉(zhuǎn)為二進制
6、首先,-0.1 可以表示為二進制的補碼形式。如果我們考慮一個32位的單精度浮點數(shù),其符號位為1,指數(shù)位為127(偏移值),尾數(shù)部分為 0.00011001100110011001100...(重復(fù)的 1100 模式)。
7、進行加法操作
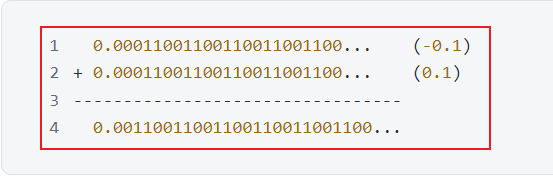
8、這個結(jié)果實際上是一個無限循環(huán)的二進制小數(shù)。由于計算機內(nèi)存是有限的,最終只能存儲一個有限位數(shù)的二進制小數(shù),因此可能會進行截斷或舍入操作,導(dǎo)致精度損失。
9、在實際計算機系統(tǒng)中,這種舍入誤差可能會導(dǎo)致結(jié)果不等于精確的零,因為我們不能精確地表示無限循環(huán)小數(shù)。這就是為什么在計算機編程中進行浮點數(shù)比較時,通常使用一個小的誤差范圍而不是直接比較相等。
10、改進方式
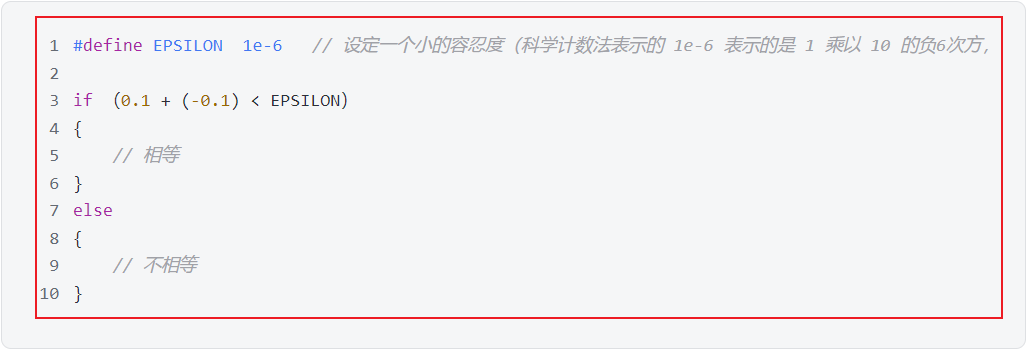
-
計算機
+關(guān)注
關(guān)注
19文章
7632瀏覽量
90225 -
編程
+關(guān)注
關(guān)注
88文章
3683瀏覽量
94885 -
計算機系統(tǒng)
+關(guān)注
關(guān)注
0文章
290瀏覽量
24531
發(fā)布評論請先 登錄
32位單精度IEEE-754浮點數(shù)轉(zhuǎn)換為10進制數(shù)
請問320F2812的浮點數(shù)算術(shù)標(biāo)準(zhǔn)是否遵循IEEE754 ?
幫助添加十進制浮點數(shù)
請問怎么將IEEE 754(32位十六進制)轉(zhuǎn)換為十進制浮點數(shù)?
IEEE754轉(zhuǎn)浮點數(shù)需要的數(shù)據(jù)類型轉(zhuǎn)換
浮點數(shù)的IEEE 754標(biāo)準(zhǔn)相關(guān)資料分享
ieee754標(biāo)準(zhǔn)下載
浮點數(shù)的表示方法

IEEE754浮點數(shù)格式
Cortex-M4 浮點數(shù)的存儲 和 FPU(Floating Point Unit) 雜記

談一談浮點數(shù)的精度問題

什么是浮點數(shù)
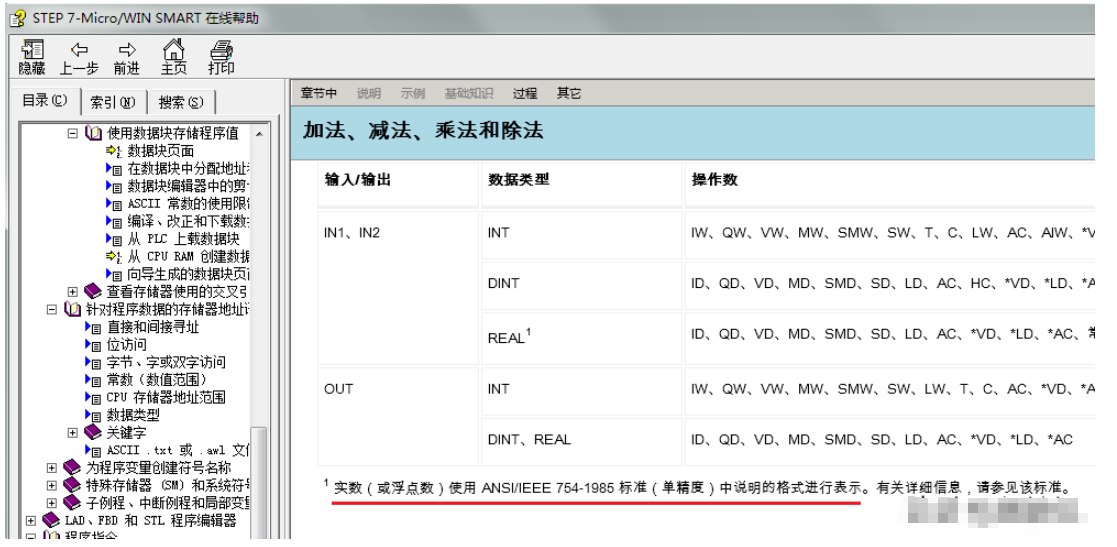
PLC中浮點數(shù)的二進制表示





 一文帶你秒懂IEEE 754浮點數(shù)
一文帶你秒懂IEEE 754浮點數(shù)











評論