時間序列分析是一種非常實用且強大的技術，用于研究隨時間變化的數據，例如銷售、交通、氣候等。異常檢測是識別偏離數據正常趨勢的值或事件的過程。在本文中，我將解釋什么是時間序列，它的組成部分是什么，它與其他類型的數據有何不同，如何檢測時間序列中的異常，以及進行此類檢測的最常見技術。

時間序列分析簡介

時間序列是在不同時點記錄一個或多個變量值的數據。例如，每天訪問網站的人數、每月城市的 average 溫度、每小時的股票價格等。時間序列非常重要，因為它們允許我們分析過去，理解現在，并預測未來。此外，時間序列幫助我們發現數據中的隱藏模式和趨勢，這些可以用于改進決策和策略。

然而，時間序列分析也帶來了挑戰，并且與非時間數據分析有所不同。主要區別之一是時間序列是時間依賴的，即數據的排序和范圍是相關且不能被忽視或更改的。另一個區別是時間序列通常是非平穩的，即它們的統計屬性（如均值和方差）會隨時間變化。這使得應用傳統的統計方法變得困難，這些方法假設數據的平穩性。

此外，時間序列分析需要對異常檢測采取不同的方法。異常是顯著偏離數據正常趨勢的值或事件。異常可能是由測量錯誤、結構變化、欺詐活動、特殊事件等引起的。異常檢測很重要，因為它可以提供隱藏在數據中的問題或機會的寶貴見解。然而，檢測時間序列中的異常比非時間數據更復雜，因為必須考慮到數據的時序依賴性、非平穩性和動態性質。

時間序列分析的基本概念

在我們詳細討論時間序列分析和異常檢測技術之前，我們需要定義什么是時間序列及其組成部分。時間序列是在不同時點測量的一個或多個變量值的序列。

時間序列有三個主要組成部分：日期、時間和特征。日期和時間指示了何時測量變量值。特征是我們希望分析的變量。在我們的示例中，日期是月份的一天，天氣是星期幾，特征是訪客數量。

為了能夠分析時間序列，我們需要滿足某些要求。第一個要求是有足夠的數據點，即隨時間變化的變量觀測值。所需的數據點數量取決于我們想要進行的分析類型以及數據收集的頻率。例如，如果我們想要分析數據的季節性，即數據作為時間的函數的周期性變化，我們需要至少一個完整的觀測周期，涵蓋所有可能的季節。如果數據每天收集一次，我們需要至少一年的數據才能分析年度季節性。

第二個要求是對數據的領域有深入的了解，即數據生成的背景和變量的含義。這有助于我們解釋分析結果并識別異常的可能原因。例如，如果我們分析網站的訪客數量，我們需要知道網站的類型、目標受眾、目標、影響流量的因素等。

第三個要求是對分析目標有清晰的定義，即我們想要從數據中發現什么以及我們想要如何使用它。分析的目標可能因用例和研究問題而異。例如，我們可能想要分析時間序列有：

描述數據隨時間的行為及其主要特征

基于過去的值預測未來的數據值

檢測數據中的異常及其原因

測試關于數據及其關系的假設

優化數據驅動的決策和行動

理解時間序列中的異常

在我們查看如何檢測時間序列中的異常之前，我們需要了解異常是什么以及它們如何在數據中表現出來。異常是顯著偏離數據正常趨勢的值或事件。異常可以分為兩種類型：點狀或集體。點狀異常是與時間序列中的其他值非常不同的孤立值。集體異常是與時間序列的其他部分不同的一組值。

例如，在下面的圖中，我們可以看到一個月內每天記錄網站訪客數量的時間序列。點狀異常用紅色標出，集體異常用藍色標出。

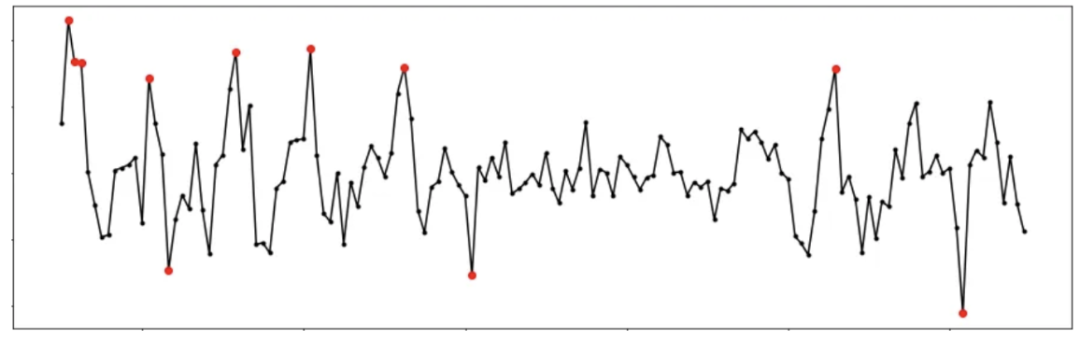
異常可能有不同的原因和含義。一些異常可能是由于測量、傳輸或數據處理錯誤引起的。這些異常通常被稱為噪聲，可以被忽略或糾正。其他異常可能是由于結構性變化、欺詐活動、特殊事件或其他影響數據的因素引起的。這些異常通常被稱為信號，檢測和分析它們可能很重要。

為了檢測時間序列中的異常，我們首先需要對數據隨時間的正常運動有所期望。這些期望是基于對時間序列的主要組成部分的分析，這些組成部分是：

趨勢，即數據長期變化的方向和速度。例如，上升趨勢表明數據隨時間增加，而下降趨勢表明數據隨時間減少。

季節性，即數據作為時間的函數的周期性變化。例如，年度季節性表明數據具有每年重復一次的循環模式，例如玩具店的銷售在12月增加而在1月減少。

周期性，即數據作為時間的函數的不規則變化。例如，經濟周期性表明數據具有依賴于外部因素（如GDP、通貨膨脹、失業率等）的波動趨勢。

噪聲，即數據作為時間的函數的隨機變化。例如，噪聲可能是由測量、傳輸或處理錯誤引起的。

在下面的圖中，我們可以看到一個具有上升趨勢、年度季節性和噪聲的時間序列示例。

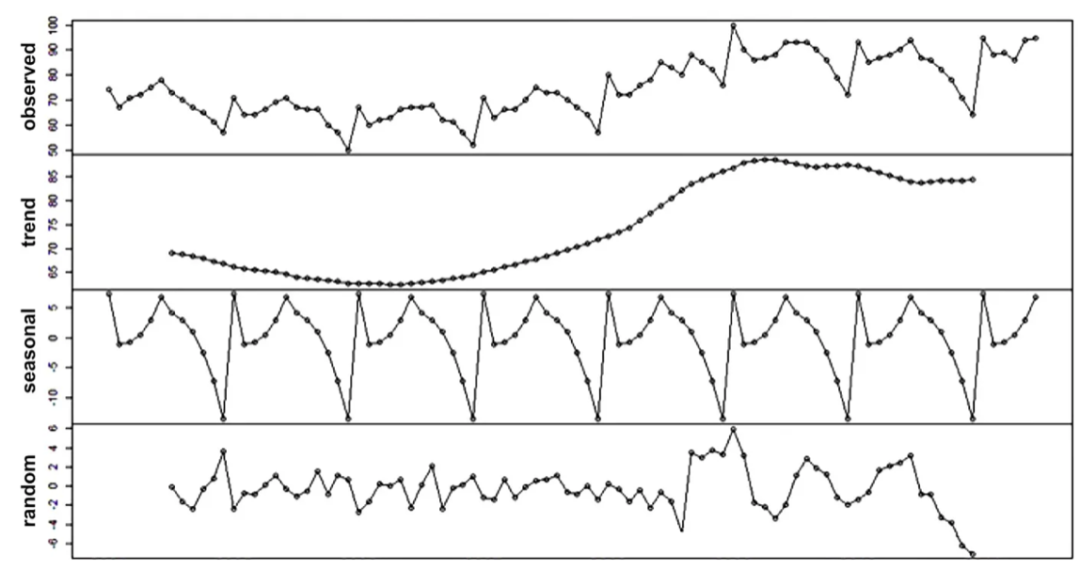
當分析時間序列時，我們需要考慮這些組件并了解它們如何隨時間變化。一個或多個組件的變化可能會引起異常。因此，通過理解和建模時間序列的趨勢、季節性、周期性和噪聲，我們可以建立對正常行為的期望，并相應地檢測偏離這些期望的異常。

時間序列分析的數據要求

如我們所見，為了能夠分析時間序列并檢測異常值，我們需要擁有滿足特定要求的數據。第一個要求是擁有足夠數量的數據點，即隨時間變化的變量觀測值。所需的數據點數量取決于我們想要進行的分析類型以及數據的收集頻率。例如，如果我們想要分析數據的趨勢，我們需要至少有十二個覆蓋相當長時間范圍的數據點。如果我們想要分析數據的季節性，我們需要至少有一個完整的觀測周期，涵蓋所有可能的季節。如果我們想要分析數據噪聲，我們需要至少有二十個足夠變化的數據點。

第二個要求是擁有捕捉時間變化的數據，即反映變量隨時間變化的變動。這意味著數據應該在規律且一致的時間間隔內收集，不跳過或重復某些觀測值。此外，數據必須是時間對齊的，即每個觀測值必須對應于變量被測量的時間。這暗示著數據必須轉換為適合時間序列分析的格式，例如日期時間格式。

第三個要求是擁有滿足時間序列主要組件（即趨勢、季節性和噪聲）分析的最低要求的數據。這些要求根據我們想要用于分析的模型而有所不同。例如，如果我們想要使用線性模型來分析趨勢，我們需要擁有在變量和時間之間具有線性關系的數據。如果我們想要使用指數模型來分析趨勢，我們需要擁有在變量和時間之間具有指數關系的數據。如果我們想要使用ARIMA模型來分析季節性和噪聲，我們需要擁有穩定或可微分的數據。

時間序列分析中的差分

如我們所見，時間序列分析中的一個主要挑戰是數據中存在非穩定性，即數據的統計屬性（如均值和方差）隨時間變化。這使得應用傳統的統計方法變得困難，因為這些方法假設數據是穩定的。為了使用這些方法，我們必須首先轉換數據，使其變得穩定，或至少近似穩定。進行這種轉換的最常見技術之一是差分。

差分包括從時間序列中的每個值中減去前一個值，從而得到一個代表數據隨時間變化的新的時序。例如，如果我們有一個時間序列 {x1, x2, x3, …}，它的一階差分是 {x2 - x1, x3 - x2, …}。差分可以重復多次，從而實現二階差分、三階差分等。差分的目的是從時間序列中移除趨勢和季節性成分，這些是非穩定性的主要原因。實際上，如果數據具有趨勢或季節性，其值將與前一個或后一個值相關。減去這些值可以減少或消除這種相關性。

例如，我們可以看到一個具有上升趨勢和年度季節性的時間序列。其一階差分去除了趨勢，但沒有去除季節性。其二階差分去除了趨勢和季節性。

差分是最廣泛使用的時間序列分析和異常檢測模型之一——ARIMA模型的基礎。

ARIMA模型介紹

ARIMA模型是時間序列分析和異常檢測中廣泛使用的模型之一。ARIMA代表自回歸差分移動平均模型（Autoregressive Integrated Moving Average）。這個模型結合了三個主要組成部分：

自回歸（AR）部分，它建模時間序列值與之前值之間的相關性。例如，如果數據是周期性的，時間序列值將受到過去值的影響。

差分（I）部分，它通過使時間序列差分來建模，使其變得穩定。例如，如果數據具有趨勢或季節性，差分將從時間序列中移除這些成分。

移動平均（MA）部分，它建模時間序列誤差與之前誤差之間的相關性。例如，如果數據有噪聲，時間序列誤差將受到過去誤差的影響。

ARIMA模型有三個主要參數：p、d和q。p參數表示模型中使用的自回歸項的數量。d參數表示為了使時間序列穩定而必須對時間序列進行差分的次數。q參數表示模型中使用的移動平均項的數量。例如，ARIMA(1,1,1)模型使用一個自回歸項、一個差分和一個移動平均項。

ARIMA模型可以用來描述、預測和檢測時間序列中的異常。為此，我們需要遵循幾個步驟：

首先，我們需要檢查時間序列是否穩定。我們可以使用統計測試，如增強的Dickey-Fuller測試，來檢查時間序列的均值和方差是否隨時間恒定。

其次，我們需要對時間序列進行差分，直到它變得穩定。我們可以使用圖表，如自相關函數圖和偏自相關函數圖，來確定所需的差分次數。

第三，我們需要使用優化方法，如最大似然法，來估計ARIMA模型的參數。我們可以使用模型選擇標準，如赤池信息準則或貝葉斯信息準則，來選擇p、d和q參數的最優值。

第四，我們需要使用驗證方法，如Ljung-Box測試或Jarque-Bera測試，來驗證ARIMA模型。我們可以使用圖表，如殘差圖或預測圖，來檢查模型是否與數據擬合良好，以及數據中是否存在任何異常。

第五，我們需要使用ARIMA模型來描述時間序列的主要特征，預測未來的時間序列值，并檢測時間序列中的異常。我們可以使用準確性度量，如均方誤差或平均絕對誤差，來評估預測和異常的質量。

時間序列異常檢測

在估計和驗證我們的時間序列的ARIMA模型后，我們可以使用它來檢測數據中的異常。異常是與數據的正常運行趨勢顯著偏離的值或事件。為了檢測異常，我們需要將觀察到的時間序列值與ARIMA模型預測的值進行比較。如果兩個值之間的差異大于某個閾值，我們可以將觀察到的值視為異常。

定義異常的閾值取決于多個因素，如置信水平、誤差分布、數據的頻繁程度等。通常，我們可以使用置信區間的概念來確定閾值。置信區間是一個以一定概率包含預測值的區間。例如，95%的置信區間意味著預測值在該范圍內的概率為95%。如果觀察到的值在置信區間之外，我們可以將其視為異常。

當我們在時間序列中檢測到異常時，我們還必須嘗試理解它們的原因和含義。一些異常可能是由于測量、傳輸或數據處理錯誤造成的。這些異常通常被稱為噪聲，可以被忽略或糾正。其他異常可能是由于結構性變化、欺詐活動、特殊事件或其他影響數據的因素造成的。這些異常通常被稱為信號，檢測和分析它們可能很重要。

為了理解異常的原因和含義，我們需要使用我們對數據領域的知識，即數據生成的背景和變量的含義。此外，我們需要使用其他信息來源，如其他相關時間序列、歷史數據、新聞、報告等。這有助于我們解釋異常檢測結果并確定可能采取的行動。

在本文中，我們已經看到了如何使用ARIMA模型進行時間序列分析和異常檢測。

結論

在本文中，我們已經看到了如何使用ARIMA模型進行時間序列分析和異常檢測。我們已經了解了什么是時間序列，它的組成部分是什么，它與其他類型的數據有何不同，如何在時間序列中檢測異常，以及進行這些操作的最常見技術。我們已經看到了如何驗證數據的平穩性，如何對時間序列進行差分，如何估計和驗證ARIMA模型，如何使用ARIMA模型來描述、預測和檢測時間序列中的異常，以及如何解釋異常檢測結果。

時間序列分析和異常檢測是研究隨時間變化的數據（如銷售、交通、氣候等）的非常有用的強大技術。這些技術允許我們分析過去，理解現在，并預測未來。此外，這些技術幫助我們發現數據中隱藏的模式和趨勢，這可以用來改進決策和策略。最后，這些技術幫助我們識別數據中的隱藏問題或機會，這可能是由數據中的異常引起的。

審核編輯：黃飛