今天我們要講的是應用于衛星通信領域的一個坐標轉換過程——機體坐標系與ENU坐標系的轉換。小D將以《機載衛星通信天線角度的計算推導》為基礎,來分析和推導坐標轉換公式。
開頭部分,我們先講一下ENU坐標系和機體坐標系的定義。
ENU坐標系(導航坐標系)
ENU坐標系中的E表示East,N表示North,U表示Up,翻譯過來就是東北天坐標系,小D第一次看到東北天這個名字時,還以為這個坐標系跟咱們祖國大東北有啥關系,后來發現沒有關系。
所以,為了不讓別人產生誤解,小D就叫的北天東,其他文獻中也有叫北東天的。另外還有一個坐標系是END,D表示Down。
ENU坐標系是以某個點為原點,三個軸表示出正東方向,正北方向和指向天上的方向,其中的“指向天上”是指垂直于水平面或海平面向上。
在大多數的文獻中,ENU坐標系Z軸一般表示指向天,如果X軸指向正東方向,Y軸指向正北方向,那么這個坐標系就是ENU右手坐標系;如果Z軸指向天,X軸指向正北,Y軸指向正東,那么這個ENU坐標系就是左手坐標系。
我們今天參考的文獻《機載衛星通信天線角度的計算推導》中的NEU坐標系是一個左手坐標系,并且ENU坐標系在這篇文獻中也被稱為導航坐標系,記作n系。ENU左手坐標系示意圖如下圖所示:
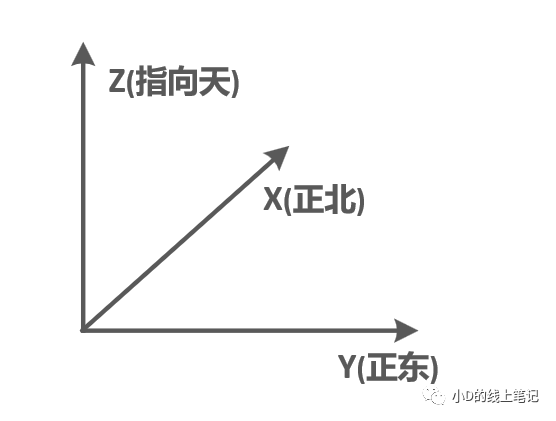
圖1ENU左手坐標系(導航坐標系n系)
機體坐標系(載體坐標系)
機體坐標系也叫載體坐標系,記作b系。機體坐標系也有很多種定義方式,有的地方定義的是左手坐標系,有的地方是右手坐標系;有的機體Z軸垂直于水平面向上,有的垂直于水平面向下。
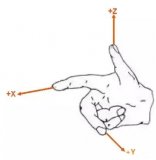
我們今天講的機體坐標系是這樣定義的:X軸正方向指向飛機前進的方向,與機身縱軸重合,Y軸指向機身右翼,Z軸垂直于機身平面向上,構成左手坐標系。
航向角、俯仰角、橫滾角
機體坐標系中有個重要的概念,就是機體姿態角,姿態角包含三個角度:航向角(yaw),俯仰角(pitch),橫滾角(roll),這三個角的定義如下:
航向角α:機頭方向在水平面的投影與正北之間的夾角,北偏東為正,范圍為0-360°;也可定義右偏為正,左偏為負,范圍為-180-180°。
俯仰角β:機頭方向與水平面的夾角,抬頭為正,范圍為-90-90°。
橫滾角γ:機體繞機體縱軸旋轉過的角度,右滾為正,范圍為-180-180°。
其實上面各個角度都是人為定義的,你也可以有不同的定義方式,重要的是在解算角度的時候,實際的偏離角度要和定義的角度一致。
機體坐標系的航向角、俯仰角和橫滾角示意圖如下所示:
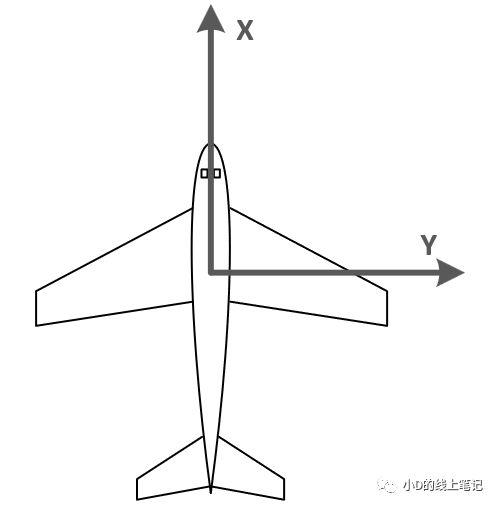
圖2 飛機水平飛行時的機體俯視圖
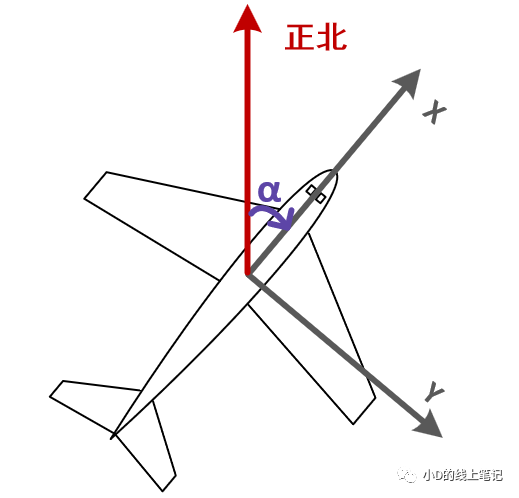
圖3 機體右偏時的航向角(俯視圖)
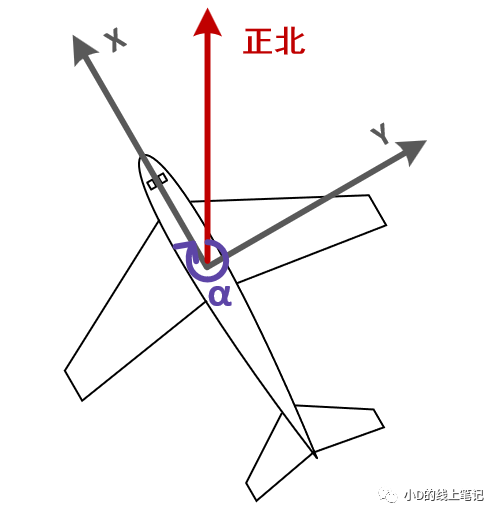
圖4機體左偏時的航向角(俯視圖)
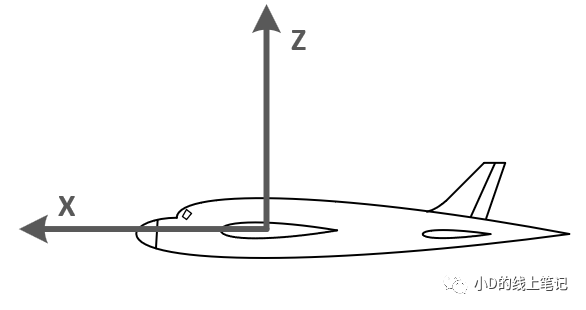
圖5飛機水平飛行時的機體左視圖
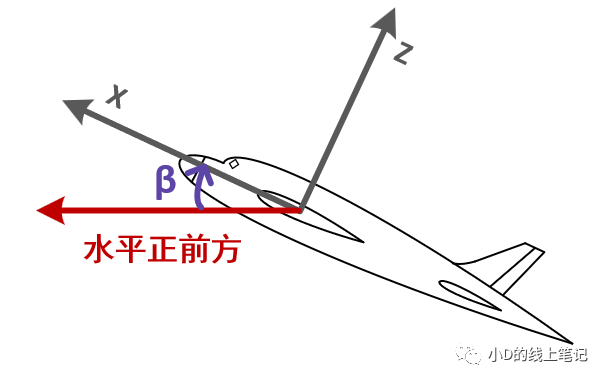
圖6 機體向上抬頭時的俯仰角(左視圖)
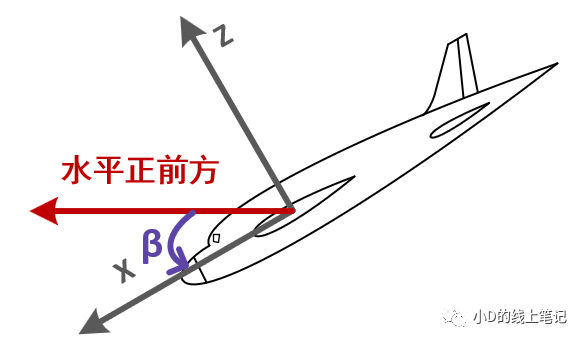
圖7機體向下低頭時的俯仰角(左視圖)
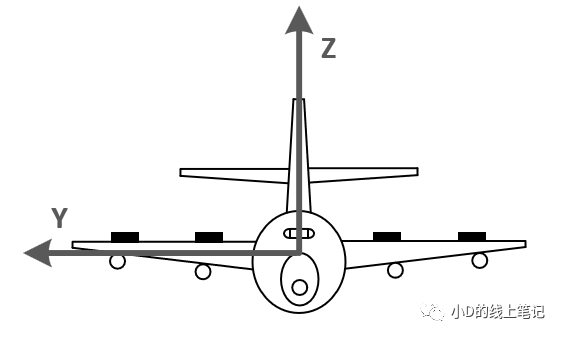
圖8 飛機水平飛行時的機體前視圖
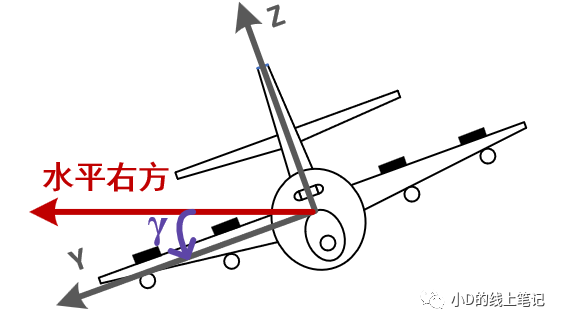
圖9 飛機向右滾轉時的橫滾角(前視圖)
注:向左滾轉和向右滾轉是以飛行員正視前方時的視角判斷的
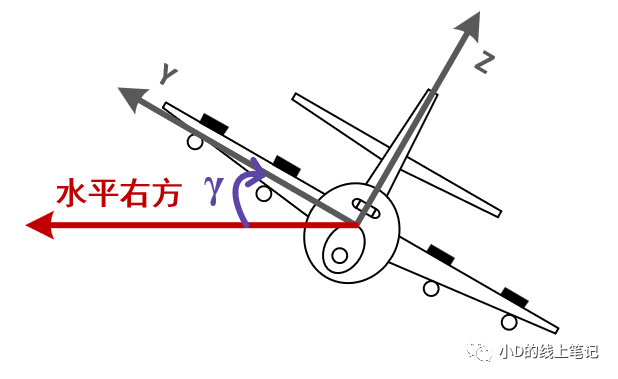
圖9飛機向左滾轉時的橫滾角(前視圖)
上面的圖是小D用visio畫的,應該可以很好地說明航向角、俯仰角和橫滾角。
ENU左手坐標系轉換到機體左手坐標系
ENU左手坐標系(導航坐標系)轉到機體左手坐標系(載體坐標系)是一個有點抽象的過程,小D第一次看這個轉換過程的時候,覺得頭都大了,想了好久才想明白是怎么旋轉的。為了講清楚轉換原理,小D根據《機載衛星通信天線角度的計算推導》里的圖,重新畫了一個三維圖,希望可以讓大家更好地理解這個過程。
下圖中,α是飛機的航向角,β是俯仰角,γ是橫滾角,大家可以結合小D參考的這篇文獻中的解釋來看這幾個角,小D把截圖放在文末了。
紫色的XnYnZn坐標系代表NEU坐標系,灰色的XbYbZb坐標系代表機體坐標系,虛線坐標系是中間過程坐標系。為了不讓示意圖看起來很復雜,文獻以及小D都把ENU坐標系XnYnZn的原點放到了機尾位置,它本來應該是和機體坐標系XbYbZb共用一個原點的。
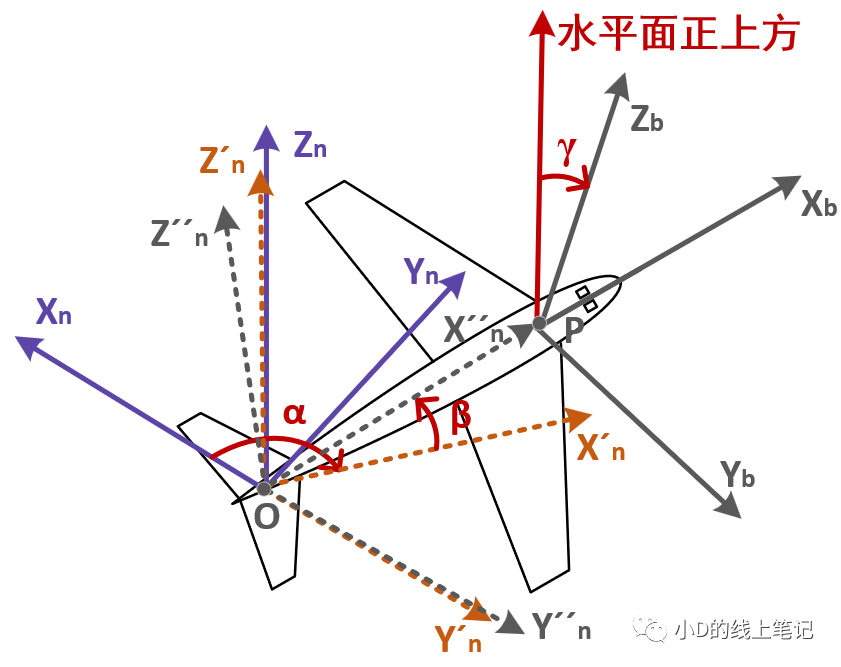
圖10 ENU坐標系轉換到機體坐標系的過程示意圖
現在我們來看看ENU坐標系XnYnZn轉換到機體坐標系XbYbZb的整個旋轉過程,一共有三個旋轉變換:
①XnYnZn坐標系先繞Zn軸順時針旋轉α角,形成X′nY′nZ′n坐標系;
②X′nY′nZ′n坐標系繞Y′n軸逆時針旋轉β角,形成X′′nY′′nZ′′n坐標系;
③X′′nY′′nZ′′n坐標系繞X′′n軸逆時針旋轉γ角,與機體坐標系XbYbZb重合。
圖中沒有畫出第③個過程,大家可以自己想像一下,或者用模型比劃一下,模型小D是用便簽紙和膠棒粘的一個三維的空間XYZ坐標系,用來理解空間中的變換過程,大家也可以像小D一樣做一個模型。

圖11 自制模型
由于上面的過程是左手坐標系的旋轉過程,所以順時針旋轉時,計算帶入的角度是正的,逆時針旋轉計算帶入的角度是負的,根據小D上次發的公眾號文章中的左手坐標系的旋轉矩陣,我們可以計算ENU坐標系XnYnZn轉換到機體坐標系XbYbZb的旋轉矩陣:
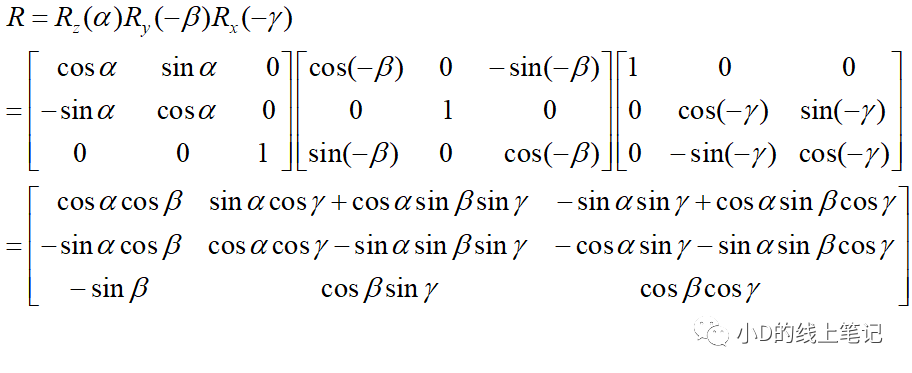
這就是最終的旋轉矩陣了。
機體左手坐標系轉換到ENU左手坐標系
機體坐標系轉到ENU坐標系的過程是一個逆過程:
①XbYbZb坐標系先繞Xb軸順時針旋轉γ角,形成X′bY′bZ′b坐標系;
②X′bY′bZ′b坐標系繞Y′b軸順時針旋轉β角,形成X′′bY′′bZ′′b坐標系;
③X′′bY′′bZ′′b坐標系繞Z′′b軸逆時針旋轉α角,與ENU坐標系XnYnZn重合。
所以,機體左手坐標系轉換到ENU左手坐標系旋轉矩陣為:
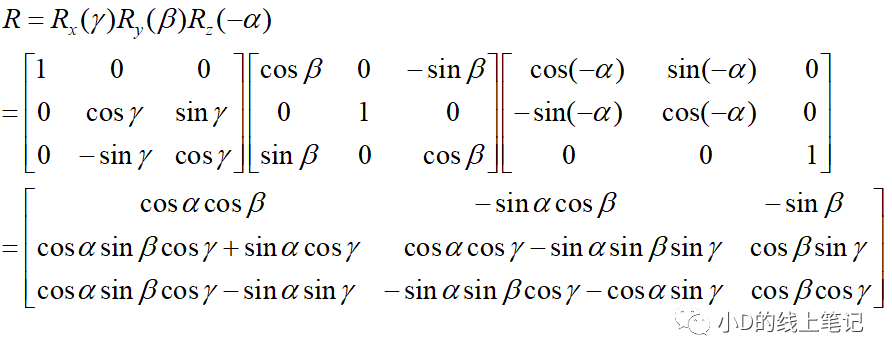
文獻中的公式推導
《機載衛星通信天線角度的計算推導》中的轉換過程示意圖如下圖所示,其中U軸是水平面正上方,小D繪制的跟文獻中的圖有一些不同的地方,就是Zb軸小D覺得應該畫在U軸的右邊。
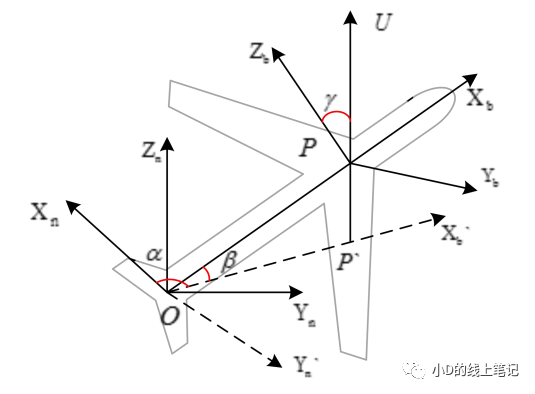
圖12文獻中的旋轉過程示意圖
除此之外,小D覺得文獻中給出的繞X,Y,Z軸逆時針旋轉的旋轉矩陣是有點問題的,正確的旋轉矩陣小D在上篇公眾號文章中給出了,大家可以對比一下,如果你覺得小D的觀點有問題,也可以告訴小D。

文獻中關于ENU坐標系(導航坐標系)與機體坐標系(載體坐標系)的推導過程是這樣的:

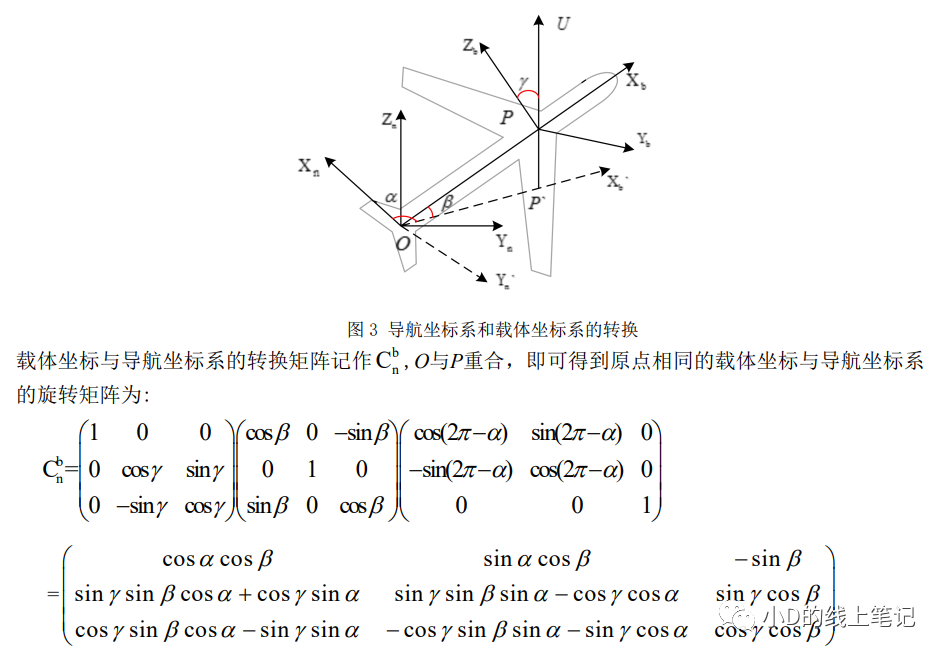
需要注意的是,上面的“逆時針旋轉2π-α”與“順時針旋轉α”是等效的。該篇文獻的作者講解的旋轉過程是導航坐標系轉到載體坐標系的過程,但是計算的旋轉矩陣是載體坐標系轉到導航坐標系的公式。
還有一點就是,作者可能是筆誤,三個矩陣相乘的結果也有一點問題,小D用matlab計算了一下作者給出的三個矩陣相乘的公式,計算過程如下:

圖13旋轉矩陣相乘的驗證代碼

圖14代碼計算結果
代碼計算結果如上圖所示,和作者計算的不一樣,字體有點小,大家可以自己在matlab里驗證旋轉矩陣計算結果。
審核編輯:劉清
-
matlab
+關注
關注
188文章
2997瀏覽量
233215 -
衛星通信
+關注
關注
12文章
749瀏覽量
39204
原文標題:機載衛星通信篇——ENU坐標系與機體坐標系的相互轉換
文章出處:【微信號:FPGA算法工程師,微信公眾號:FPGA算法工程師】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
如何計算才能把坐標系轉換成水平的坐標系?
機器人基坐標系標定方法研究
OPENGL坐標系介紹 世界坐標系和當前繪圖坐標系區別

帶你來剖析機器人的坐標系吧!
自動駕駛各個坐標系

三坐標如何建立坐標系?

深度剖析機器人的四大坐標系





 應用衛星通信領域的一個坐標轉換過程—機體坐標系與ENU坐標系的轉換
應用衛星通信領域的一個坐標轉換過程—機體坐標系與ENU坐標系的轉換
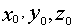











評論