上期講了繞組磁勢的齒諧波和相帶諧波產生的機理。本期繼續進一步分析繞組磁勢諧波的影響因素與諧波抑制。
1 關于相數與相帶諧波
上期講到,相帶諧波是由相帶劃分而引起的,由于相數有限,同一相帶內的槽內電流相位相同,磁勢變化斜率相同;不同相帶范圍內的槽內電流相位不同,磁勢變化斜率不同。使得整個繞組產生的磁勢由多段折線組成。用有限段折線逼近正弦曲線,必然會存在諧波,稱其為相帶諧波。定性地分析,如果相數增加,則折線段的數量將隨之增多,且每個相帶折線段的斜率也會按照正弦規律變化,這樣相數越多,折線的形狀就會越逼近基波正弦曲線,相帶諧波就越小。如果把相數增加到無窮大,則折線就變成了基波正弦曲線,此時就即不存在齒諧波也不存在相帶諧波了。由此可以定性地得出一個結論:相數越多,相帶諧波就越小。
深入分析表明,上述結論并不特別嚴謹。因為通常所說的電機相數是指繞組對外連接的電氣接口處電流具有的不同相位的數目。也就是說,按照這個定義,電機的相數就是電源(對電動機)或負載(對發電機)的相數。在這樣的定義下,并不一定是相數越多,相帶諧波就越小,因為電源相數不一定就是相帶數,或者說電源相數不一定就是繞組磁勢的折線段數,而繞組磁勢的相帶諧波大小主要取決于逼近正弦基波時的折線段數,即取決于相帶數,嚴格地說應該是逼近正弦基波所用的折線段數越多,相帶諧波越小。例如:通常所說的三相電機即可以劃分為120o相帶,這樣每對極就包括三個相帶,即每對極的磁勢由三段折線組成;也可以劃分為60o相帶,這樣每對極就包括六個相帶,即每對極的磁勢由六段折線組成。顯然六段折線比三段折線去逼近一個正弦曲線諧波會更小。如果三相繞組劃分為120o相帶,則其相帶諧波可能比兩相繞組的相帶諧波還要大,因為兩相繞組可以劃分為90o相帶。造成這種情況的原因主要是對于繞組相數概念的內涵與外延沒有很嚴格地加以限定所致。為此我們有必要重新對繞組的相數進行一個科學嚴謹的定義。
定義Ⅰ:從電機出線盒內看進去所通電流(或電壓)具有的不同相位的數目稱為電機繞組的物理相數。最常見的三相繞組通常就是指繞組的物理相數為三相。
定義Ⅱ:氣隙圓周的槽中電流所具有的不同相位的數目,稱為數學相數。例如,氣隙圓周的槽中有5種不同的電流相位,則稱繞組的數學相數為5相電機,同理,如果電流有50種不同的相位,則稱數學相數為50相電機!
按照上述定義,電機的物理相數雖然和數學相數存在著一定的關系,但二者也有著各自不同的含義。物理相數強調的是電機繞組對外電氣接口的電流(或電壓)所具有的不同相位的數目;而數學相數則強調的是繞組內部劃分出的相帶數。顯然對于單層繞組,數學相數就等于整個氣隙圓周上一個單元電機的相帶數。如前所述,繞組磁勢的相帶諧波大小和次數取決于折線段的段數,而折線段的段數又等于數學相數,由此應該進一步將上述的定性結論修正為:電機的數學相數越多,則磁勢的相帶諧波越小,波形越好。
但是,在分數槽的情況下,上面的定義仍然顯得不太嚴謹。例如:一個4極39槽的鼠籠轉子,按照上述定義,該轉子繞組的相數顯然為39相,而2極36槽的鼠籠轉子,相數為36,那么能不能說這個39相的轉子磁勢波形要好于36相轉子繞組的磁勢波形呢?如果畫出星形圖或者進行諧波分析,很快就會得出否定的結論!很顯然,上述39相轉子,其相鄰兩槽電流相位差為720o/39=18.46o電角度,而上述36相轉子,其相鄰兩槽電流相位差為360o/36=10o電角度。也就是說4極39相繞組的磁勢每個折線段覆蓋18.46o電角度;而2極36相繞組的磁勢每個折線段覆蓋10o電角度。也可以說4極39相繞組的磁勢是用39段折線逼近兩個正弦波;而2極36相繞組的磁勢是用36段折線逼近一個正弦波。這樣的話,顯然36相轉子磁勢波形反而要好于39相的轉子!這就是定義Ⅱ的局限性所在。為此,有必要對上述定義Ⅱ的數學相數再做進一步的限定。
定義Ⅲ:以一對極為基準,定義在氣隙圓周的一對極范圍內的槽中所具有的不同電流相位數目,稱為繞組的每對極的數學相數。由于每對極對應著一個基波波長,因此每對極的數學相數就是用來逼近一個周期正弦基波磁勢的折線段數。在這樣的定義下,就可以非常嚴謹地說,每對極的數學相數越多,相帶諧波就越小。
需要說明的是,按照上述定義Ⅱ,繞組的數學相數必定是一個正整數;而按照上述定義Ⅲ,每對極的數學相數不一定為正整數,例如上述4極39槽轉子的數學相數為39相,每對極的數學相數為19.5相;而2級36槽轉子的數學相數為36相,每對極的數學相數也是36相。事實上,在不同的文獻中,對異步電機轉子參數折算的過程中,確實既存在按定義Ⅱ的數學相數進行計算的,也存在按定義Ⅲ每對極的數學相數進行計算的,兩者得到的最終折算結果當然是一樣的!
2 物理相數和數學相數的關系
如前所述,物理相數是指電機出線盒內的電流相位數;而數學相數是指氣隙圓周的槽內所具有的不同電流相位數。二者有一定的關系,但二者并不一定相等。相同的數學相數可以對應不同的物理相數,反過來說,相同的物理相數也可以設計成不同的數學相數。換句話說,就是要實現某一數學相數,可以有不同的物理設計方法!
以單層繞組為例,由于每個線圈的兩個線圈邊電流方向相反,即兩個線圈邊內的電流相位差180o,而且對單層繞組來講,兩個線圈邊分別獨立地占有一個槽,因此任意一相繞組都必須劃分為兩個相等的相帶,一個為正相帶,另一個為負相帶。例如最簡單的單相電機,其物理相數為1,由于單相繞組的電流是一端流入,另一端流出,線圈的兩個有效邊電流相位相反,這樣的繞組在氣隙中分布時必然會使氣隙圓周上一部分槽中的電流和另一部分槽中的電流反相位,也就是說,氣隙圓周的槽中電流有兩種不同的相位,因此其數學相數為2相,即物理相數為1的繞組,數學相數為2。同理,物理相數為2的繞組,數學相數為4。
再來看看最常見的物理相數為3相的電機,其數學相數既可以是3,也可以是6,還可以是12!它們分別對應120o相帶接法,60o相帶接法,30o相帶接法(星/三角混合繞組)。由此可見,同樣的物理相數可以設計成不同的數學相數。而對于相帶諧波的大小,只取決于每對極的數學相數,二者是唯一的對應關系,而與物理相數卻并不是唯一的對應關系。當然從設計的靈活性角度來看,物理相數越多,可以設計的數學相數靈活度越大。要想減小相帶諧波,需要更多的數學相數,增多物理相數對增加數學相數總體來說是有利的。因此采用多相繞組有利于減小磁勢的相帶諧波。
但是相數太多物理上卻難以實現,例如要給39相的電機接入對稱的39相電源,顯然是難以實現的,供電的電力系統以及供電電纜會非常復雜,如果用半導體逆變來產生39相電源,顯然也會用到很多的半導體元器件,導致成本非常昂貴。因此,實際的電機要在這方面進行權衡折中,也就是盡量用最少的物理相數,實現盡可能多的數學相數,或者簡而言之,物理相數要少,而磁勢波形又要盡可能好!3相電機乃至于3相輸配電系統正是滿足這樣要求的折中產物!
3 關于齒槽數與齒諧波
說到齒諧波,自然會聯想到齒槽,于是就想當然地認為因定轉子開齒槽引起的諧波叫齒諧波。其實這種理解和說法存在一定的片面性,也非常不嚴謹。首先在概念上“齒諧波”本身不能成為一個孤立的概念,前面應該帶有一個定語,用來限定是哪個物理量的齒諧波,電勢的齒諧波?磁勢的齒諧波?氣隙磁場(或磁密)的齒諧波?氣隙磁導的齒諧波?等等;其次就是這樣定義齒諧波并沒有體現出各種物理量的齒諧波與齒槽之間的本質聯系。為此我們同樣有必要重新梳理一下有關齒諧波的一些概念。
定義Ⅳ:因定轉子開有齒槽導致氣隙磁導不均勻,進而使得氣隙磁導函數里面包含了一系列諧波,我們稱這種諧波為磁導齒諧波。
定義Ⅴ:因定轉子開有齒槽引起的氣隙磁場(磁密)的諧波稱為氣隙磁場(磁密)齒諧波。
定義Ⅵ:因電樞開有齒槽而引起的繞組磁勢諧波稱為槽諧波。也就是通常所說的磁勢齒諧波本文稱其為槽諧波,以示與其它齒諧波的區別。
定義Ⅶ:因電樞開有齒槽而引起的繞組電勢諧波稱為齒諧波。也就是通常所說的電勢齒諧波本文仍稱其為齒諧波。
經過以上梳理和重新定義,將原來籠統的“齒諧波”分成了四個內涵不同的概念,并賦予了每個概念完全不同且確切的含義。首先說磁導齒諧波,如果定轉子都不開槽且氣隙是均勻的,那么氣隙磁導就是一個常數,當定轉子開槽后,氣隙磁導就會因齒部和槽部的磁導率的巨大差別而產生一系列諧波,從這個角度看,磁導齒諧波與定轉子開槽有直接關系,磁導齒諧波是完全取決于電機結構的固有參數。其中因定子不旋轉,其開槽引起的磁導諧波只是一些靜止不動的空間諧波;而轉子是旋轉的,其開槽引起的磁導諧波會隨轉子的旋轉而一同旋轉,因此磁導諧波即是空間的函數又是時間的函數。再說氣隙磁密的齒諧波,它是磁勢在氣隙磁導上作用的結果,是磁勢與氣隙磁導調制的結果,即使磁勢是純正弦波,經過磁導齒諧波的調制也會使氣隙磁密產生一系列的諧波,因此氣隙磁密的齒諧波是定轉子開齒槽的間接作用產物,它不僅與電機結構有關,也與電機運行狀態有關,是一個狀態參數和中間過程參數。其實電機設計制造完成后,客戶并不關心氣隙磁密的波形如何,而是關心氣隙磁密反映在電機最終特性上造成的影響和結果。電勢的齒諧波,也就是定義Ⅶ所說的齒諧波,它是氣隙磁密在繞組中作用的結果,它與齒槽的關系更是間接的,齒槽對電勢齒諧波的影響不會增加齒諧波的次數,只會對主極磁勢中與齒槽數相關的某些特定次數起到放大的作用,也就是說定子不開槽時主極磁勢有什么次數的諧波,開槽后電勢中就會有什么次數的諧波,磁勢中沒有的諧波次數,開槽后電勢中也不會有該磁勢的諧波,即定子開槽不會增加或減少電勢諧波的次數,開槽只會對(k?Z1/p)±1次齒諧波有強烈的放大作用。由于電勢是時間的函數,因此電勢齒諧波也僅是時間的函數。關于電勢齒諧波,我們在電機繞組(8)和電機繞組(9)中進行過詳細的論述,這里不再贅述。本文主要討論的是磁勢齒諧波,也就是定義Ⅵ所說的槽諧波。磁勢是一種安匝數的概念,是線圈中的電流乘以匝數,它只與氣隙中的安導波分布有關,與氣隙磁導沒有任何關系,從這個角度講,磁勢與是否開槽沒有任何關系。但由于繞組的導體都是被嵌放在槽內的,而槽是離散而不是連續分布在氣隙圓周上,而且我們假設線圈的導體都是集中分布在槽口的中心線上,這樣就使得安導波不是一個連續的分布函數,而是集中在每個槽口中心線上的離散脈沖函數,由此導致磁勢波每經過一個槽口就會發生一次跳變(臺階),從而使磁勢中出現一系列的空間諧波,我們定義這種諧波為槽諧波。從這個角度講,似乎槽諧波又與齒槽有一定的關系,但設想如果定子不開槽,而線圈的導體仍然是離散地分布在氣隙圓周上,那么磁勢仍然會產生臺階,磁勢中也就仍然存在所謂的槽諧波,由此可見,槽諧波其實與是否開槽沒有必然的聯系,只是因為導體集中嵌放在槽內,導致安導波不連續而產生的諧波。
我們還是回到線圈導體嵌放在槽內,而且槽內導體集中分布在槽口中心線上這個假設上來,重點分析槽諧波與槽數的關系。
假設氣隙圓周(定子或轉子)上開有若干個槽,每個槽內的電流相位都不同,也就是說每個槽都是一相,槽數和數學相數相等,這樣在任意時刻每個槽內電流大小都是按正弦規律分布。其實前面舉例的4極39槽鼠籠轉子就屬于這種情況,每個槽內導體都是一相,因此我們就繼續以此為例,來分析槽諧波和槽數的關系。由于槽數是有限的,每個槽內電流相位都不同,因此任意時刻每個槽內電流大小都是按照正弦規律分布。這樣磁勢在每個槽口處就跳變一個臺階,臺階的高度按正弦規律變化。也就是說在槽數有限的條件下,這種方式產生的磁勢是最接近正弦波的,這種情況下僅存在槽諧波而不會存在相帶諧波。如圖1即為該鼠籠轉子在某一時刻的磁勢分布圖。其中臺階形曲線為實際的磁勢曲線,與理想正弦曲線相比可以明顯看到,每次跳變的高度是嚴格符合正弦規律。
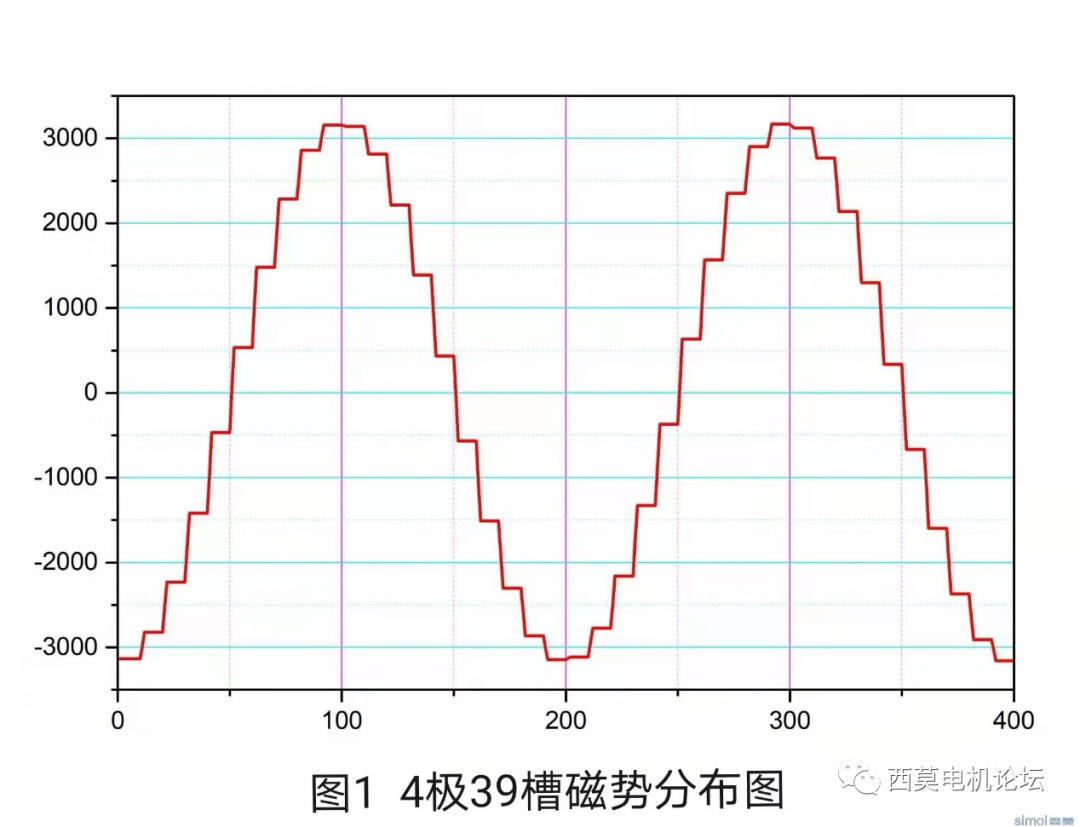 ? 由于這種情況下不存在相帶諧波,只存在槽諧波,進一步將圖1中的臺階波減去理想正弦基波便得到槽諧波的波形,如圖2 b)所示,為了看清槽諧波的形狀,單獨再把槽諧波進一步放大如圖3所示。
? 由于這種情況下不存在相帶諧波,只存在槽諧波,進一步將圖1中的臺階波減去理想正弦基波便得到槽諧波的波形,如圖2 b)所示,為了看清槽諧波的形狀,單獨再把槽諧波進一步放大如圖3所示。
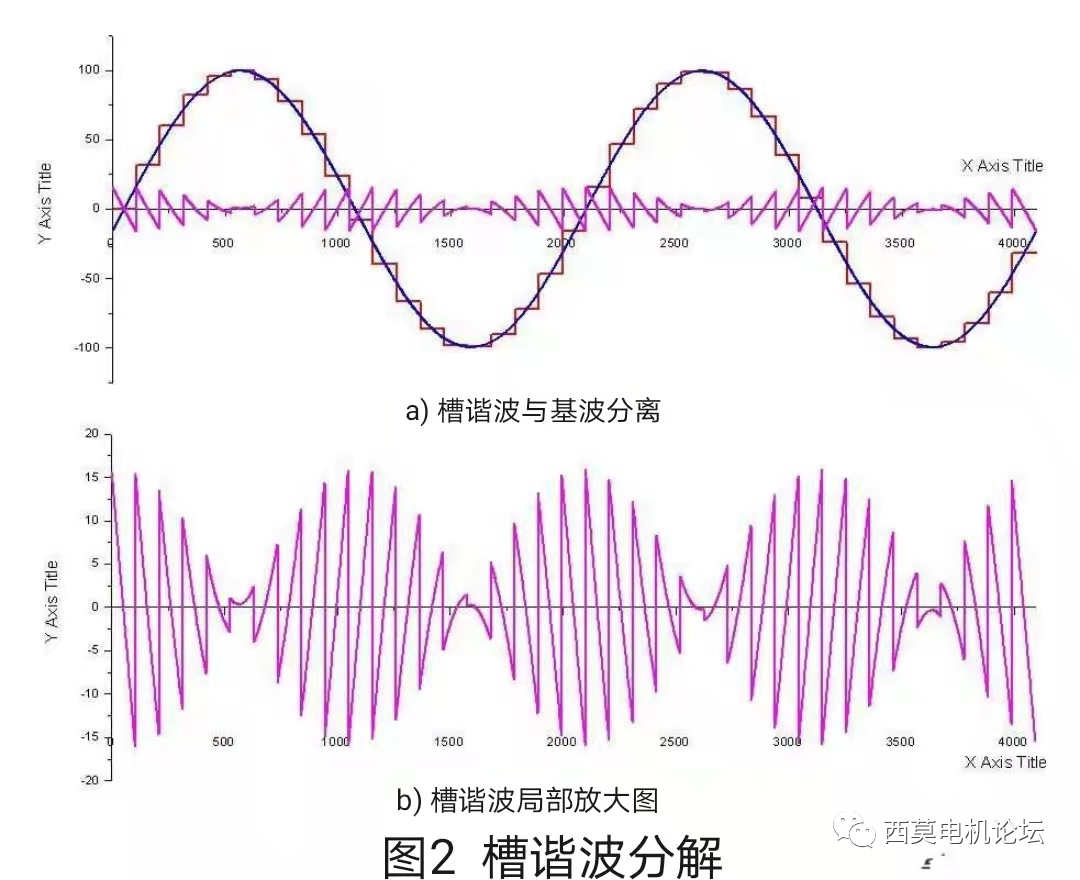
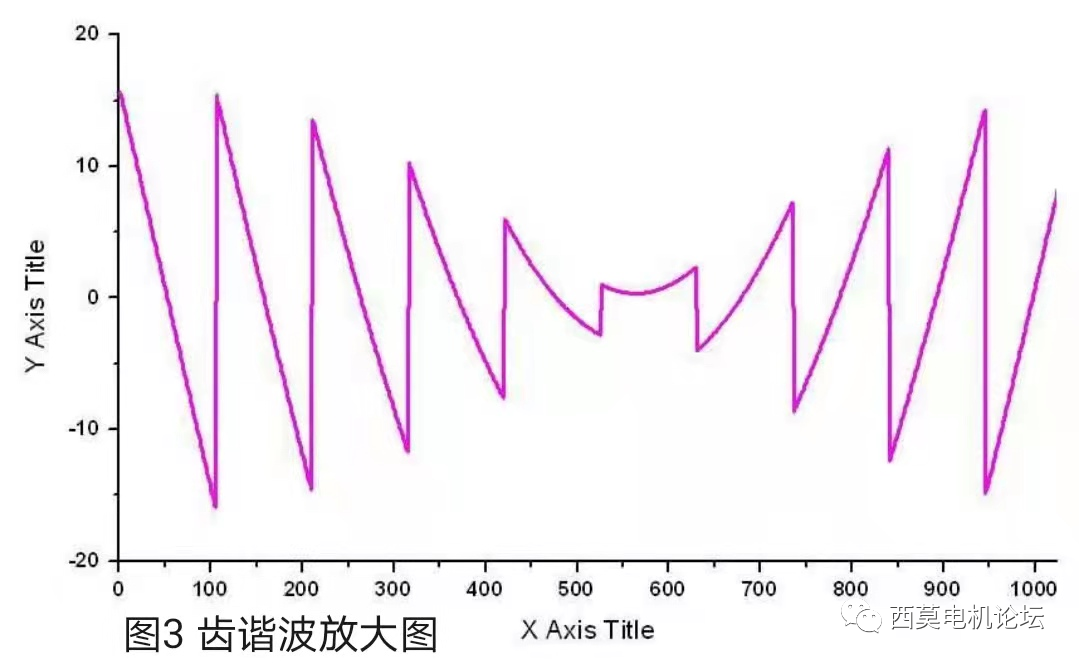
進一步分析槽諧波的波形,其斜線部分并非直線,其實仔細想一想就會明白,槽諧波是實際的臺階磁勢曲線與理想正弦波曲線的差值,因此斜線其實應該是正弦曲線形狀,這點在靠近主波的波峰時表現得尤為明顯!
以上分析了槽諧波的產生機理和槽諧波的波形,顯然要想減小槽諧波,就必須增加槽數使臺階數量增加,而且使每個臺階的躍升高度更加逼近基波正弦曲線,直至槽數增加到無窮大,這樣就完全沒有了槽諧波。但在實際電機中,槽數無窮大是不可能的,通常電機中槽數是有限的,因此槽諧波也是永遠會存在的。
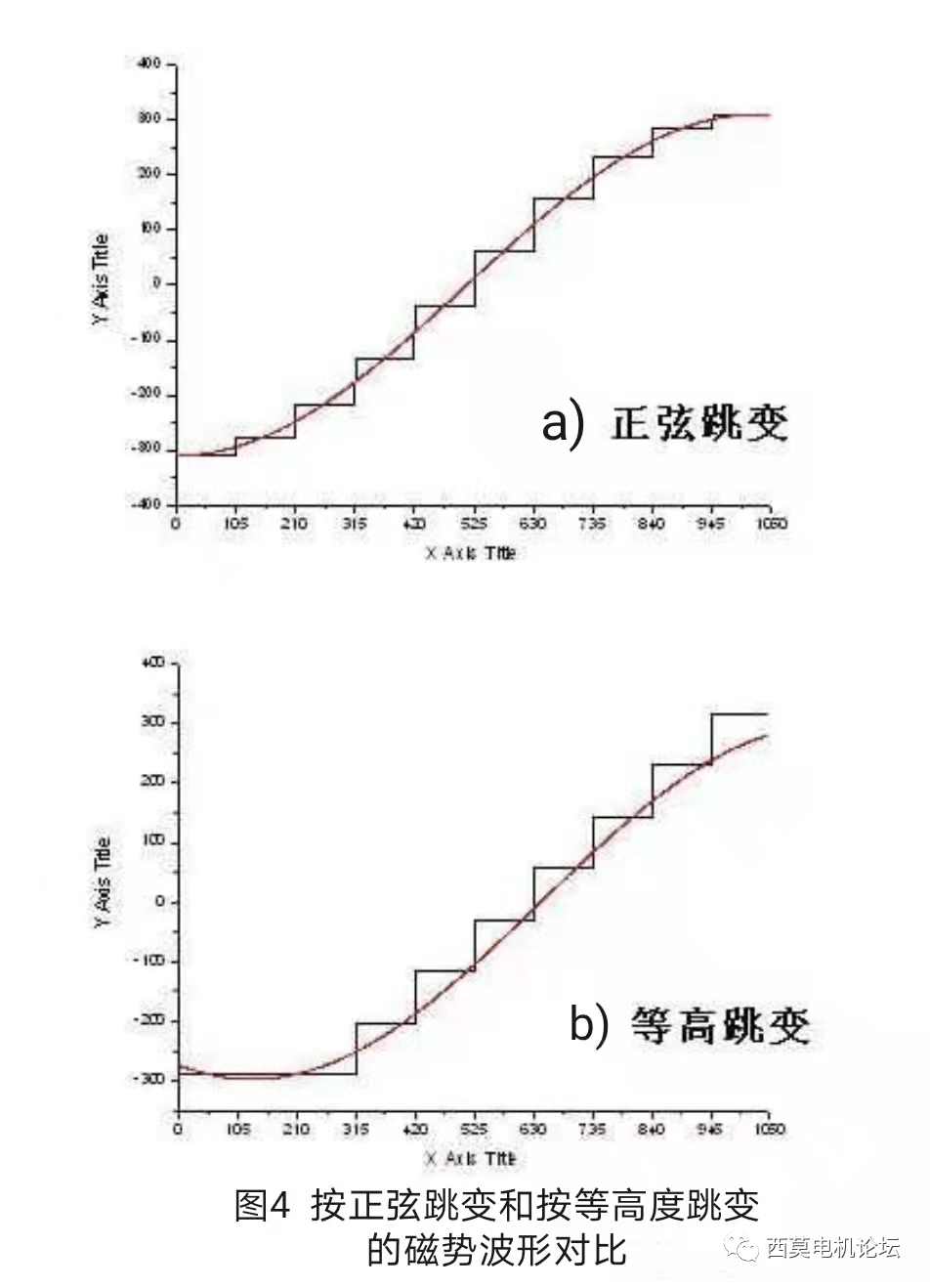
另外除了電機的槽數不可能很多,電機的相數更不可能很多。以上討論了每個槽內的電流相位都不相同,即槽數和相數相等,每個槽都是獨立一相的情況,在這種情況下沒有相帶諧波,只有槽諧波。實際電機中不可能有很多相,否則電源系統會非常復雜,也就是說相數總是小于槽數的。這就意味著有相鄰的幾個槽內電流相位相同,任意時刻這幾個槽內的電流大小相等,這就需要引入“相帶”的概念。通俗地講,對幾個槽通入相同相位的電流,也就是把幾個槽設計成同一個數學相,這樣同屬一個數學相的槽就組成了一個相帶,同一個相帶中各槽內的電流相等,因此同一個相帶內各槽磁勢的跳變臺階高度就相同。本來每個槽中的電流應該具有不同的相位,現在由于物理實現上面的局限而強行變成了相同的電流相位,磁勢波形變成了等高度跳變,這就是相帶諧波產生的根源!如圖4所示,圖4a)為上例中在一個極距范圍內各槽不同相位時,磁勢按正弦規律跳變的情況;圖4b)為在一個極距范圍內各槽都屬于同一相,磁勢按等高度跳變的情況。兩種情況下的磁勢波形對比,顯然圖4a)按正弦規律跳變的磁勢波形更加逼近正弦基波,而圖4b)按等高度跳變的階梯波形偏離基波正弦曲線更大,由此說明圖4a)里僅包含了槽諧波,無相帶諧波;而圖4b)里不僅包含了槽諧波還包括了相帶諧波。
 如果槽數無窮多,相帶數也是無窮多,那么磁勢波形就不會有槽諧波,也不會有相帶諧波,這是電機中最為理想的電流分布狀態!遺憾的是,實際的電機,往往都是槽數有限,而且相帶數比槽數更少,因此磁勢中就既含有槽諧波又含有相帶諧波!
如果槽數無窮多,相帶數也是無窮多,那么磁勢波形就不會有槽諧波,也不會有相帶諧波,這是電機中最為理想的電流分布狀態!遺憾的是,實際的電機,往往都是槽數有限,而且相帶數比槽數更少,因此磁勢中就既含有槽諧波又含有相帶諧波!
綜上所述可以得到以下結論:
①相帶諧波就是電流相位不均布于整個圓周導致的,更準確的說法是,只要相數少于槽數,就必然有相帶諧波。
②槽數無限、相數無限時無諧波。
③槽數無限、相數有限時只有相帶諧波而無槽諧波。
④槽數有限、相數等于槽數時只有槽諧波而無相帶諧波。
⑤槽數有限、相數小于槽數時即有槽諧波也有相帶諧波,這是通常電機最常見的情況。
應該指出的一點是,無論是槽諧波還是相帶諧波,其波形都是隨時變化的,這點可以這樣來理解:因為一個相帶占用的空間角度很大從而是突變的,而電流相位卻是無限連續的,也就是兩者之間無法做到總是相匹配。以上圖1~4,是某相電流達到最大值時刻的狀態,在其他時刻,磁勢波形會有一些變化,從而導致齒諧波和相帶諧波也會有稍許的不同。
4 磁勢諧波的削弱方法及內在機理
通過以上兩篇文章的分析,我們知道了磁勢諧波包括相帶諧波和槽諧波兩種,而且也了解了產生相帶諧波和槽諧波的機理。要想削弱磁勢諧波,就要從產生這兩種諧波的成因入手。
4.1 槽諧波的削弱
如上所述,要想削弱槽諧波就必須增加槽數。其實這就是通過加大繞組的分布來削弱槽諧波的內在本質。當然,增加槽數會帶來槽利用率的降低和槽絕緣材料的增加,況且電機的槽數受多種因素制約,不可能無限制地增加;另外增加槽數加大繞組的分布,會在削弱槽諧波的同時也削弱了基波磁勢的幅值,因為繞組的槽諧波分布系數與基波分布系數相等。因此槽諧波的削弱是比較困難的,效果也是有限的,而且還會付出一定的代價,我們只能在權衡各方面利弊的情況下,盡量增加槽數,減小槽諧波。
另外我們經常說通過斜槽可以削弱齒諧波,其實通過前面的論述可知,對于某一特定的軸向截面而言,斜槽并不能削弱該位置的槽諧波,只不過是通過使槽諧波的空間相位沿軸向產生一定程度的相位移,這對繞組感應電勢中的齒諧波的確會產生非常大的削弱作用。對磁勢的槽諧波并無明顯的削弱效果。
通常人們津津樂道削弱齒諧波的方法還有采用分數槽,但分數槽對削弱某些次數的齒諧波,也就是電勢中的齒諧波的確有著明顯效果,關于這一點已在前面電勢諧波的相關文章中進行過詳述,在此不再贅述。而對于槽諧波,也就是磁勢中的諧波就一言難盡了,有關分數槽繞組的磁勢諧波問題,將在下一期中詳細論述。
4.2 相帶諧波的削弱
如前所述,相帶諧波是由于相帶劃分而產生的諧波。要想削弱相帶諧波,就必須增加繞組的數學相數,特別是每對極下的數學相數。當然物理相數的增加總是對增加數學相數有利的,但物理相數的增加必然帶來電源系統的復雜性,需要付出一定的代價。我們需要重點考慮的是,如何在物理相數一定的情況下盡量增加數學相數,這樣代價會小很多。例如如何在最常見的三相繞組基礎上增加數學相數。雙層短距繞組就是一種最好的措施,沒有之一!
前面我們重點對單層繞組的相帶諧波進行了分析。對于雙層繞組,可以把上下兩層導體分別看做兩個獨立的單層繞組。如果是雙層整距繞組,則同一槽中的上下層導體均屬同一相,這種情況的相帶和數學相數與單層繞組的情況相同,如圖5所示。可見三相60o相帶繞組每對極共有六個相帶,即數學相數為6。
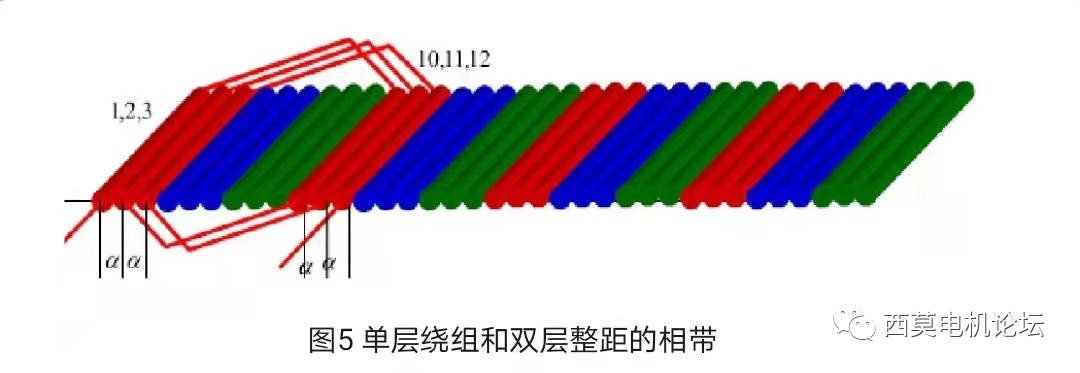 若繞組為雙層短距繞組,則意味著上下層所分別表示的兩個單層繞組錯開了一定的短距角,短距不同錯開的角度就不同,如圖6所示。
若繞組為雙層短距繞組,則意味著上下層所分別表示的兩個單層繞組錯開了一定的短距角,短距不同錯開的角度就不同,如圖6所示。
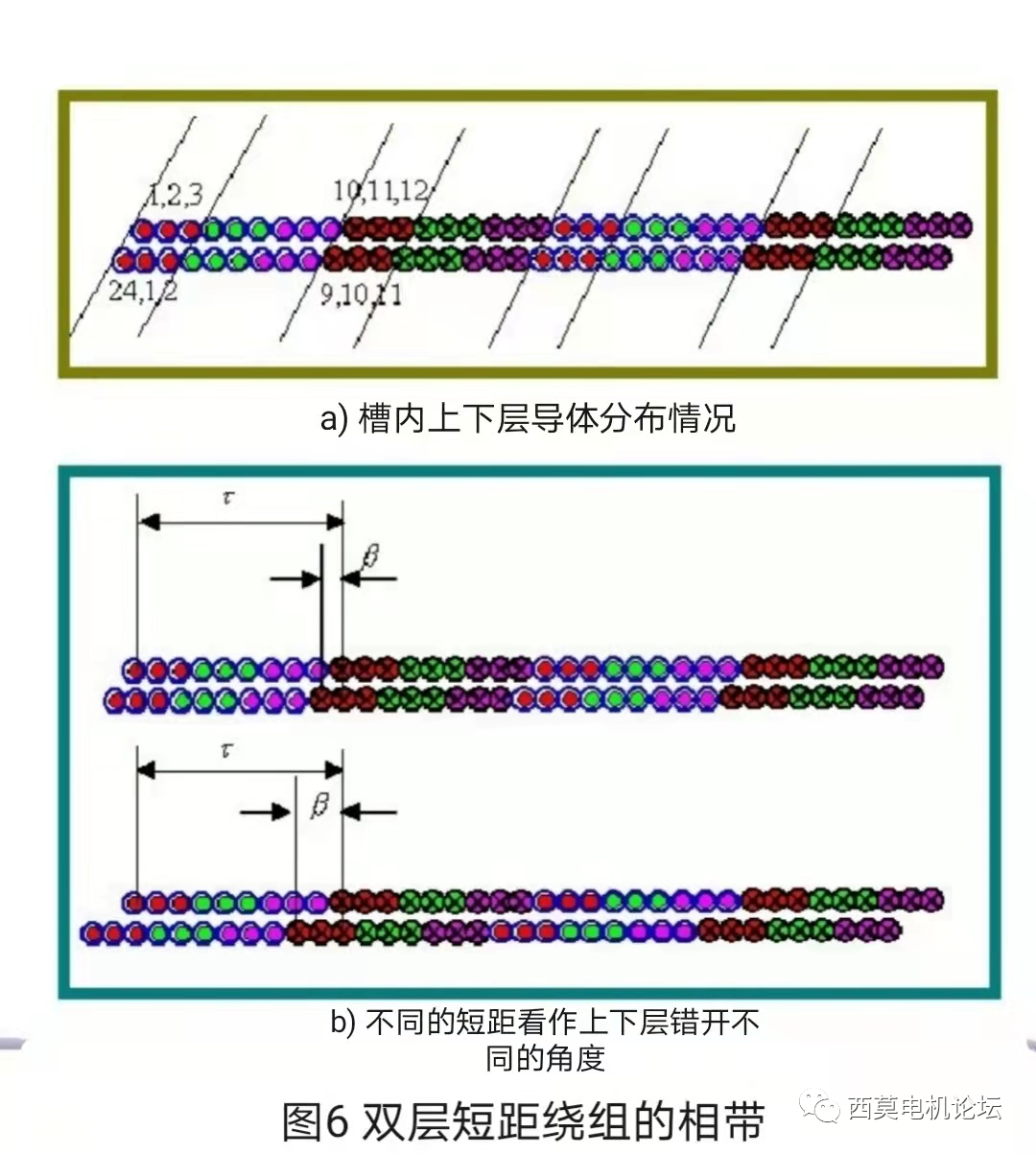
圖6a)表示短一個槽時槽內導體的分布情況,此時有些槽內上下層導體屬于同一相,而有些槽內上下層導體屬于不同的相,上下層導體屬于同一相的槽安導數為兩個導體安導之和,即為一層導體安導數的2倍,而上下層導體屬于不同相的槽內安導數為兩相導體安導之代數和。這樣就使得磁勢在經過不同槽時跳變的高度不同,相當于數學相數或相帶數就比單層繞組或雙層整距繞組變多了,從而實現了同樣的物理相數卻增多了數學相數或相帶數的目的。由圖6不難看出,雙層短距后每對極的數學相數較單層繞組增加了一倍。圖6b)示出了不同短距時上下層導體錯開的角度,通過不同的短距,可以實現不同數學相的相帶寬度,從而實現削弱不同次數的相帶諧波。如果所短的距離正好是某次相帶諧波的半個波長,則可以完全消除該次諧波。這就是短距繞組削弱相帶諧波的內在機理。通常三相繞組設計時為了同時削弱5次和7次相帶諧波,常采用5/6短距設計。
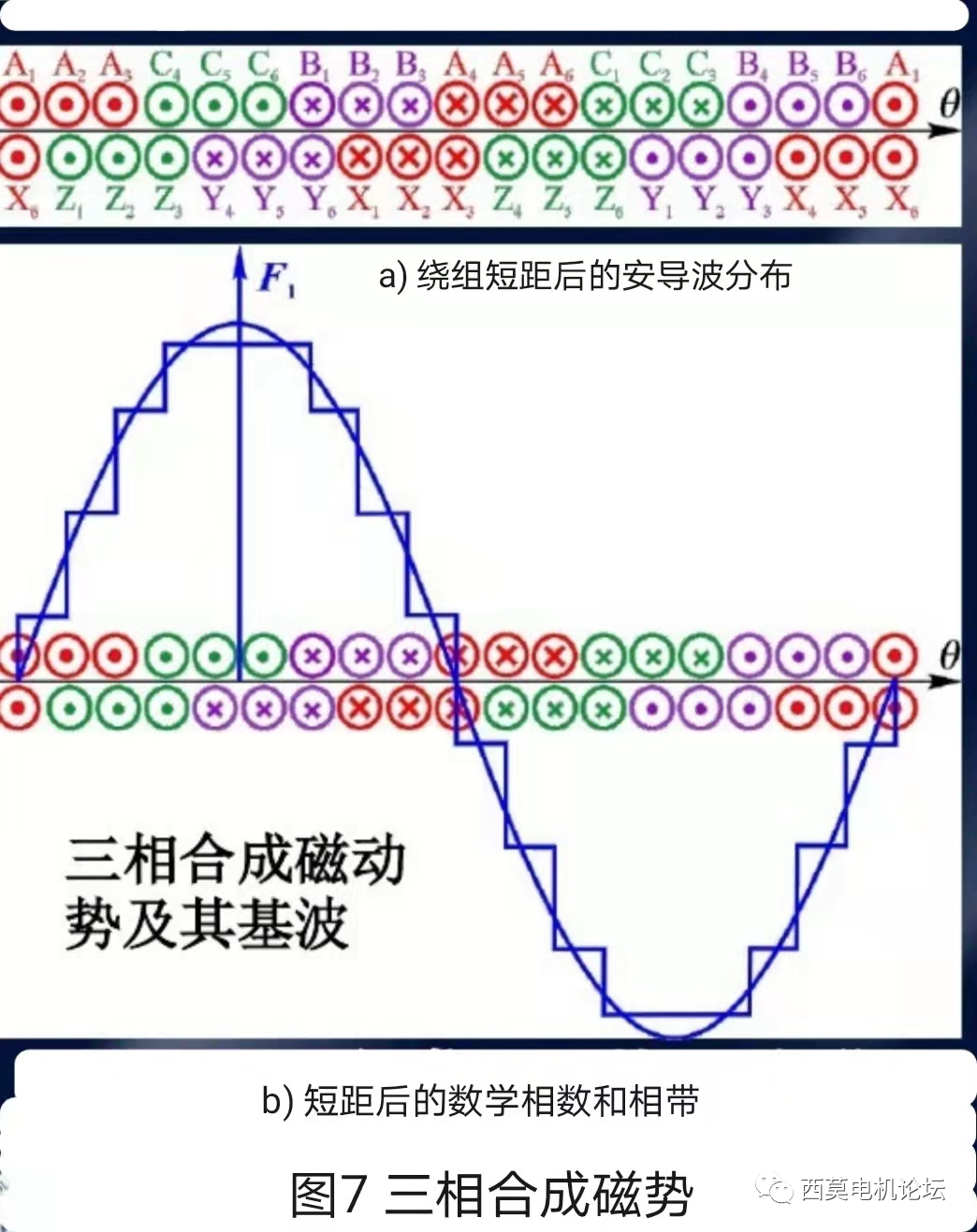
如圖7所示為三相雙層短距繞組的合成磁勢,顯然合成磁勢臺階跳變高度的數目比單層繞組多出了一倍,說明短距增多了數學相數。
以上通過兩篇文章,我們詳細論述了繞組磁勢的相帶諧波和槽諧波。在本文的寫作過程中,參考了西莫電機論壇里第二期研討會——氣隙磁場專題的有關帖子,采納了其中一些網友的觀點,特別是曾曉東老師的許多觀點和論述,對本文貢獻很大,而且文中部分圖片也截自他所貼出的圖片,在此對這些文獻的原作者表示衷心感謝!本期內容就到這里,下期講分數槽繞組的磁勢,敬請期待!
審核編輯:湯梓紅
-
電機
+關注
關注
143文章
9248瀏覽量
148327 -
諧波
+關注
關注
7文章
865瀏覽量
42443 -
繞組
+關注
關注
2文章
531瀏覽量
20154
原文標題:電機繞組(十六)
文章出處:【微信號:西莫電機論壇,微信公眾號:西莫電機論壇】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
【EMC家園】諧波抑制與利用!
淺談三相繞組磁勢及其合成磁勢基波
變頻電源應該如何抑制諧波
電視的諧波電流和抑制技術分析
逆變電源中的諧波抑制
諧波的抑制與利用
微電網諧波傳播抑制
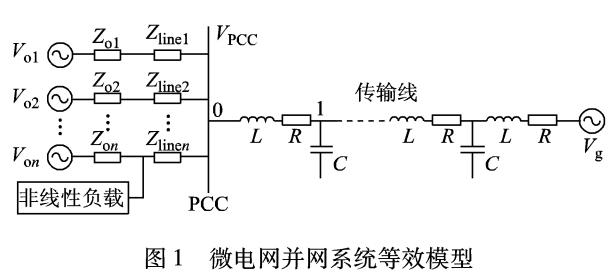





 繞組磁勢諧波的影響因素與諧波抑制
繞組磁勢諧波的影響因素與諧波抑制











評論