均方根值（RMS）和平方和的根值（RSS）是兩個(gè)相關(guān)的概念，它們?cè)跀?shù)學(xué)上有相似之處，也有各自的適用范圍，但絕不能混為一談。

想象一個(gè)場景，我們?cè)跁r(shí)間T1時(shí)刻對(duì)某個(gè)負(fù)載電阻施加電壓E1。在此過程中會(huì)有一些功率耗散。該功率為P=E12/R。然后，在T2時(shí)刻，我們施加E2，得到E22/R，然后在時(shí)間T3時(shí)刻，我們施加E3，得到E32/R，以此類推。

如果我們將時(shí)間標(biāo)記保持緊密間隔，并且對(duì)從T1到Tn的時(shí)間執(zhí)行同樣的操作，我們將獲得E1到En的平方和，即E12+E22+E32+…+En2，這是傳遞到該電阻R的功率之和。獲得該總和后，我們將該總和除以n以獲得平均值，我們可以將其稱為“平方和”的平均值。接下來，我們?nèi)　捌椒胶汀逼骄档钠椒礁@樣我們就找到了施加在R上的電壓的RMS。

如果我們一直重復(fù)、重復(fù)、再重復(fù)施加電壓的序列，那么RMS值就是穩(wěn)定地施加到R上的電壓，其功率輸出和熱效應(yīng)與我們一直在討論的電壓施加序列相同。適用的計(jì)算公式也是我們非常熟悉的：

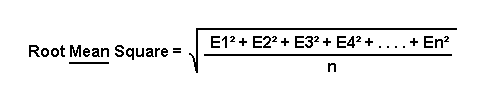
“平方和的根”也就是RSS，與RMS看起來很相似，但概念截然不同。RSS的計(jì)算公式如下：

這兩個(gè)概念之間的區(qū)別在于我們是否將總和或平方和除以“n”。 RSS與功率水平無關(guān)，但在微波系統(tǒng)分析中確實(shí)有應(yīng)用。

所有微波系統(tǒng)都是由一些級(jí)聯(lián)設(shè)備組成的，在每個(gè)設(shè)備間的接口處，都會(huì)存在一定駐波比（SWR）。如果每個(gè)設(shè)備的功率都是無損的，那么級(jí)聯(lián)中的SWR就會(huì)產(chǎn)生一個(gè)復(fù)合系統(tǒng)的總駐波比，這個(gè)駐波比名義上是這些單個(gè)SWR的乘積。

很不幸的是，當(dāng)我們?cè)噲D估算出最壞情況下總駐波比的計(jì)算結(jié)果時(shí)，如果將其作為單個(gè)SWR的乘積，所得出的數(shù)字可能會(huì)高得離譜。在這種情況下，有時(shí)會(huì)決定將總駐波比的最壞情況估計(jì)為各個(gè)SWR的RSS。

請(qǐng)看圖1中的圖示：

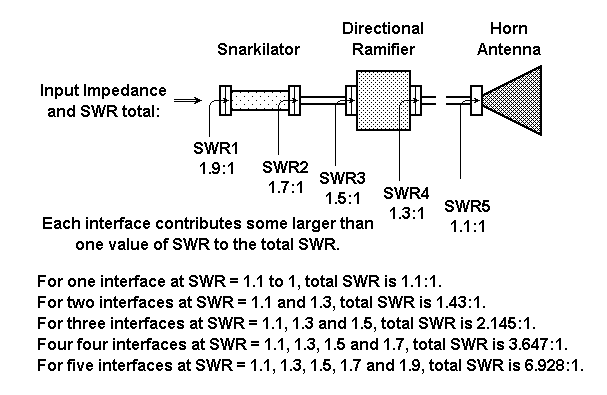
圖1 設(shè)置總駐波比是設(shè)備間SWR的乘積。資料來源：John Dunn

只是編造一些可笑的設(shè)備名稱，顯示了1到5個(gè)設(shè)備間接口的計(jì)算，然后將這些值與圖2中的RSS進(jìn)行比較。

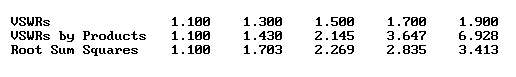
圖2 1到5個(gè)設(shè)備間接口的乘積與RSS的比較。資料來源：John Dunn

總駐波比的RSS并不總是小于SWR乘積的計(jì)算結(jié)果，但有時(shí)會(huì)小于。對(duì)于圖示的設(shè)備間SWR，RSS結(jié)果對(duì)于具有四個(gè)和五個(gè)接口的情況較小。

SWR為6.928:1的可能性非常小，因此在現(xiàn)實(shí)世界中，這樣的結(jié)果可能會(huì)被視為不切實(shí)際。相比之下，3.413:1的SWR很可能是現(xiàn)實(shí)世界中最壞情況下SWR值的真實(shí)測量值。

我的客戶不僅接受了這種解釋，而且實(shí)際上也一直堅(jiān)持這樣計(jì)算。