的基礎知識,講述了確定性數字信號處理的知識,包括離散時間信號及系統的介紹、z變換、傅里葉變換、頻率分析以及濾波器設計等。介紹了隨機數字信號處理的知識,主要學習多速率數字信號處理、線性預
發表于 04-07 16:41
頻域示波器,其主要技術原理基于信號的傅里葉變換理論,通過快速傅里葉變換(FFT)算法將時域信號轉換為頻域信號,從而進行頻譜分析。以下是對
發表于 03-11 14:37
DFT與離散時間傅里葉變換(DTFT)的關系 DFT(離散傅里葉變換)與DTFT(離散時間傅里葉變換)都是信號處理中的重要工具,用于將信號從時域轉換到頻域。它們之間存在一定的聯系和區別
![的頭像]() 發表于
發表于 12-20 09:21
?1401次閱讀
使用離散傅里葉變換(DFT)進行頻譜分析是一個將信號從時域轉換到頻域,并分析信號在頻域上的特性的過程。以下是使用DFT進行頻譜
![的頭像]() 發表于
發表于 12-20 09:16
?1648次閱讀
解和分析信號的特性。 具體來說,時域信號是描述信號隨時間變化的函數,而頻域信號則是描述信號隨頻率變化的函數。傅里葉變換建立了時域信號和頻域信號之間的橋梁,使得我們可以從頻率的角度去
![的頭像]() 發表于
發表于 12-06 17:02
?1105次閱讀
和離散傅里葉變換。 傅里葉變換的核心思想是將一個復雜的信號或函數表示為多個不同頻率的正弦波和余弦波的疊加。這樣,原本在時域或空間域中難以分析的復雜信號,就可以在頻域中清晰地看到其組成的
![的頭像]() 發表于
發表于 12-06 16:48
?1282次閱讀
傅里葉變換是一種數學工具,用于將信號從時域轉換到頻域,以便分析其頻率成分。在使用傅里葉變換時,可能會遇到一些常見的錯誤。 1. 采樣定理錯誤
![的頭像]() 發表于
發表于 11-14 09:42
?1993次閱讀
傅里葉變換是信號處理和分析中的一項基本工具,它能夠將一個信號從時間域(或空間域)轉換到頻率域。以下是傅里葉變換的基本性質和定理: 一、基本性質 線性性質 : 傅里葉變換是線性的,即對于
![的頭像]() 發表于
發表于 11-14 09:39
?2723次閱讀
經典傅里葉變換與快速傅里葉變換(FFT)在多個方面存在顯著的區別,以下是對這兩者的比較: 一、定義與基本原理 經典傅里葉變換 : 是一種將滿足一定條件的某個函數表示成三角函數(正弦和/或余弦函數
![的頭像]() 發表于
發表于 11-14 09:37
?1110次閱讀
復雜度較高,為O(n^2)。具體步驟如下: 對于長度為N的離散信號x(n),其離散傅里葉變換X(k)定義為: X(k)=∑[n=0 to N-1] x(n)W_N^(kn),其中W_N=exp(-j2
![的頭像]() 發表于
發表于 11-14 09:35
?1154次閱讀
傅里葉變換與卷積定理之間存在著密切的關系,這種關系在信號處理、圖像處理等領域中具有重要的應用價值。 一、傅里葉變換與卷積的基本概念 傅里葉變換 : 是一種將時間域(或空間域)信號轉換為頻率域信號
![的頭像]() 發表于
發表于 11-14 09:33
?1714次閱讀
在數字信號處理和圖像分析領域,傅里葉變換和圖像處理技術是兩個核心概念。盡管它們在實際應用中常常交織在一起,但它們在本質上有著明顯的區別。 傅里葉變換的基本原理 傅里葉變換是一種將信號從
![的頭像]() 發表于
發表于 11-14 09:30
?756次閱讀
在現代通信和信號處理領域,傅里葉變換(FT)扮演著核心角色。它不僅幫助我們分析信號的頻率成分,還能用于濾波、壓縮和信號恢復等多種任務。 傅里葉變換的基本原理 傅里葉變換是一種將信號從時
![的頭像]() 發表于
發表于 11-14 09:29
?4372次閱讀
傅里葉變換的數學原理主要基于一種將函數分解為正弦和余弦函數(或復指數函數)的線性組合的思想。以下是對傅里葉變換數學原理的介紹: 一、基本原理 傅里葉級數 :對于周期性連續信號,可以將其表示為傅里葉
![的頭像]() 發表于
發表于 11-14 09:27
?1535次閱讀
數字信號處理是電子工程和信息科學領域的一個重要分支,它涉及到對信號進行分析、處理和轉換的方法。數字信號處理的三大變換關系是傅里葉變換、拉普拉斯變換和Z
![的頭像]() 發表于
發表于 08-09 09:33
?2285次閱讀
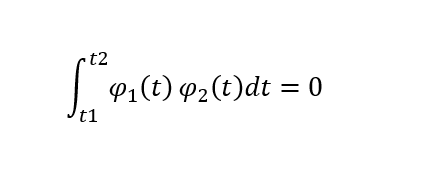
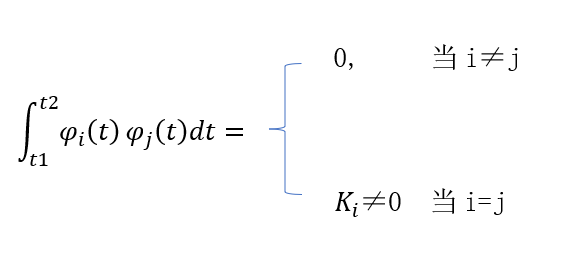

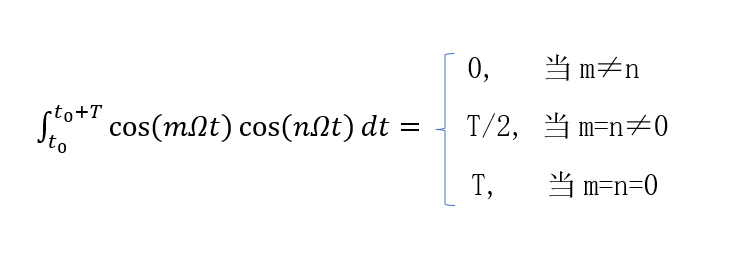
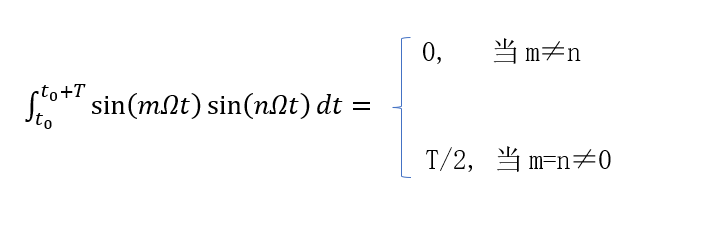
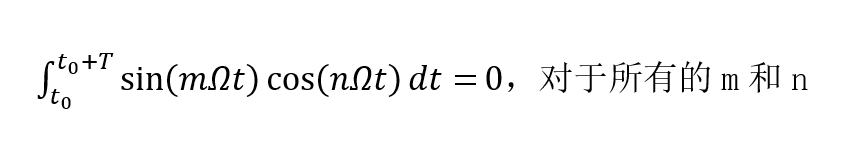
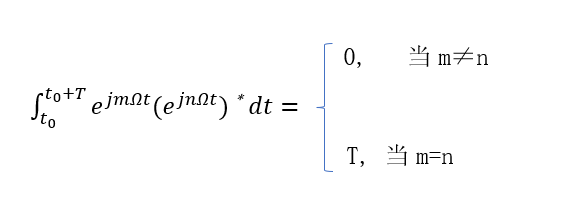








 傅里葉變換和系統的頻域分析(1)
傅里葉變換和系統的頻域分析(1)










評論