傅里葉變換與時(shí)域信號(hào)的關(guān)系
傅里葉變換是一種數(shù)學(xué)工具,它能夠?qū)r(shí)域信號(hào)(即隨時(shí)間變化的信號(hào))轉(zhuǎn)換為頻域信號(hào)(即隨頻率變化的信號(hào)),或者將頻域信號(hào)轉(zhuǎn)換回時(shí)域信號(hào)。這種轉(zhuǎn)換關(guān)系使得我們能夠更加深入地理解和分析信號(hào)的特性。
具體來說,時(shí)域信號(hào)是描述信號(hào)隨時(shí)間變化的函數(shù),而頻域信號(hào)則是描述信號(hào)隨頻率變化的函數(shù)。傅里葉變換建立了時(shí)域信號(hào)和頻域信號(hào)之間的橋梁,使得我們可以從頻率的角度去分析時(shí)域信號(hào)。通過傅里葉變換,我們可以得到信號(hào)的頻譜,即信號(hào)在不同頻率下的分量及其幅值和相位信息。
傅里葉變換在音頻信號(hào)處理中的應(yīng)用
傅里葉變換在音頻信號(hào)處理中發(fā)揮著至關(guān)重要的作用。以下是傅里葉變換在音頻信號(hào)處理中的一些主要應(yīng)用:
- 頻譜分析 :
- 通過傅里葉變換,我們可以將音頻信號(hào)從時(shí)域轉(zhuǎn)換到頻域,從而分析信號(hào)中不同頻率成分的強(qiáng)度和分布。
- 這在語(yǔ)音識(shí)別、樂器聲音分析、環(huán)境噪聲監(jiān)測(cè)等領(lǐng)域是一項(xiàng)基本的工具。例如,在音樂信號(hào)處理中,通過傅里葉變換我們可以分析出音樂信號(hào)的基頻、諧波結(jié)構(gòu)以及不同音符對(duì)應(yīng)的頻率分量。
- 濾波器設(shè)計(jì) :
- 回聲與混響消除 :
- 在語(yǔ)音通信系統(tǒng)中,回聲和混響是常見的干擾因素,影響通話質(zhì)量。
- 傅里葉變換在回聲與混響消除算法中發(fā)揮了關(guān)鍵作用。通過分析回聲的頻譜特性,設(shè)計(jì)頻域?yàn)V波器或自適應(yīng)濾波器,可以有效減少或消除回聲和混響。
- 音頻壓縮 :
- 音頻壓縮技術(shù)如MP3、AAC等利用了人耳對(duì)不同頻率的敏感度差異,通過傅里葉變換分析音頻信號(hào)的頻譜,將不重要的頻率分量丟棄或壓縮,從而大幅降低音頻文件的大小。
- 在這些壓縮算法中,傅里葉變換用于識(shí)別并量化音頻信號(hào)的頻譜成分,使得壓縮后的音頻在保持音質(zhì)的同時(shí)極大地減少了數(shù)據(jù)量。
- 短時(shí)傅里葉變換(STFT) :
- STFT是傅里葉變換的擴(kuò)展,適用于處理非平穩(wěn)信號(hào)。它將信號(hào)分成多個(gè)短時(shí)段,并對(duì)每個(gè)時(shí)段進(jìn)行傅里葉變換,從而得到信號(hào)隨時(shí)間變化的頻率成分。
- STFT的結(jié)果通常以語(yǔ)譜圖的形式展示,即頻率隨時(shí)間的變化圖。語(yǔ)譜圖廣泛應(yīng)用于語(yǔ)音識(shí)別、音頻效果分析、聲源定位等領(lǐng)域。
綜上所述,傅里葉變換在音頻信號(hào)處理中具有廣泛的應(yīng)用和重要的作用。它為我們提供了一種從時(shí)間域到頻率域的視角,使得我們能夠更加全面地理解和處理音頻信號(hào)。
-
函數(shù)
+關(guān)注
關(guān)注
3文章
4371瀏覽量
64228 -
傅立葉變換
+關(guān)注
關(guān)注
3文章
105瀏覽量
32793 -
音頻信號(hào)處理
+關(guān)注
關(guān)注
0文章
9瀏覽量
1737
發(fā)布評(píng)論請(qǐng)先 登錄
連續(xù)時(shí)間信號(hào)與系統(tǒng)的傅立葉分析
傅立葉變換的性質(zhì) (ppt教案)
進(jìn)行傅立葉變換的原因、定義、物理意義簡(jiǎn)述
信號(hào)時(shí)域和頻域及快速傅立葉變換與加窗信號(hào)的詳細(xì)講解

簡(jiǎn)述FPGA的快速傅立葉變換
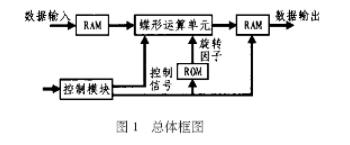





 傅立葉變換與時(shí)域信號(hào)的關(guān)系 傅立葉變換在音頻信號(hào)處理中的應(yīng)用
傅立葉變換與時(shí)域信號(hào)的關(guān)系 傅立葉變換在音頻信號(hào)處理中的應(yīng)用










評(píng)論