到目前為止,我們實現的每個模型都需要我們根據一些預先指定的分布來初始化它的參數。直到現在,我們都認為初始化方案是理所當然的,掩蓋了如何做出這些選擇的細節。您甚至可能覺得這些選擇并不是特別重要。相反,初始化方案的選擇在神經網絡學習中起著重要作用,對于保持數值穩定性至關重要。此外,這些選擇可以以有趣的方式與非線性激活函數的選擇聯系起來。我們選擇哪個函數以及我們如何初始化參數可以決定我們的優化算法收斂的速度。這里的錯誤選擇可能會導致我們在訓練時遇到梯度爆炸或消失的情況。在這個部分,
%matplotlib inline import torch from d2l import torch as d2l
%matplotlib inline from mxnet import autograd, np, npx from d2l import mxnet as d2l npx.set_np()
%matplotlib inline import jax from jax import grad from jax import numpy as jnp from jax import vmap from d2l import jax as d2l
No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)
%matplotlib inline import tensorflow as tf from d2l import tensorflow as d2l
5.4.1. 消失和爆炸梯度
考慮一個深度網絡L圖層,輸入x 和輸出o. 每層l由轉換定義fl權重參數化 W(l), 隱藏層輸出為 h(l)(讓h(0)=x),我們的網絡可以表示為:
(5.4.1)h(l)=fl(h(l?1))and thuso=fL°…°f1(x).
如果所有隱藏層的輸出和輸入都是向量,我們可以寫出梯度為o關于任何一組參數 W(l)如下:
(5.4.2)?W(l)o=?h(L?1)h(L)?M(L)=def?…??h(l)h(l+1)?M(l+1)=def?W(l)h(l)?v(l)=def.
換句話說,這個梯度是L?l矩陣 M(L)?…?M(l+1)和梯度向量v(l). 因此,當將太多概率相乘時,我們很容易遇到同樣的數值下溢問題。在處理概率時,一個常見的技巧是切換到對數空間,即將壓力從尾數轉移到數值表示的指數。不幸的是,我們上面的問題更嚴重:最初矩陣 M(l)可能有各種各樣的特征值。它們可能很小或很大,它們的產品可能很大或 很小。
不穩定梯度帶來的風險超出了數值表示。不可預測的梯度也會威脅到我們優化算法的穩定性。我們可能面臨以下參數更新:(i) 過大,破壞了我們的模型( 梯度爆炸問題);或 (ii) 過小(梯度消失問題),由于參數幾乎不會在每次更新時移動,因此無法進行學習。
5.4.1.1。消失的漸變
導致梯度消失問題的一個常見罪魁禍首是激活函數的選擇σ在每一層的線性操作之后附加。從歷史上看,sigmoid 函數1/(1+exp?(?x))(在第 5.1 節中介紹)很受歡迎,因為它類似于閾值函數。由于早期的人工神經網絡受到生物神經網絡的啟發,神經元要么完全放電要么根本不放電(就像生物神經元一樣)的想法似乎很有吸引力。讓我們仔細看看 sigmoid,看看它為什么會導致梯度消失。
x = torch.arange(-8.0, 8.0, 0.1, requires_grad=True)
y = torch.sigmoid(x)
y.backward(torch.ones_like(x))
d2l.plot(x.detach().numpy(), [y.detach().numpy(), x.grad.numpy()],
legend=['sigmoid', 'gradient'], figsize=(4.5, 2.5))
x = np.arange(-8.0, 8.0, 0.1) x.attach_grad() with autograd.record(): y = npx.sigmoid(x) y.backward() d2l.plot(x, [y, x.grad], legend=['sigmoid', 'gradient'], figsize=(4.5, 2.5))
[07:15:48] src/base.cc:49: GPU context requested, but no GPUs found.
x = jnp.arange(-8.0, 8.0, 0.1)
y = jax.nn.sigmoid(x)
grad_sigmoid = vmap(grad(jax.nn.sigmoid))
d2l.plot(x, [y, grad_sigmoid(x)],
legend=['sigmoid', 'gradient'], figsize=(4.5, 2.5))
x = tf.Variable(tf.range(-8.0, 8.0, 0.1))
with tf.GradientTape() as t:
y = tf.nn.sigmoid(x)
d2l.plot(x.numpy(), [y.numpy(), t.gradient(y, x).numpy()],
legend=['sigmoid', 'gradient'], figsize=(4.5, 2.5))
如您所見,S 形函數的梯度在其輸入較大和較小時都消失了。此外,當通過多層反向傳播時,除非我們處于 Goldilocks 區,其中許多 sigmoid 的輸入接近于零,否則整個產品的梯度可能會消失。當我們的網絡擁有很多層時,除非我們小心,否則梯度可能會在某一層被切斷。事實上,這個問題曾經困擾著深度網絡訓練。因此,更穩定(但在神經上不太可信)的 ReLU 已成為從業者的默認選擇。
5.4.1.2. 爆炸梯度
相反的問題,當梯度爆炸時,可能同樣令人煩惱。為了更好地說明這一點,我們繪制了 100 個高斯隨機矩陣并將它們與某個初始矩陣相乘。對于我們選擇的尺度(方差的選擇σ2=1), 矩陣乘積爆炸。當由于深度網絡的初始化而發生這種情況時,我們沒有機會讓梯度下降優化器收斂。
M = torch.normal(0, 1, size=(4, 4))
print('a single matrix n',M)
for i in range(100):
M = M @ torch.normal(0, 1, size=(4, 4))
print('after multiplying 100 matricesn', M)
a single matrix
tensor([[ 0.0837, -0.9784, -0.5752, -0.0418],
[ 2.0032, 2.0948, -1.4284, -1.5950],
[-0.9720, -2.1672, -0.2809, 0.2282],
[-0.7581, 0.0328, -0.2364, -0.5804]])
after multiplying 100 matrices
tensor([[ 7.5119e+24, -9.2313e+24, -2.1761e+24, 7.0456e+23],
[-1.3462e+24, 1.6544e+24, 3.8999e+23, -1.2627e+23],
[ 1.4648e+25, -1.8001e+25, -4.2433e+24, 1.3739e+24],
[ 8.9242e+24, -1.0967e+25, -2.5852e+24, 8.3702e+23]])
M = np.random.normal(size=(4, 4))
print('a single matrix', M)
for i in range(100):
M = np.dot(M, np.random.normal(size=(4, 4)))
print('after multiplying 100 matrices', M)
a single matrix [[ 2.2122064 1.1630787 0.7740038 0.4838046 ] [ 1.0434403 0.29956347 1.1839255 0.15302546] [ 1.8917114 -1.1688148 -1.2347414 1.5580711 ] [-1.771029 -0.5459446 -0.45138445 -2.3556297 ]] after multiplying 100 matrices [[ 3.4459747e+23 -7.8040759e+23 5.9973355e+23 4.5230040e+23] [ 2.5275059e+23 -5.7240258e+23 4.3988419e+23 3.3174704e+23] [ 1.3731275e+24 -3.1097129e+24 2.3897754e+24 1.8022945e+24] [-4.4951091e+23 1.0180045e+24 -7.8232368e+23 -5.9000419e+23]]
get_key = lambda: jax.random.PRNGKey(d2l.get_seed()) # Generate PRNG keys
M = jax.random.normal(get_key(), (4, 4))
print('a single matrix n', M)
for i in range(100):
M = jnp.matmul(M, jax.random.normal(get_key(), (4, 4)))
print('after multiplying 100 matricesn', M)
a single matrix [[-1.531857 -1.6248469 -1.7896363 0.01071274] [-0.83422506 -1.583117 -0.04581776 -0.6887173 ] [ 0.5935193 -1.4750035 0.5265016 -1.0061077 ] [-0.6028679 -0.3464505 1.1737709 -1.3659075 ]] after multiplying 100 matrices [[-2.7093967e+25 6.4777160e+24 -1.1368576e+25 -7.9616848e+25] [ 9.1084851e+24 -2.1776870e+24 3.8219019e+24 2.6765695e+25] [ 2.6918674e+25 -6.4358044e+24 1.1295020e+25 7.9101732e+25] [ 3.1859349e+25 -7.6170382e+24 1.3368117e+25 9.3620141e+25]]
M = tf.random.normal((4, 4))
print('a single matrix n', M)
for i in range(100):
M = tf.matmul(M, tf.random.normal((4, 4)))
print('after multiplying 100 matricesn', M.numpy())
a single matrix tf.Tensor( [[ 0.6401031 -0.30267003 -1.2595664 -0.09789732] [-1.7108601 0.5364894 -0.02595425 0.32053235] [-0.40997565 -0.6582443 -0.7346871 1.9668812 ] [ 0.16821837 -0.41409513 -0.5977446 -0.38071403]], shape=(4, 4), dtype=float32) after multiplying 100 matrices [[1.5536073e+21 5.0625842e+21 2.7629899e+21 3.1974600e+21] [6.6411150e+20 2.1640736e+21 1.1810791e+21 1.3667998e+21] [3.0877614e+21 1.0061778e+22 5.4913826e+21 6.3548842e+21] [3.9506273e+20 1.2873513e+21 7.0259335e+20 8.1307368e+20]]
5.4.1.3. 打破對稱
神經網絡設計中的另一個問題是其參數化中固有的對稱性。假設我們有一個帶有一個隱藏層和兩個單元的簡單 MLP。在這種情況下,我們可以置換權重 W(1)第一層的權重,同樣置換輸出層的權重以獲得相同的函數。第一個隱藏單元與第二個隱藏單元沒有什么特別的區別。換句話說,我們在每一層的隱藏單元之間具有排列對稱性。
這不僅僅是理論上的麻煩。考慮前面提到的具有兩個隱藏單元的單隱藏層 MLP。為了說明,假設輸出層將兩個隱藏單元轉換為僅一個輸出單元。想象一下,如果我們將隱藏層的所有參數初始化為 W(1)=c對于一些常數c. 在這種情況下,在前向傳播過程中,任一隱藏單元采用相同的輸入和參數,產生相同的激活,并將其饋送到輸出單元。在反向傳播期間,根據參數區分輸出單元W(1)給出一個梯度,其元素都取相同的值. 因此,在基于梯度的迭代(例如,小批量隨機梯度下降)之后, W(1)仍然取相同的值。這樣的迭代永遠不會自行破壞對稱性,我們可能永遠無法實現網絡的表達能力。隱藏層的行為就好像它只有一個單元。請注意,雖然小批量隨機梯度下降不會破壞這種對稱性,但 dropout 正則化(稍后介紹)會!
5.4.2. 參數初始化
解決或至少減輕上述問題的一種方法是通過仔細初始化。正如我們稍后將看到的,在優化和適當的正則化過程中額外注意可以進一步提高穩定性。
5.4.2.1. 默認初始化
在前面的部分中,例如,在第 3.5 節中,我們使用正態分布來初始化我們的權重值。如果我們不指定初始化方法,框架將使用默認的隨機初始化方法,這在實踐中通常適用于中等規模的問題。
5.4.2.2. 澤維爾初始化
讓我們看一下輸出的尺度分布oi對于一些沒有非線性的完全連接層。和 nin輸入xj及其相關權重 wij對于這一層,輸出由下式給出
(5.4.3)oi=∑j=1ninwijxj.
權重wij都是從同一個分布中獨立抽取的。此外,我們假設此分布的均值和方差為零σ2. 請注意,這并不意味著分布必須是高斯分布,只是意味著均值和方差需要存在。現在,我們假設層的輸入 xj也有零均值和方差γ2并且它們獨立于wij并且相互獨立。在這種情況下,我們可以計算的均值和方差oi如下:
(5.4.4)E[oi]=∑j=1ninE[wijxj]=∑j=1ninE[wij]E[xj]=0,Var[oi]=E[oi2]?(E[oi])2=∑j=1ninE[wij2xj2]?0=∑j=1ninE[wij2]E[xj2]=ninσ2γ2.
保持方差固定的一種方法是設置 ninσ2=1. 現在考慮反向傳播。我們面臨著類似的問題,盡管梯度是從更靠近輸出的層傳播的。使用與前向傳播相同的推理,我們看到梯度的方差會爆炸,除非 noutσ2=1, 在哪里nout是這一層的輸出個數。這讓我們進退兩難:我們不可能同時滿足這兩個條件。相反,我們只是嘗試滿足:
(5.4.5)12(nin+nout)σ2=1or equivalentlyσ=2nin+nout.
這就是現在標準且實際有益的Xavier 初始化背后的推理,以其創建者的第一作者命名(Glorot 和 Bengio,2010)。通常,Xavier 初始化從具有零均值和方差的高斯分布中采樣權重 σ2=2nin+nout. 當從均勻分布中采樣權重時,我們也可以調整它來選擇方差。注意均勻分布U(?a,a)有方差a23. 堵漏a23進入我們的條件σ2產生根據初始化的建議
(5.4.6)U(?6nin+nout,6nin+nout).
盡管在神經網絡中很容易違反上述數學推理中不存在非線性的假設,但 Xavier 初始化方法在實踐中表現良好。
5.4.2.3. 超過
上面的推理僅僅觸及了現代參數初始化方法的皮毛。深度學習框架通常會實施十幾種不同的啟發式方法。此外,參數初始化仍然是深度學習基礎研究的熱點領域。其中包括專門用于綁定(共享)參數、超分辨率、序列模型和其他情況的啟發式方法。例如, 肖等人。( 2018 )通過使用精心設計的初始化方法證明了在沒有架構技巧的情況下訓練 10000 層神經網絡的可能性。
如果您對該主題感興趣,我們建議您深入研究該模塊的內容,閱讀提出和分析每個啟發式的論文,然后探索有關該主題的最新出版物。也許您會偶然發現甚至發明一個聰明的想法并為深度學習框架貢獻一個實現。
5.4.3. 概括
梯度消失和爆炸是深度網絡中的常見問題。需要非常小心地進行參數初始化,以確保梯度和參數得到很好的控制。需要初始化啟發式方法來確保初始梯度既不過大也不過小。隨機初始化是確保優化前對稱性被破壞的關鍵。Xavier 初始化表明,對于每一層,任何輸出的方差都不受輸入數量的影響,并且任何梯度的方差都不受輸出數量的影響。ReLU 激活函數減輕了梯度消失問題。這可以加速收斂。
5.4.4. 練習
除了 MLP 層中的置換對稱性之外,您能否設計神經網絡可能表現出需要破壞的對稱性的其他情況?
我們能否將線性回歸或 softmax 回歸中的所有權重參數初始化為相同的值?
查找兩個矩陣乘積的特征值的解析界限。這告訴您有關確保梯度條件良好的什么信息?
如果我們知道某些術語存在分歧,我們能否在事后解決這個問題?查看有關分層自適應速率縮放的論文以獲取靈感 (You等人,2017 年)。
-
pytorch
+關注
關注
2文章
809瀏覽量
13758
發布評論請先 登錄
字符型、指針型等變量該如何初始化
產品程序運行穩定性問題:假如HSE初始化失敗,需要做哪些事情?
手機模塊初始化向導
電感的穩定性
電力系統暫態穩定性快速數值計算方法
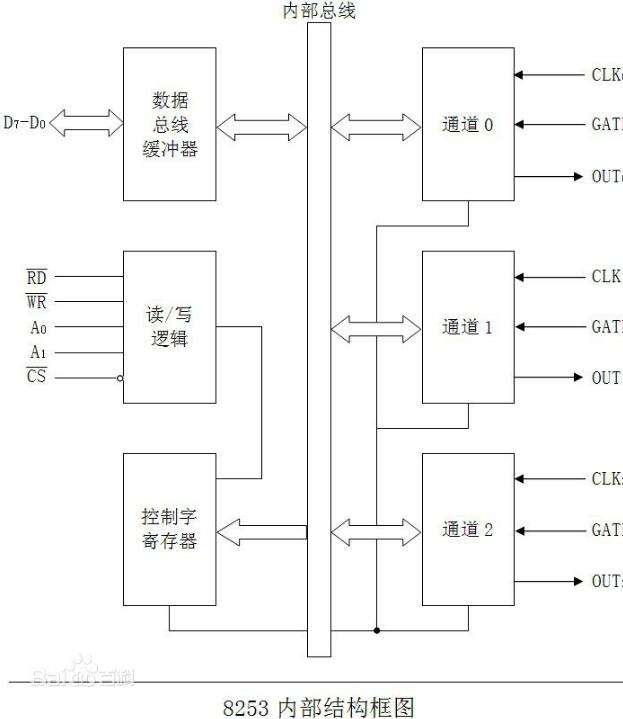
8253初始化程序分享_8253應用案例
在51平臺下初始化文件的引入導致全局變量無法初始化的問題如何解決

怎么分析電路的穩定性?
STM32F407 MCU使用SD NAND?不斷電初始化失效解決方案






 PyTorch教程-5.4. 數值穩定性和初始化
PyTorch教程-5.4. 數值穩定性和初始化












評論