紐結(jié)理論（knot theory）已經(jīng)超越了抽象的數(shù)學(xué)好奇心，推動了數(shù)學(xué)及其他領(lǐng)域的許多發(fā)現(xiàn)。

紐結(jié)理論最初是為了理解宇宙的基本構(gòu)成。1867年，當(dāng)科學(xué)家們急切地試圖找出可以解釋所有不同種類物質(zhì)的方法時，蘇格蘭數(shù)學(xué)家和物理學(xué)家彼得·格思里·泰特（Peter Guthrie Tait）向他的朋友和同胞威廉·湯姆森爵士（Sir William Thomson）展示了他用于產(chǎn)生煙圈的設(shè)備。湯姆森——后來成為開爾文勛爵（與熱力學(xué)溫標(biāo)同名）——被環(huán)迷人的形狀、穩(wěn)定性和相互作用所吸引。他的靈感將他引向了一個令人驚訝的方向：也許，他想，就像煙圈是空氣中的漩渦一樣，原子是發(fā)光以太中結(jié)成紐結(jié)的渦旋環(huán)，物理學(xué)家曾認(rèn)為，光通過以太這種無形介質(zhì)傳播。

雖然這個維多利亞時代的想法現(xiàn)在聽起來可能很荒謬，但這并不是一個輕率的研究。這個漩渦理論有很多值得借鑒的地方：紐結(jié)的多樣性，每個紐結(jié)略有不同，似乎反映了許多化學(xué)元素的不同性質(zhì)。渦旋環(huán)的穩(wěn)定性也可能提供原子所需的持久性。

渦旋理論在科學(xué)界獲得了關(guān)注，并激發(fā)了泰特開始將所有紐結(jié)制成表格，創(chuàng)造了他希望等同于元素周期表的東西。當(dāng)然，原子不是紐結(jié)，也沒有以太。到1880年代后期，湯姆森逐漸放棄了他的渦旋理論，但那時泰特被他的紐結(jié)的數(shù)學(xué)優(yōu)雅所吸引，他繼續(xù)他的制表項目。在這個過程中，他建立了紐結(jié)理論的數(shù)學(xué)領(lǐng)域。

我們都熟悉紐結(jié)——它們讓我們的腳能穿上鞋，讓船固定在碼頭上，讓登山者能從下面的巖石上來。但這些紐結(jié)并不完全是數(shù)學(xué)家（包括泰特）所說的紐結(jié)。雖然纏繞起來的線團可能看起來打了結(jié)，但總是可以解開它。要打一個數(shù)學(xué)紐結(jié)，你必須將線的自由末端插在一起以形成一個閉環(huán)。

因為紐結(jié)像繩子（或譯為弦）一樣靈活，數(shù)學(xué)家將紐結(jié)理論視為拓撲學(xué)的一個子領(lǐng)域，即對可延展形狀的研究。有時可以解開一個紐結(jié)，讓它變成一個簡單的圓，我們稱之為“（可）解紐結(jié)”（unknot）。但更多時候，解開一個紐結(jié)是不可能的。

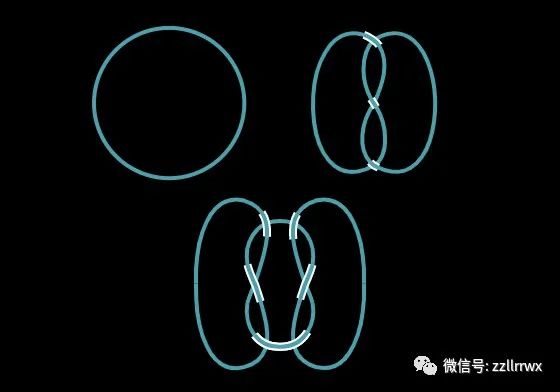
三個簡單的紐結(jié)（從左上角順時針方向）：（可）解紐結(jié)、三葉紐結(jié)（trefoil）和方形紐結(jié)。

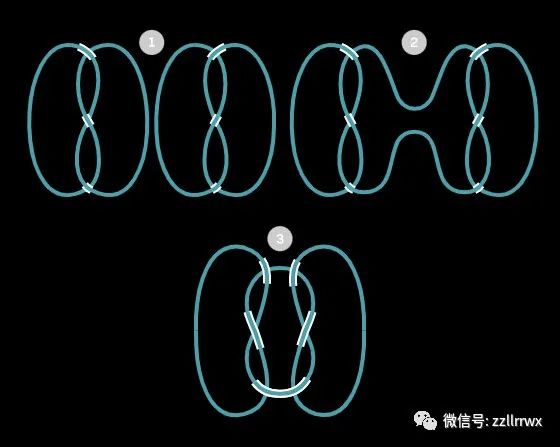
紐結(jié)也可以組合形成新的紐結(jié)。例如，將稱為三葉草的簡單紐結(jié)與其鏡像結(jié)合會產(chǎn)生一個方形紐結(jié)。（如果你加入兩個相同的三葉紐結(jié)，你就得到一個奶奶紐結(jié)（granny knot）。

?

將三葉紐結(jié)及其鏡像連接起來，形成一個方形紐結(jié)。 使用數(shù)字世界的術(shù)語，數(shù)學(xué)家說三葉紐結(jié)是素紐結(jié)，方紐結(jié)是（復(fù)合、合成）合紐結(jié)，（可）解紐結(jié)既不是素的，也不是合的（就與數(shù)字1一樣，既不是素數(shù)，也不是合數(shù)）。這個類比在1949年得到了進一步的支持，當(dāng)時霍斯特·舒伯特（Horst Schubert）證明了每個紐結(jié)要么是素紐結(jié)，要么可以唯一地分解為素紐結(jié)。

創(chuàng)建新紐結(jié)的另一種方法是將兩個或多個紐結(jié)交織在一起，形成一個鏈。波羅密歐環(huán)（Borromean ring）之所以如此命名，是因為它們出現(xiàn)在意大利Borromeo波羅密歐家族的徽章上，它就是一個簡單的例子。

?

為了形成Borromean環(huán)，三個環(huán)必須相互連接，而沒有兩個單獨的圓環(huán)相連。

湯姆森和泰特并不是第一個以數(shù)學(xué)方式看待紐結(jié)的人。早在1794年，卡爾·弗里德里希·高斯（Carl Friedrich Gauss）就在他的個人筆記本上寫下并畫了紐結(jié)的例子。高斯的學(xué)生約翰·利斯廷（Johann Listing）在他1847年的專著《拓撲學(xué)的初步研究》（Vorstudien zur Topologie）中寫到了紐結(jié)——這也是拓撲學(xué)一詞的起源。

但泰特是第一個研究紐結(jié)理論基本問題的學(xué)者：所有可能的紐結(jié)的分類和制表。通過多年的艱苦工作，僅使用他的幾何直覺，他就發(fā)現(xiàn)并對所有素紐結(jié)進行了分類，當(dāng)投影到平面上時，最多有七個交叉點。

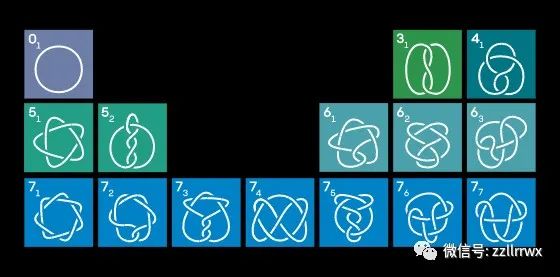
以元素周期表的樣式排列的可解紐結(jié)和所有具有七個或更少交叉（忽略鏡像）的素紐結(jié)。

在19世紀(jì)末，泰特得知另外兩個人——托馬斯·柯克曼牧師（Rev. Thomas Kirkman）和美國數(shù)學(xué)家查爾斯·利特爾（Charles Little）——也在研究這個問題。在他們的共同努力下，他們將所有素紐結(jié)分類為多達 10 個交叉點，其中許多具有 11 個交叉點。令人驚訝的是，他們10個及10個以內(nèi)交叉點的紐結(jié)表是完整的：沒有錯過任何紐結(jié)。

值得注意的是，泰特、柯克曼和利特爾在沒有后來幾年中發(fā)現(xiàn)的定理和技術(shù)的情況下取得了如此多的成就。但對他們有利的一件事是，大多數(shù)小紐結(jié)都是“交替的”，這意味著它們有一個投影，其中交叉點表現(xiàn)出一致的上-下-上-下模式。

交替紐結(jié)具有比非交替紐結(jié)更容易分類的特性。例如，很難找到任何紐結(jié)投影的最小交叉數(shù)。但是泰特多年來錯誤地認(rèn)為所有的紐結(jié)都是交替的，他推測了一種判斷是否找到最小數(shù)字的方法：如果一個交替投影沒有可以通過翻轉(zhuǎn)部分紐結(jié)即可消除的交叉點，那么它一定是交叉次數(shù)最少的投影。

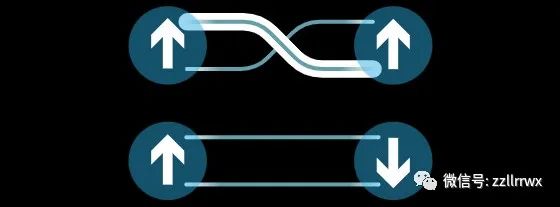
特稱任何可以通過翻轉(zhuǎn)部分紐結(jié)來消除的交叉點都是“無價值的”（nugatory）或無關(guān)緊要的。

泰特關(guān)于交替紐結(jié)的另外兩個猜想最終都是真的。然而，這些著名的猜想直到1980年代末和90年代初，使用沃恩·瓊斯（Vaughan Jones）于1984年開發(fā)的數(shù)學(xué)工具后，才被證明。瓊斯因在紐結(jié)理論方面的工作而獲得菲爾茲獎。

不幸的是，交替的紐結(jié)只能帶你走這么遠。一旦我們進入有八個或更多交叉的紐結(jié)，非交替紐結(jié)的數(shù)量就會迅速增加，這使得泰特的技術(shù)變得不那么有用。

這個8-交叉紐結(jié)，作為真愛之人的紐結(jié)，不能用交替的投影來繪制。

所有 10-交叉紐結(jié)的原始表是完整的，但泰特、柯克曼和利特爾重復(fù)計算了。直到1970年代，曾在普林斯頓大學(xué)研究紐結(jié)理論的律師肯尼斯·佩爾科（Kenneth Perko）才注意到其中兩個紐結(jié)是彼此的鏡像。為了紀(jì)念他，他們現(xiàn)在被稱為Perko對（Perko pair）。

這兩個 10-交叉紐結(jié)，稱為 Perko 對，是同一個紐結(jié)。

在過去的一個世紀(jì)里，數(shù)學(xué)家們發(fā)現(xiàn)了許多聰明的方法來確定紐結(jié)是否真的不同。從本質(zhì)上講，這個想法是識別一個不變量——與節(jié)點相關(guān)的屬性、數(shù)量或代數(shù)實體，通常可以簡單地計算。（這些屬性具有可著色性（colorability）、橋數(shù)（bridge number）或 翻滾（writhe） 等名稱。有了這些標(biāo)簽，數(shù)學(xué)家現(xiàn)在可以很容易地比較兩個紐結(jié)：如果它們在任何給定的屬性上不同，那么它們就不是同一個紐結(jié)。然而，這些性質(zhì)都不是數(shù)學(xué)家所說的完全不變量，這意味著兩個不同的節(jié)點可能具有相同的性質(zhì)。

由于所有這些復(fù)雜性，紐結(jié)的制表仍在進行中也就不足為奇了。最近，在 2020 年，本杰明·伯頓（Benjamin Burton）將所有多達 19 個交叉的素紐結(jié)進行了分類（有近 3 億個） https://drops.dagstuhl.de/opus/volltexte/2020/12183/ 。

傳統(tǒng)的紐結(jié)理論只在三維空間才有意義：在二維中，只有可解紐結(jié)是可能的，而在四維中，額外的空間允許紐結(jié)自行解開，所以每個紐結(jié)都與可解紐結(jié)相同。

然而，在四維空間中，我們可以給球面打結(jié)。為了理解這意味著什么，想象一下以規(guī)則的間隔切割一個普通的球面。這樣做會產(chǎn)生圓圈，就像緯度線一樣。然而，如果我們有一個額外的維度，我們可以把球面打結(jié)，所以這些切片，現(xiàn)在是三維的，而不是二維的，可以成為紐結(jié)。

當(dāng)我們在三維空間中切一個球面時，我們得到的是圓。但是在四維空間中打結(jié)的球面的切片可能是紐結(jié)。

這個想法是紐結(jié)理論最近最大的結(jié)果之一。2018年，當(dāng)時的研究生麗莎·皮奇里洛（Lisa Piccirillo）解決了50年前的問題，即約翰·康威（John Conway）首次發(fā)現(xiàn)的11-交叉紐結(jié)。這個問題與一種叫做sliceness（可切性）的屬性有關(guān)。正如我們所看到的，當(dāng)我們在四維中切開一個打紐結(jié)的球面時，我們會在三維空間中獲得一個紐結(jié)或鏈。有時我們可以從一個漂亮的光滑紐結(jié)球面中獲得給定的紐結(jié)，但對于其他紐結(jié)，球面必須像一張廢紙一樣打結(jié)和皺縮。從本質(zhì)上講，Piccirillo證明了康威的紐結(jié)屬于后一種類型。用技術(shù)術(shù)語來說，她證明了它不是“光滑切片”（smoothly slice）。

Lisa Piccirillo證明，康威紐結(jié)并不“光滑”。

幾個世紀(jì)以來，紐結(jié)理論在數(shù)學(xué)領(lǐng)域縱橫交錯。它最初是數(shù)學(xué)的一個應(yīng)用領(lǐng)域，湯姆森試圖用紐結(jié)來理解物質(zhì)的構(gòu)成。隨著這個想法的消失，它變成了純數(shù)學(xué)的一個領(lǐng)域，是拓撲學(xué)這個有趣且仍然不實用的領(lǐng)域的一個分支。但近年來，紐結(jié)理論再次成為數(shù)學(xué)的一個應(yīng)用領(lǐng)域，因為科學(xué)家利用紐結(jié)理論的思想來研究流體力學(xué)、電動力學(xué)、紐結(jié)分子如DNA等。幸運的是，當(dāng)科學(xué)家們忙于研究其他事情時，數(shù)學(xué)家們正在建立紐結(jié)目錄和解開它們秘密的工具。

審核編輯：劉清