精品无码AV人妻受辱系列,色色色姑娘,2022色老板

為什么我們代碼將浮點數、整數進行強制轉換，或打印輸出時會出精度損失，或出錯的情況？

想要搞明白這個問題，就需要了解一下整數、浮點數的存儲規則。

浮點數存儲規則

根據國際標準IEEE（電氣和電子工程協會）規定，任何一個浮點數NUM的二進制數可以寫為：

NUM = (-1) ^ S * M * 2 ^ E; (S表示符號，E表示階乘，M表示有效數字) ①當S為0時，表示一個正數；當S為1時，表示一個負數； ②M表示有效數字，1<= M <2； ③2^E表示指數比如十進制的3.0，二進制就是0011.0 就可以寫成（-1）^ 0 * 1.1 * 2 ^ 1 再比如十進制的-3.0，二進制就是-0011.0 就可以寫成（-1）^ 1 * 1.1 * 2 ^ 1 而規定float類型有一個符號位（S），有8個指數位（E），和23個有效數字位（M） double類型有一個符號位（S），有11個指數位（E），和52個有效數字位（M）以float類型為例：

IEEE對于（有效數字）M和（指數）E有特殊的規定（以float為例）：1.因為M的值一定是1<= M <2，所以它絕對可以寫成1.xxxxxxx的形式，所以規定M在存儲時舍去第一個1，只存儲小數點之后的數字。這樣做節省了空間，以float類型為例，就可以保存23位小數信息，加上舍去的1就可以用23位來表示24個有效的信息。 2.對于E（指數）E是一個無符號整數所以E的取值范圍為（0~ 255），但是在計數中指數是可以為負的，所以規定在存入E時，在它原本的值上加上中間數（127），在使用時減去中間數（127），這樣E的真正取值范圍就成了（-127~128）。對于E還分為三種情況：①E不全為0，不全為1:這時就用正常的計算規則，E的真實值就是E的字面值減去127（中間值)，M的值要加上最前面的省去的1。②E全為0這時指數E等于1-127為真實值，M不在加上舍去的1，而是還原為0.xxxxxxxx小數。這樣為了表示0，和一些很小的整數。所以在進行浮點數與0的比較時，要注意。③E全為1當M全為0時，表示±無窮大（取決于符號位）；當M不全為1時，表示這數不是一個數（NaN）

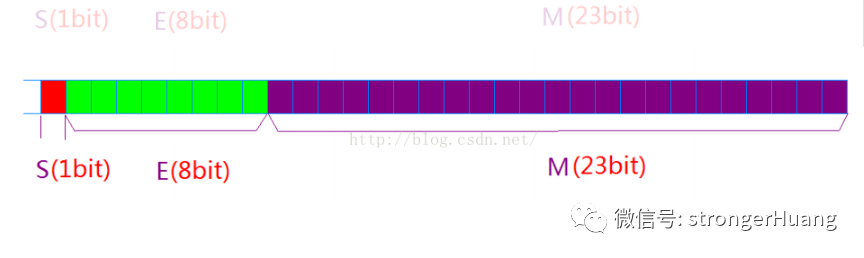
測試

代碼如下：

void test(void){  float m=134.375;  char *a=(char*)&m;
  printf("0x%p:%d
",a,*a);  printf("0x%p:%d
",a+1,*(a+1) );  printf("0x%p:%d
",a+2,*(a+2) );  printf("0x%p:%d
",a+3,*(a+3) );}

代碼輸出結果：

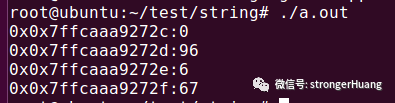
具體的計算過程如下：

精度損失

我們可以把十進制的小數部分乘以2，取整數部分作為二進制的一位，剩余小數繼續乘以2，直至不存在剩余小數為止。例如0.2可以轉換為：0.2 x 2 = 0.4 00.4 x 2 = 0.8 00.8 x 2 = 1.6 10.6 x 2 = 1.2 10.2 x 2 = 0.4 00.4 x 2 = 0.8 00.8 x 2 = 1.6 1… 即：.0011001…它是一個無限循環的二進制數，這就是為什么十進制小數轉換成二進制小數的時候為什么會出現精度損失的情況。 之前前不久給大家分享的《單精度、雙精度、多精度和混合精度計算的區別是什么?》可能大家不是很明白，今天看了浮點數的存儲規則，你明白了嗎？

整數的存儲規則

理解了浮點數的存儲規則，再理解整數就很簡單了。

整數在內存中都是以補碼的形式進行存儲，整數有正負之分。當需存儲有符號數時，用第一位來表示正（0）和負（1）。

正數的反碼和補碼還是它本身，下面主要討論下負數的反碼和補碼。反碼是其原碼除去最高符號位后其余位按位取反，補碼是其反碼在加上1 。

測試代碼：

void test(void){  int8_t n=-123;  uint8_t *p=(uint8_t *)&n;
  printf("%d
",n);  printf("%d
",*p);  }

輸出結果：

計算過程如下：

審核編輯：李倩

聲明：本文內容及配圖由入駐作者撰寫或者入駐合作網站授權轉載。文章觀點僅代表作者本人，不代表電子發燒友網立場。文章及其配圖僅供工程師學習之用，如有內容侵權或者其他違規問題，請聯系本站處理。舉報投訴

二進制

二進制

+關注

關注
2

文章
803

瀏覽量
42154
浮點數

浮點數

+關注

關注
0

文章
61

瀏覽量
16080
代碼

代碼

+關注

關注
30

文章
4887

瀏覽量
70259

原文標題：內存中整數和浮點數存儲的差異

文章出處：【微信號：strongerHuang，微信公眾號：strongerHuang】歡迎添加關注！文章轉載請注明出處。

女人自慰AV免费观看内涵网,日韩国产剧情在线观看网址,神马电影网特片网,最新一级电影欧美,在线观看亚洲欧美日韩,黄色视频在线播放免费观看,ABO涨奶期羡澄,第一导航fulione,美女主播操b

搜索歷史

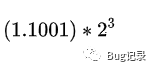
浮點數存儲規則

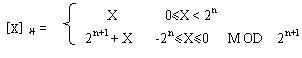
評論