我們每個人從小最先學的數學就是1+1=2,然后就是小九九,因為這是我們長大以后混世界的最基本的能力,加、減、乘、除是人腦“數字邏輯”的基礎。作為替代人腦進行運算的數字計算機,無論是控制器還是處理器,無論是簡單的單片機還是大型的服務器,以加、減法為基礎的算術單元自然是最重要的核心部件。
雖然我們對十進制的加減乘除都已經熟悉到了本能的地步,如何讓晶體管構建的、以二進制為基礎的數字電路來實現我們人類需要的加、減、乘、除?
著名科普專家“冬瓜哥”在其定價為600元的巨著《大話計算機》開篇就對這個問題進行了闡述:
十余年的困惑,自然是上升到了常人不可達的層面才想明白的一些道理,有興趣的同學可以跟著他的思路繞一繞,蘇老師讀了半個小時就已經感覺到腦細胞嚴重疲勞。
他切入計算機的入口就是加法器,準確地講就是在我們的數字電路中一帶而過的Adder - 半加器、全加器以及超前進位加法器(很多教程僅給出了半頁的篇幅)。冬瓜哥得出的結論是“CPU內部就是個加法器”。可見它的重要性,也可見我們對它真的是嚴重忽略了,就像1+1=2一樣,它重要得實在太平凡了。
但,它確實是我們數字計算的基礎,理解了它才能夠理解整個的數字邏輯世界。
我們先通過硬禾學堂制作的一個7分鐘的視頻教程來看一下加法器最基本的兩個示例:
第一個案例 - 1位半加器
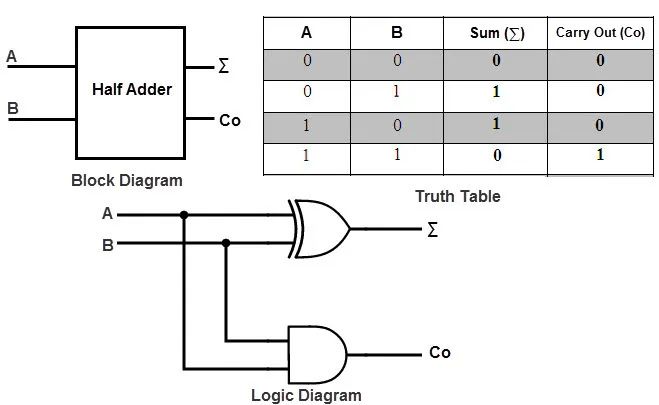
根據我們人類在十進制領域定義的加法規則,來操作2個1位的數據相加,從最基本的門的功能以及加法的規則需求,我們得到來實現它的電路 - 通過一個“異或門”得到加法以后的1位的結果,以及通過一個“與門”得到一個“進位”位的值,就像我們十進制的加法,如果兩個數字相加超過了一個“位”(十進制的位)能夠表達的范圍,就要生成一個進位信號。通過真值表能夠比較直觀地看出反映2個輸入位同經過加法操作以后得到的輸出位的關系。
使用Verilog代碼的1位半加器:
module halfadder ( input a, //第一個加數a input b, //第二個加數b output sum, //顯示和的led output cout //顯示進位的led ); assign sum=a ^ b; //sum=a⊕b assign cout=a & b; //cout=ab endmodule
第二個案例 - 1位全加器
畢竟2個1位的數相加只是基礎,太局限,我們擴展一下,如果需要有超過1位的數字相加,該如何操作?那就需要將“進位”的值考慮進來,作為一個輸入,有了進位輸入、進位輸出的加法器被稱之為“全加器”,全了,誰都不缺了。
使用Verilog代碼的1位全加器的Verilog代碼:
module adder1 ( input wire a, //輸入的低位進位及兩個加數cin、a、b input wire b, input wire cin, output wire sum, //輸出的和與進位 output wire cout ); wire s1,s2,s3; //定義中間變量 xor (s1,a,b); //調用基本異或門 xor (sum,s1,cin); nand (s2,a,b); //調用基本與非門 nand (s3,s1,cin); nand (cout,s2,s3); endmodule
通過上面的兩段Verilog代碼,可以看出用Verilog這種硬件描述語言的一些特點,這個在后面的文章中會專門介紹。
多數的“數字電路”教程關于加法器也基本上點到此為止了。
但上述的基本單元能用來做啥的?如果不做擴展,同學們很難有進一步的理解,因此我建議大家可以自行做一些擴展:
支持多位二進制數相加的并行二進制加法器
比如2個4位二進制的加法器,它可以由3個全加器和1個半加器構成,低位的加法進位可以作為相鄰高位加法的一個輸入端,最低位僅用一個半加器,最高位生成的進位信號作為后續電路的輸入。
是不是像極了我們的十進制加法?原理是一樣的,只是采用的進制不同,而二進制可以通過數字電路的0、1比較容易地實現。
了解了加法器,減法器也就不難理解,就像我們十進制中的加和減的關系一樣。它的基本規則:
0 - 0 = 0
0 - 1 = (借)1 1
1 - 0 = 1
1 - 1 = 0
既然多位的全減器也可以用全加器來實現,是不是可以有一種統一的結構能夠實現加、減的功能?畢竟減和加是對偶的,減法也可以看作是+(-)的操作。
統一結構的并行加、減法
從前面的加減法構成可以看出,加法器和減法器都可以用共同的加法器來實現,如果我們添加一個控制信號M,最低位也使用一個全加器,將這個M值連接到該全加器的進位輸入端,就可以通過這個M是0或1來決定此電路時加法電路還是減法電路:
M=1的時候為減法器
M=0的時候行使加法器的功能。
如果你需要將更多的位數的二進制數字相加或相減,你可以使用更多個加法器級聯即可得到。細心和動腦的同學會發現,如果任何操作需要哪怕一丁點的時間(有了時間的概念也就意味著 - 因果之間有了先后,有了“時延”,我們生存的世界時間是一個客觀存在的維度),那么圖中的操作在每個位上的輸出就會產生時間上的差異,最高位的值和進位依賴于低位的值和每一位加法操作的時間(也就是構成加法器的門的響應時間)。就像綠燈亮起,并不是所有等待的車同時啟動前行,而是從第一輛車逐級傳遞過來的一樣。
用上述方法構建的加法器、減法器,位數越多,由于電路門時延帶來的計算結果會越慢出現,聰明的前輩大神們竟然通過一系列的邏輯運算發明了“超前進位加法器”的結構,即便實際的電路上每個操作都有先后帶來的時延,我們也可以不需要考慮每個進位的逐級傳遞,而是一次性地根據各個輸入端的位上的值直接得出運算以后的結果。
是不是很不可思議?
為啥需要逐級傳遞的信息可以提前預知?為什么在布爾表達式中的一些變量經過邏輯化簡以后發現它們只是打醬油的可有可無?
我們的生活中是否也是如此?每當綠燈亮起的時候所有的車是否也能同步啟動前行?
這些問題留給大家思考。
有了加法器、減法器,也就很容易構建乘法器 - 重復多次的加,和除法器 - 重復多次的減。
因此加法器是構成整個數字計算的基礎,是最重要的一個部件,它的設計好壞直接影響了處理器/控制器的性能、性價比等。
比如在電子森林“電路仿真”中的Brent-Kung樹形加法器就是一種最小化芯片面積和成本的結構。有興趣的同學可以點擊https://www.eetree.cn/war/circuitjs.html?lang=zh 來體驗一下。
正如前面文章所述,在FPGA沒有大面積普及應用的年代,曾經有一系列的中等規模的集成電路模塊推出,最著名的就是74系列的器件,其中74HC283就是一種4位超前進位的全加器器件。很多高校可能還在拿它做數電的實驗,
外形長這樣
內部功能這樣
最后,給大家介紹一款國外公司制作的4位加法器的訓練套件
為了方便大家實驗,這個產品中包含了如下的一些器件:
1個多路選擇器(CD74HC157E)
2個寄存器 /4個D觸發器 (CD74HC173E)
1個4位全加器 (CD74HC283E)
1個6通道具有施密特觸發器輸入的反相器 (CD74HC14E)
1個4位幅度比較器 (CD74HC85E)
1個雙4輸入異或門 (CD74HC4002E)
1個4組 2輸入異或門 (CD74HC86E)
得說,這個套件的文檔寫得特別的棒,有興趣的老師和同學可以自己搜一下。
這個套件用了8顆中等規模的集成電路,加上很多連線連線。其實呢,用小腳丫FPGA內部的不到1%的資源就能實現,而且只需要寫很短的幾行Verilog代碼。
責任編輯:haq
-
處理器
+關注
關注
68文章
19813瀏覽量
233613 -
電路圖
+關注
關注
10402文章
10732瀏覽量
540896 -
計算機
+關注
關注
19文章
7632瀏覽量
90219
原文標題:淺談“數字電路”的學習(7)- 一切數字計算的核心功能、被教程忽略的加法器
文章出處:【微信號:xiaojiaoyafpga,微信公眾號:電子森林】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
EE-256:使用ADSP-BF561 Blackfin處理器作為TFT-LCD控制器






 控制器和處理器離不開的加法器
控制器和處理器離不開的加法器










評論