寫在前面 Ⅰ
前面寫了關(guān)于ADC采集電壓的文章,大家除了求平均的方式來處理采樣值,還有沒有使用到其他的方式來處理采集值呢?
在某些情況下就需要對一組數(shù)據(jù)進(jìn)行排序,并提取頭特定的數(shù)據(jù)出來使用。
排序的應(yīng)用場合很多,我這里就不再一一舉例說明,掌握排序的基本算法,到時(shí)候遇到就有用武之地。
排序算法分類 Ⅱ
1.按存儲分類:內(nèi)部排序和外部排序
內(nèi)部排序:是數(shù)據(jù)記錄在內(nèi)存中進(jìn)行排序;
外部排序:是因排序的數(shù)據(jù)很大,一般一次不能容納全部的排序記錄,在排序過程中需要訪問外存。
內(nèi)部排序高速、有效,是我們比較常用的排序方法。外部排序速度慢,效率低,一般不建議使用外部排序,比較實(shí)用的排序還是只有內(nèi)部排序。
2.內(nèi)部排序分類:插入排序、選擇排序、交換排序、歸并排序、基數(shù)排序。
排序的分類大致為如下圖:
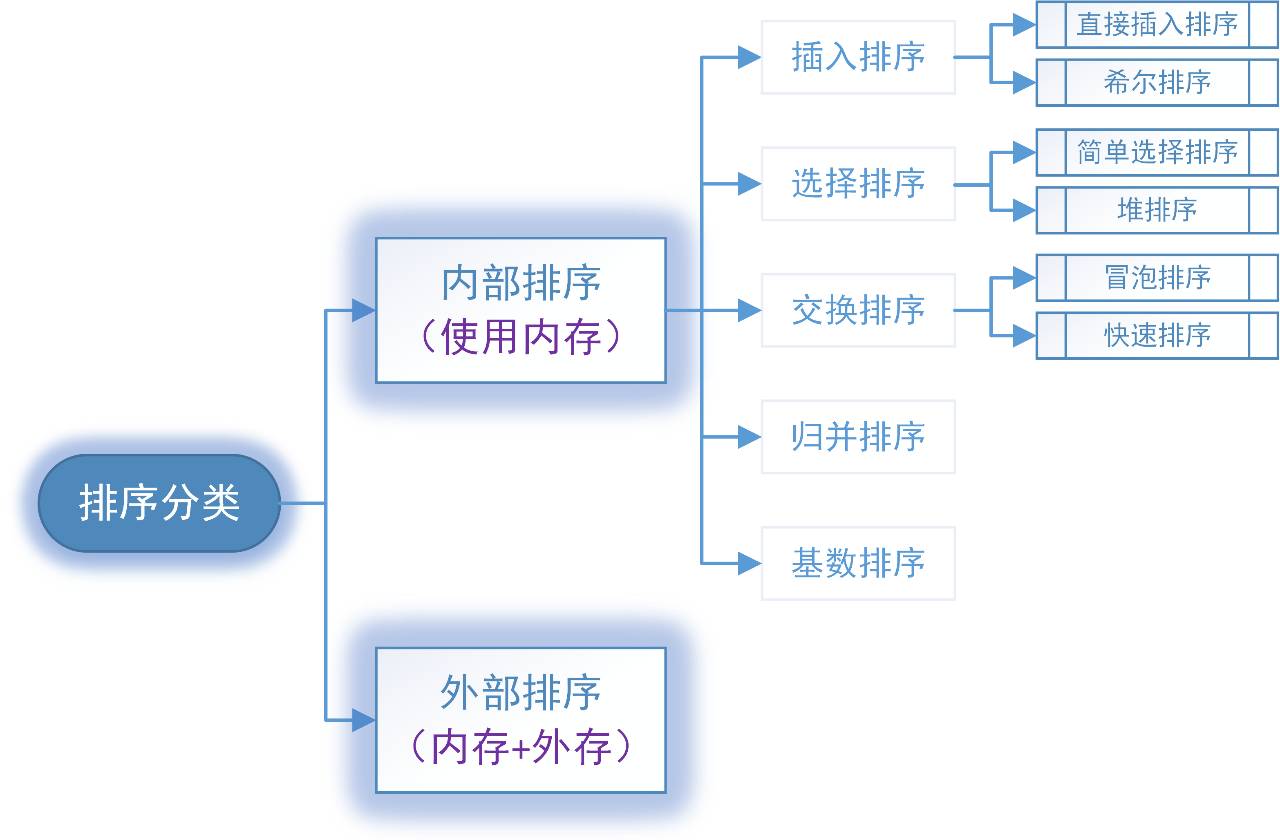
在內(nèi)部排序中,最常見、有效且實(shí)用的排序算是交換排序,本文將在下面章節(jié)重點(diǎn)講述交換排序中的冒泡排序和快速排序。
交換排序 Ⅲ
1.冒泡排序
冒牌排序是我們讀書時(shí)最先接觸的一種排序算法,也是比較經(jīng)典的排序算法。
冒泡排序就是在要排序的一組數(shù)中,對當(dāng)前還未排好序范圍內(nèi)的全部數(shù),自上而下對相鄰的兩個(gè)數(shù)依次進(jìn)行比較和調(diào)整,讓較大的數(shù)往下沉,較小的往上冒。即:每當(dāng)兩相鄰的數(shù)比較后發(fā)現(xiàn)它們的排序與排序要求相反時(shí),就將它們互換。
原始的冒泡排序函數(shù):
void bubbleSort(int a[], int n)
{
for(int i =0 ; i< n-1; ++i)
{
for(int j = 0; j < n-i-1; ++j)
{
if(a[j] > a[j+1])
{
int tmp = a[j];
a[j] = a[j+1];
a[j+1] = tmp;
}
}
}
}
其實(shí),原始的冒泡排序不是最后的算法,如果進(jìn)行某一趟排序時(shí)并沒有進(jìn)行數(shù)據(jù)交換,則說明數(shù)據(jù)已經(jīng)按要求排列好,可立即結(jié)束排序,避免不必要的比較過程。
對冒泡排序常見的改進(jìn)方法是加入標(biāo)志性變量,用于標(biāo)志某一趟排序過程中是否有數(shù)據(jù)交換。
第1種改進(jìn)法:設(shè)置一標(biāo)志性變量pos,用于記錄每趟排序中最后一次進(jìn)行交換的位置。由于pos位置之后的記錄均已交換到位,故在進(jìn)行下一趟排序時(shí)只要掃描到pos位置即可。
void Bubble_1( int r[], int n)
{
int pos = 0;
int i;
int j;
int tmp;
i = n - 1;
while(i > 0)
{
for(j=0; j
{
if(r[j] > r[j+1])
{
pos = j; //記錄交換的位置
tmp = r[j];
r[j] = r[j+1];
r[j+1] = tmp;
}
}
i= pos;
}
}
第2種改進(jìn)法:傳統(tǒng)冒泡排序中每一趟排序操作只能找到一個(gè)最大值或最小值,我們考慮利用在每趟排序中進(jìn)行正向和反向兩遍冒泡的方法一次可以得到兩個(gè)最終值(最大者和最小者) , 從而使排序趟數(shù)幾乎減少了一半。
void Bubble_2(int r[], int n)
{
int low = 0;
int high= n -1;
int tmp,j;
while(low < high)
{
for(j=low; j//正向冒泡,找到最大者
{
if(r[j]> r[j+1])
{
tmp = r[j];
r[j]=r[j+1];
r[j+1]=tmp;
}
--high;
for(j=high; j>low; --j)//反向冒泡,找到最小者
{
if(r[j]
{
tmp = r[j];
r[j]=r[j-1];
r[j-1]=tmp;
}
++low;
}
}
}
}
2.快速排序
大致步驟如下:
1)選擇一個(gè)基準(zhǔn)元素,通常選擇第一個(gè)元素或者最后一個(gè)元素。
2)通過一趟排序?qū)⒋判虻挠涗浄指畛瑟?dú)立的兩部分,其中一部分記錄的元素值均比基準(zhǔn)元素值小。另一部分記錄的元素值比基準(zhǔn)值大。
3)此時(shí)基準(zhǔn)元素在其排好序后的正確位置。
4)然后分別對這兩部分記錄用同樣的方法繼續(xù)進(jìn)行排序,直到整個(gè)序列有序。
舉例:
對無序數(shù)組[6 2 4 1 5 9]排序:
a),先把第一項(xiàng)[6]取出來,
用[6]依次與其余項(xiàng)進(jìn)行比較:
如果比[6]小就放[6]前邊,2 4 1 5都比[6]小,所以全部放到[6]前邊;
如果比[6]大就放[6]后邊,9比[6]大,放到[6]后邊;
一趟排完后變成下邊這樣:
排序前62 4 1 5 9
排序后 2 4 1 569
b),對前半邊[2 4 1 5]繼續(xù)進(jìn)行快速排序
重復(fù)步驟a)后變成下邊這樣:
排序前24 1 5
排序后 124 5
前半邊排序完成,總的排序也完成:
排序前:[6 2 4 1 5 9]
排序后:[1 2 4 5 6 9]
排序結(jié)束
代碼
將前后分開函數(shù):
int partition(int unsorted[], int low, int high)
{
int pivot = unsorted[low];
while(low < high)
{
while((low < high) && (unsorted[high] >= pivot))
--high;
unsorted[low] = unsorted[high];
while((low < high) && (unsorted[low] <= pivot))
++low;
unsorted[high] = unsorted[low];
}
unsorted[low] = pivot;
return low;
}
快速排序函數(shù):
void quickSort(int unsorted[], int low, int high)
{
int loc = 0;
if(low < high)
{
loc = partition(unsorted, low, high);
quickSort(unsorted, low, loc -1);
quickSort(unsorted, loc + 1, high);
}
}
舉例測試:
void Main(void)
{
int i;
int a[6] = {6, 2, 4, 1, 5, 9};
quickSort(a, 0, 5);
for(i=0; i<6; i++)
printf("a[%d] = a[%d]\n", i, a[i]);
}
在排序算法中,這兩種是較重要的排序算法,其他算法在特定場合也有用武之地,本文暫時(shí)講述到這里。
-
adc
+關(guān)注
關(guān)注
99文章
6636瀏覽量
548236 -
排序
+關(guān)注
關(guān)注
0文章
32瀏覽量
9819
發(fā)布評論請先 登錄
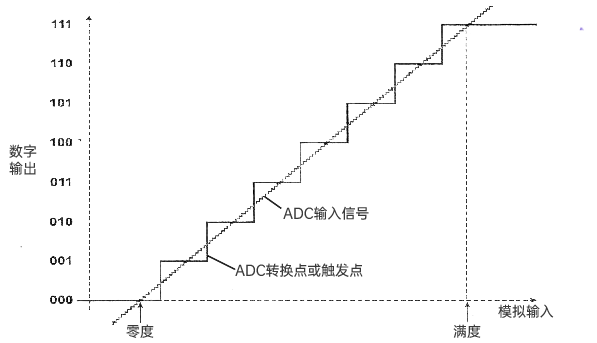
技術(shù)干貨 德思特ADC/DAC靜態(tài)參數(shù)分析系列(一)——什么是ADC轉(zhuǎn)換點(diǎn)?
低成本電源排序器解決方案
UCD9224 2 MHz、2 軌、4 相數(shù)字 PWM 降壓控制器,具有改進(jìn)的排序功能技術(shù)資料

TPS74701-Q1 具有電源正常功能的汽車類 500mA、低 VIN (0.8V)、可調(diào)超低壓差穩(wěn)壓器數(shù)據(jù)手冊

詳解Linux sort命令之掌握排序技巧與實(shí)用案例
TimSort:一個(gè)在標(biāo)準(zhǔn)函數(shù)庫中廣泛使用的排序算法
dp接口的最新技術(shù)發(fā)展
時(shí)間復(fù)雜度為 O(n^2) 的排序算法






 實(shí)用的排序算法 - 交換排序
實(shí)用的排序算法 - 交換排序












評論