電化學交流阻抗譜圖
? ? ? 交流阻抗發式電化學測試技術中一類十分重要的方法,是研究電極過程動力學和表面現象的重要手段。特別是近年來,由于頻率響應分析儀的快速發展,交流阻抗的測試精度越來越高,超低頻信號阻抗譜也具有良好的重現性,再加上計算機技術的進步,對阻抗譜解析的自動化程度越來越高,這就使我們能更好的理解電極表面雙電層結構,活化鈍化膜轉換,孔蝕的誘發、發展、終止以及活性物質的吸脫附過程。
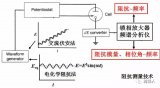
交流阻抗譜檢測方法是給被測體系施加一個小振幅的單正弦波擾動,或者是不同頻率正弦波的疊加,一般是正弦波形式的電壓或者是電流,結果產生相應的電流或電壓的響應信號。
如圖2上圖電流電壓曲線所示,在體系直流電壓E。的條件下外加正弦波電壓Esin(ωt)(ω為角頻率),那么在直流電流I0的基礎上就會得到一個正弦波電流I=sin(ωt+Ф)。得到的電流響應值I受外加電壓E控制。根據歐姆定律Z(ω)=E(ω)/I(ω)可計算出在某個頻率下體系的阻抗值z。

在電化學阻抗技術中,z被定義為一個復數,即Z(ω)=Zre(ω)+jZim(ω),Z2=Zre2+Zim2。其中實部 Zre=∣ Z∣cosθ,虛部Zim=∣Z∣Sinθ相位角θ=tan-1(Zim/Zre)。
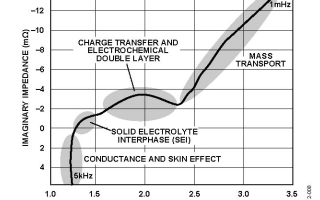
以Zre對Zim作圖,稱為Nyquist圖譜(如圖2下圖左圖譜所示),可以清晰地給出實部和虛部的數值,并可進行體系定性分析。但它不能給出頻率信息,所以通常要采用其它曲線來補充。
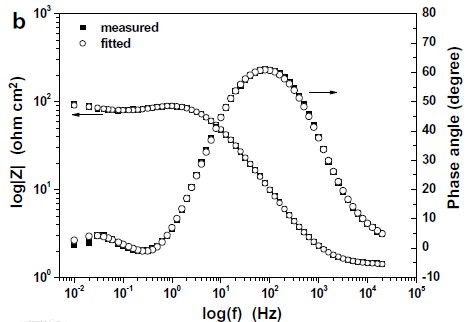
另外一種常用的表示方法是Bode圖,即lgZ、相角對頻率作圖(如圖2下圖右圖譜所示),圖譜中同時表示了阻抗與頻率、相移與頻率的關系。
一般Nyquist圖譜比較普遍,Nyquist圖譜是由一個半圓部分和一個線性部分組成,半圓部分在高頻區,對應的是電子轉移限制過程,半圓越大,電阻就越大,后面直線部分在低頻范圍,對應的是擴散限制過程。
1、阻抗譜中的基本元件
交流阻抗譜的解析一般是通過等效電路來進行的,其中基本的元件包括:純電阻R,純電容C,阻抗值為1/jωC,純電感L,其阻抗值為jωL。實際測量中,將某一頻率為ω的微擾正弦波信號施加到電解池,這是可把雙電層看成一個電容,把電極本身、溶液及電極反應所引起的阻力均視為電阻,則等效電路如圖1所示。
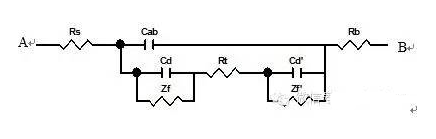
圖1.用大面積惰性電極為輔助電極時電解池的等效電路
圖中A、B分別表示電解池的研究電極和輔助電極兩端,Ra、Rb分別表示電極材料本身的電阻,Cab表示研究電極與輔助電極之間的電容,Cd與Cd’表示研究電極和輔助電極的雙電層電容,Zf與Zf’表示研究電極與輔助電極的交流阻抗。通常稱為電解阻抗或法拉第阻抗,其數值決定于電極動力學參數及測量信號的頻率,Rl表示輔助電極與工作電極之間的溶液電阻。一般將雙電層電容Cd與法拉第阻抗的并聯稱為界面阻抗Z。
實際測量中,電極本身的內阻很小,且輔助電極與工作電極之間的距離較大,故電容Cab一般遠遠小于雙電層電容Cd。如果輔助電極上不發生電化學反映,即Zf’特別大,又使輔助電極的面積遠大于研究電極的面積(例如用大的鉑黑電極),則Cd’很大,其容抗Xcd’比串聯電路中的其他元件小得多,因此輔助電極的界面阻抗可忽略,于是圖1可簡化成圖2,這也是比較常見的等效電路。
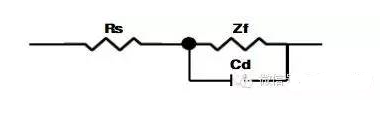
圖2.用大面積惰性電極為輔助電極時電解池的簡化電路
2、阻抗譜中的特殊元件
以上所講的等效電路僅僅為基本電路,實際上,由于電極表面的彌散效應的存在,所測得的雙電層電容不是一個常數,而是隨交流信號的頻率和幅值而發生改變的,一般來講,彌散效應主要與電極表面電流分布有關,在腐蝕電位附近,電極表面上陰、陽極電流并存,當介質中存在緩蝕劑時,電極表面就會為緩蝕劑層所覆蓋,此時,鐵離子只能在局部區域穿透緩蝕劑層形成陽極電流,這樣就導致電流分布極度不均勻,彌散效應系數較低。表現為容抗弧變“癟”,如圖3所示。另外電極表面的粗糙度也能影響彌散效應系數變化,一般電極表面越粗糙,彌散效應系數越低。
2.1、常相位角元件(ConstantPhaseAngleElement,CPE)
在表征彌散效應時,近來提出了一種新的電化學元件CPE,CPE的等效電路解析式為:

角為φ=--pπ/2,由于它的阻抗的數值是角頻率ω的函數,而它的幅角與頻率無關,故文獻上把這種元件稱為常相位角元件。
實際上,當p=1時,如果令T=C,則有Z=1/(jωC),此時CPE相當于一個純電容,波特圖上為一正半圓,相應電流的相位超過電位正好90度,當p=-1時,如果令T=1/L,則有Z=jωL,此時CPE相當于一個純電感,波特圖上為一反置的正半圓,相應電流的相位落后電位正好90度;當p=0時,如果令T=1/R,則Z=R,此時CPE完全是一個電阻。
一般當電極表面存在彌散效應時,CPE-P值總是在1~0.5之間,阻抗波特圖表現為向下旋轉一定角度的半圓圖。
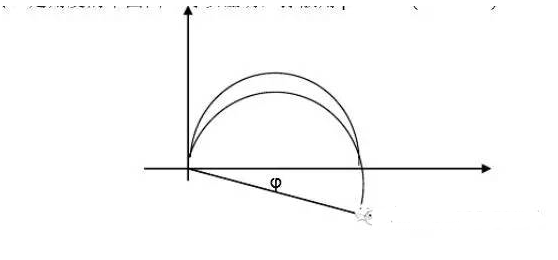
圖3具有彌散效應的阻抗圖
可以證明,彌散角φ=π/2*(1-CPE-P),
特別有意義的是,當CPE-P=0.5時,CPE可以用來取代有限擴散層的Warburg元件,Warburg元件是用來描述電荷通過擴散穿過某一阻擋層時的電極行為。在極低頻率下,帶電荷的離子可以擴散到很深的位置,甚至穿透擴散層,產生一個有限厚度的Warburg元件,如果擴散層足夠厚或者足夠致密,將導致即使在極限低的頻率下,離子也無法穿透,從而形成無限厚度的Warburg元件,而CPE正好可以模擬無限厚度的Warburg元件的高頻部分。當CPE-P=0.5時,

,其阻抗圖為圖3所示,一般在pH》13的堿溶液中,由于生成致密的鈍化膜,阻礙了離子的擴散通道,因此可以觀察到圖4所示的波特圖。
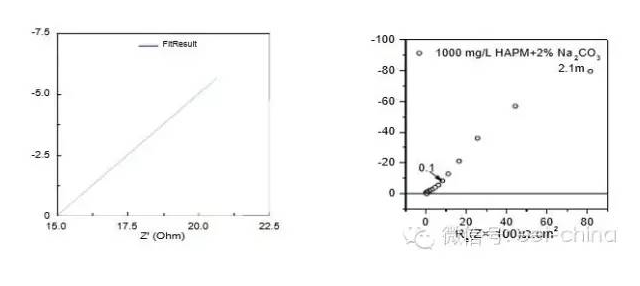
圖4.當CPE-P為0.5時(左)及在Na2CO?3溶液中的波特圖
2.2、有限擴散層的Warburg元件-閉環模型
本元件主要用來解析一維擴散控制的電化學體系,其阻抗為,一般在解析過程中,設置P=0.5,并且Ws-T=L2/D,(其中L是有效擴散層厚度,D是微粒的一維擴散系數),計算表明,當ω-》0時,Z=R,當ω-》+∞,在
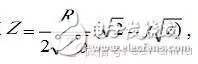
,與CPE-P=0.5時的阻抗表達式相同,阻抗圖如圖5。
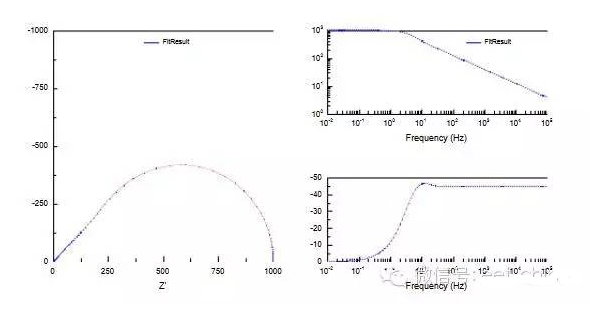
圖5.閉環的半無限的Warburg阻抗圖
2.3、有限擴散層的Warburg元件-發散模型
本元件也是用來描述一維擴散控制的電化學體系,其阻抗為,其中ctnh為反正且函數,F(x)=Ln[(1+x)/(1-x)]。與閉環模型不同的是,其阻抗圖的實部在低頻時并不與實軸相交。而是向虛部方向發散。即在低頻時,更像一個電容。典型的阻抗圖如圖6。
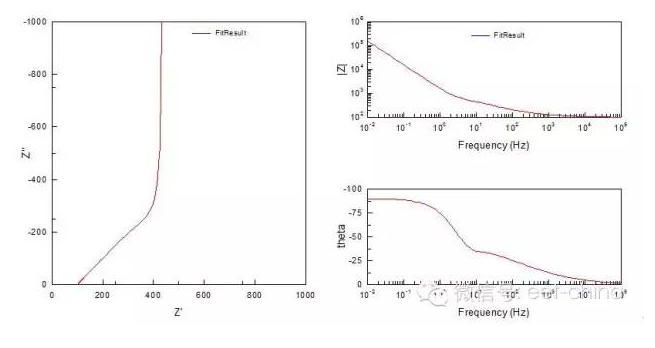
圖6.發散的半無限的Warburg阻抗圖
3、常用的等效電路圖及其阻抗圖譜
對阻抗的解析使一個十分復雜的過程,這不單是一個曲線擬合的問題,事實上,你可以選擇多個等效電路來擬合同一個阻抗圖,而且曲線吻合的相當好,但這就帶來了另外一個問題,哪一個電路符合實際情況呢,這其實也是最關鍵的問題。他需要有相當豐富的電化學知識。需要對所研究體系有比較深刻的認識。而且在復雜的情況下,單純依賴交流阻抗是難以解決問題的,需要輔助以極化曲線以及其它暫態試驗方法。
由于阻抗測量基本是一個暫態測量,所以工作電極,輔助電極以及參比電極的魯金毛細管的位置極有要求。例如魯金毛細管距離參比電極的位置不同,在阻抗圖的高頻部分就會表現出很大的差異,距離遠時,高頻部分僅出現半個容抗弧,距離近時,高頻弧變成一個封閉的弧;當毛細管緊挨著工作電極表面時,可能會出現感抗弧,這其中原因還不清楚。
為了有利于大家在今后的試驗中對阻抗圖有一個粗略的認識,下面簡單將幾種常見阻抗圖譜介紹一下。
3.1、吸附型緩蝕劑體系
如果緩蝕劑不參與電極反應,不產生吸附絡合物等中間產物,則它的阻抗圖僅有一個時間常數,表現為變形的單容抗弧,這是由于緩蝕劑在表面的吸附會使彌散效應增大,同時也使雙電層電容值下降,其阻抗圖及其等效電路如圖7。
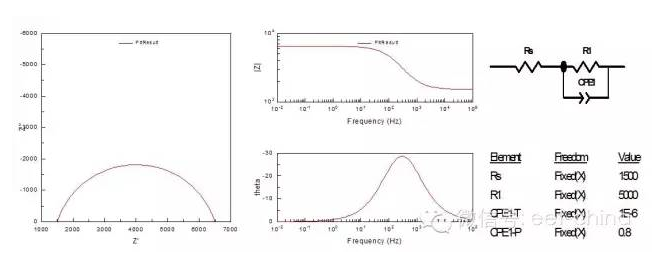
圖7.具有一個時間常數的單容抗弧阻抗圖
3.2、涂層下的金屬電極阻抗圖
涂裝金屬電極存在兩個容性時間常數,一個時涂層本身的電容,另外一個是金屬表面的雙電層電容,阻抗圖上具有雙容抗弧,如圖8所示。
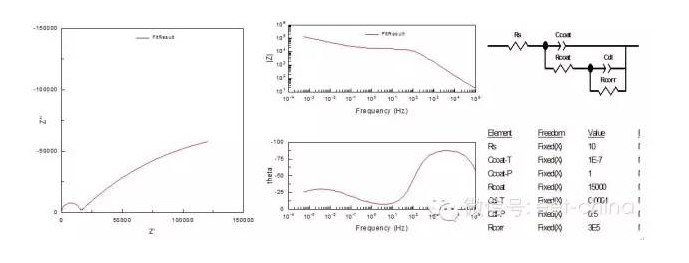
圖8.具有兩個時間常數的涂層金屬阻抗圖
等效電路中的Ccoat為涂層本身的電容,Rcoat為涂層電阻,Cdl為涂層下的雙電層電容,當溶液通過涂層滲透到金屬表面時,還會有電化學反應發生,Rcorr為電極反應的阻抗。
3.3、局部腐蝕的電極阻抗圖
當金屬表面存在局部腐蝕(點腐蝕),點蝕可描述為電阻與電容的串聯電路,其中電阻Rpit為蝕點內溶液電阻,一般Rpit=1~100Ω之間。而是實際體系測得的阻抗應為電極表面鈍化面積與活化面積(即點蝕坑)的界面阻抗的并聯耦合。但因鈍化面積的阻抗遠遠高于活化免得阻抗,因而實際上阻抗頻譜圖反映了電極表面活化面積上的阻抗,即兩個時間常數疊合在一起,表現為一個加寬的容抗弧。其阻抗圖譜與等效電路如圖9所示。
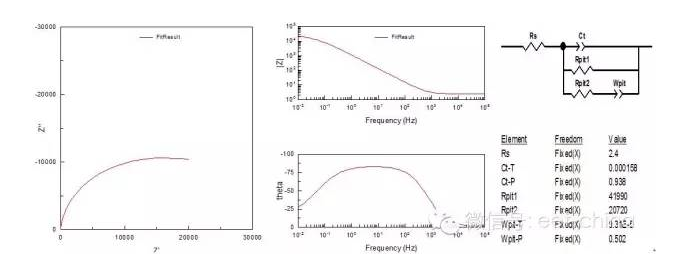
圖9.表面存在局部腐蝕時阻抗圖
3.4、半無限擴散層厚度的電極阻抗圖
所謂半無限擴散過程,是指溶液中的擴散區域,即在定態下擴散粒子的濃度梯度為一定數值的區域,擴散層厚度為無窮大,不過一般如果擴散層厚度大于數厘米后,即可認為滿足這一條件。此時法拉第阻抗就等于半無限擴散控制的濃差極化阻抗Zw與電極反應阻抗Zf的串聯,其阻抗

,電極反應完全受擴散步驟控制,外加的交流信號只會引起表面反應粒子濃度的波動,且電極表面反應粒子的濃度波動相位角正好比交流電流落后45度,阻抗圖為45度角的傾斜直線,如圖10所示。如果法拉第阻抗中有Warburg阻抗,則Rp無窮大,但在腐蝕電位下,由于總的法拉第阻抗是陽極反應阻抗與陰極反應阻抗的并聯,一般僅有陰極反應有Zw,故此時總的Rp應為陽極反應的Rp1值,Zf仍為有限值。
當電極表面存在較厚且致密的鈍化膜時,由于膜電阻很大,離子的遷移過程受到極大的抑制,所以在低頻部分其阻抗譜也表現為一條45度傾角的斜線。
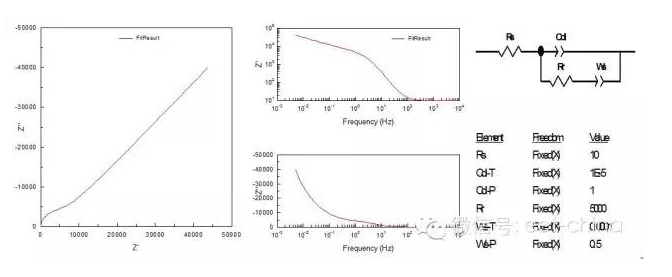
圖10.表面存在致密的鈍化膜時的阻抗圖
3.5、有限擴散層厚度的電極阻抗圖
當擴散層厚度有限時,即在距電極表面l處,擴散粒子的濃度為一不隨時間變化的定值,則有
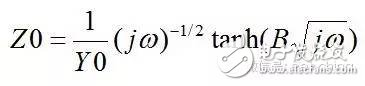
,在低頻是完全由濃差擴散控制,但在高頻使它相當于一個RC串聯電路,見2.2節。實際測量中,當電極表面的存在擴散層控制時,在較低頻率下,離子的遷移過程可以通過延長時間來擴散到金屬表面,發生電化學反應,因此波特圖表現為一閉合的圓弧,可以用有限擴散層厚度的Warburg阻抗來模擬,如圖11所示。
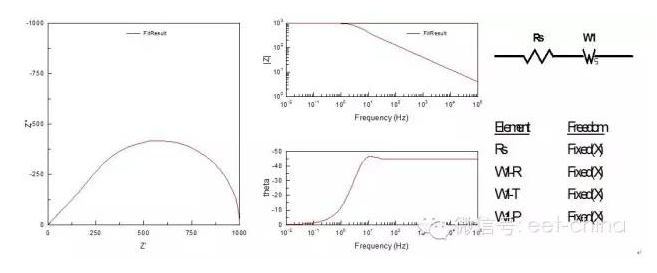
圖11.表面存在非致密的鈍化膜時的阻抗圖
3.6、同時受電化學和濃差極化控制
在混合控制下,交流信號通過電極時,除了濃差極化外還將出現電化學極化,這時電極的法拉第阻抗比較復雜,在高頻部分為雙電層的容抗弧,而在低頻部分,擴散控制將超過電化學控制,出現Warburg阻抗,其等效電路及阻抗圖如圖12所示。
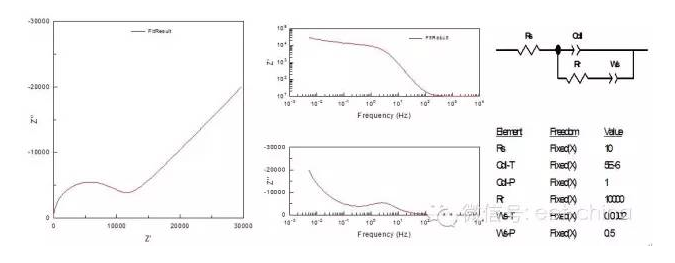
圖12.同時受擴散和電化學控制的阻抗圖
3.7、具有雙容抗弧的電化學阻抗
另外如果法拉第電流If不僅與極化電位?E有關,而且與某一表面狀態變量X相關,則由于X對電位的響應會引起弛豫現象,從而出現除雙電層電容以外的第二個時間常數,不過這第二個時間常數即可能是容性的也可能是感性的,這取決于B值,當B》0時,低頻出現感抗弧,當B《0時,則在低頻出現第二個容抗弧。某些吸附型物質在電極表面成膜后,這層吸附層覆蓋于緊密雙電層之上,且其本身就具有一定的容性阻抗Cf,它與電極表面的雙電層串聯在一起組成具有兩個時間常數的阻抗譜,其阻抗圖如圖13所示。
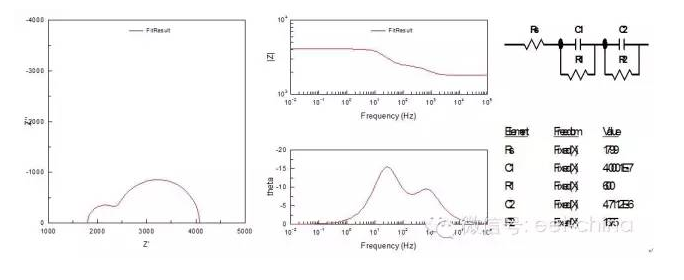
圖13.具有兩個時間常數的阻抗圖
3.8、低頻出現感抗弧的電化學體系
前面說過,當法拉第電流不僅與電極電位有關,而且受電極表面狀態變量X影響,而這個狀態變量本

弧。
當電極反應出現中間產物時,這種中間產物吸附與金屬電極表面產生表面吸附絡合物,該表面絡合物產生于電極反應的第一步,而消耗于第二步反應,而一般情況下,吸附過程的弛豫時間常數要比電雙層電容Cdl與Rt組成的充放電過程的弛豫時間常數RtCdl大的多,因此在阻抗圖的低頻部分會出現感抗弧。如圖14所示。
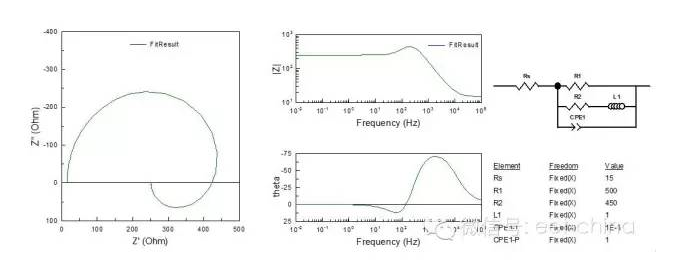
圖14.低頻出現感抗弧的阻抗圖

電容,整個EIS出現兩個容抗弧,如圖13所示。
混合電位下的阻抗譜特征
上面所述的阻抗譜均是在自然電位下測量的,而電極反應在自然電位下同時具有陰陽極兩個反應,所以阻抗譜所反映的是兩個電極反應的頻譜特征,即文獻所述的混合電位下的阻抗譜,當沒有狀態變量時,EIS仍只有一個時間常數,當有一個狀態變量影響電極反應速度時,阻抗譜會出現兩個時間常數。不過在某些情況下,需要研究單一陽極反應特征,就必須將研究電極的電位極化(弱極化區)到不同的陽極電位下進行阻抗測量,以抑制陰極反應,這就是所謂的直流偏壓下的阻抗測試,這一點在研究鈍化膜的臨界破裂電位下的阻抗特征尤為重要,它能提供點蝕誘發期的重要特征,另外在研究緩蝕劑的陽極脫附行為時也十分重要。
交流阻抗的不足之處
前面指出,對于同一組抗譜,可以找到不止一個電路能滿足它的解析,而對于同一個電路,當電路中的元件參數不同時,可以得到完全不同類型的阻抗譜,因此依靠等效電路來推測電極過程的動力學機構是一個不可靠的方法。
 電子發燒友App
電子發燒友App









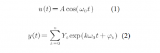


















評論