時間約束的實體解析中記錄對排序研究

摘 要:實體解析是數據集成和數據清洗的重要組成部分,也是大數據分析與挖掘的必要預處理步驟.傳統的批處理式實體解析的整體運行時間較長,無法滿足當前(近似)實時的數據應用需求.因此,研究時間約束的實體解析,其核心問題是基于匹配可能性的記錄對排序.通過對多路分塊得到的塊內信息與塊間信息分別進行分析,提出兩個基本的記錄匹配可能性計算方法.在此基礎上,提出一種基于二分圖上相似性傳播的記錄匹配可能性計算方法.將記錄對、塊及其關聯關系構建二分圖;相似性沿著二分圖不斷地在記錄對結點與塊結點之間傳播,直到收斂.收斂結果可以通過不動點計算得到.提出近似的收斂計算方法來降低計算代價,從而保證實體解析的實時召回率.最后,在兩個數據集上進行實驗評價,驗證了所提出方法的有效性,并測試方法的各個方面。

實體解析(entity resolution,簡稱ER)是數據集成和數據清洗的重要組成部分,它將數據源中描述相同實體的記錄分到同一組[1?15].大數據具有多樣性的特點,描述同一實體的記錄可能以多種形式出現,成為大數據可用性的一個瓶頸,因此,ER 是大數據分析與挖掘的必要預處理操作[15].傳統的ER 包括分塊、相似性計算和匹配決定等步驟,將整個臟數據集作為輸入,批處理之后整體輸出解析結果[1,3].在大數據時代,一方面,數據產生的速度和更新的頻率比以往更快;另一方面,大量(近似)實時的數據分析應用出現要求有限的時間內解析出盡量多的匹配記錄,稱為時間約束的實體解析(entity resolution with time constraint,簡稱TC-ER),傳統的批處理ER 無法滿足這種新需求.

當前有很多時間約束的ER 應用,例如犯罪偵查應用中要求近似實時的實體解析,希望在較短時間內解析出一部分嫌疑人記錄來,以便及時地布署偵查行動.盡管短時間內解析的結果不完整,但及時的解析結果可以大大增加抓捕到嫌疑人的可能性.再例如網購比價服務(如一淘網)中,互聯網用戶搜索了一件商品后,系統將盡快返回一部分匹配的商品條目,并逐漸優化搜索結果,這樣可以提升用戶體驗,因為眾所周知,互聯網用戶是沒有耐心的.

時間約束的ER 希望在給定的短時間(遠少于批處理運行時間)內將解析結果最大化.TC-ER 的關鍵在于實體解析過程中的記錄對選擇,即優先選擇匹配可能性大的記錄對進行解析.Whang 等人提出了3 個基于“線索”的啟發式Pay-as-you-go ER 方法,其中的“線索”分別是排序的記錄對列表、記錄集合的層次劃分和排序的記錄列表[6].Papenbrock 等人提出一組基于排序的記錄列表的漸進式ER 方法,其中,漸進式滑動窗口方法將變化的窗口多次滑過排序列表生成候選對;漸進式分塊方法將排序列表劃分成等規模小塊,然后漸進地擴大分塊范圍[7].Papenbrock 等人提出的基于排序列表的方法要優于Whang 等人提出的基于“線索”的方法[7].這些方法都假定已知最優分塊鍵或排序鍵,并且無法對記錄對進行全局排序,因此可用性和實時召回率都比較受限.由此可見,已有的時間約束的ER 方法有較大的改進空間.

本文研究時間約束的實體解析中記錄對排序,通過優先選擇匹配可能性高的記錄對進行解析,來保證實時的召回率.分塊是ER 中降低計算代價的基本的、有效的手段[16?26],然而單憑分塊方法無法實現時間約束的ER.整體而言,將分析和挖掘分塊信息來估計記錄對的相似性.將臟數據集進行多路分塊后生成有交疊的塊集合,如果一個塊包含的記錄越多,那么塊內記錄的匹配可能性越小;如果兩條記錄共同出現的塊數目越多,那么它們的匹配可能性越大.首先,基于這些直觀的思想,提出兩個基本的記錄對相似性估計方法,分別利用了塊內信息和塊間信息.接下來,通過考慮記錄對的相似性與塊的質量之間的相互影響來改進基本的相似性估計方法.將記錄對、塊及其關聯關系映射成二分圖;然后相似性在二分圖上迭代地傳播,直到收斂,獲得最終的相似性.基于圖傳播的相似性估計充分挖掘了分塊的隱藏信息,從而更有效.提出了基于不動點迭代的收斂結果計算方法,然而其計算代價較大;進一步提出了近似的收斂結果計算方法,力求在不影響記錄對相似性估計有效性的前提下降低計算代價,從而保證時間約束的ER 的實時召回率.通過實驗評估,證明了提出方法的有效性.

本文的主要貢獻總結如下:

·提出兩種基本的記錄對相似性估計方法,分別利用了塊的質量(塊內信息)和記錄與不同塊的隸屬關系(塊間信息);

·提出了基于相似性傳播的記錄對相似性估計方法,利用二分圖上可收斂的相似性傳播來衡量記錄對的相似性,通過不動點迭代來計算收斂結果,并提出了近似方法來降低計算代價;

·在兩個數據集上,通過與已有方法的對比測試,證明了本文提出方法的有效性;此外,對比了不同的相似性估計方法的表現,并測試了迭代次數對基于相似性傳播的記錄對相似性估計方法的影響.

本文第1 節定義研究的問題,并概括地介紹研究框架.第2 節介紹兩種基本的記錄對相似性估計方法.第3節提出基于二分圖上相似性傳播的記錄對相似性估計方法,并通過近似方法降低計算代價.第4 節在兩個數據集上評價本文提出的方法,驗證其有效性.第5 節介紹相關工作.最后總結全文,并指出下一步可能的研究方向.

1 研究概述

定義1(實體解析).給定一個臟數據集R={r},ER 將描述相同實體的記錄分到一組,C={ck|?ri∈ck,ri∈R∧φ(ri)=ek∧?rj∈cl∧φ(rj)=ek},其中,φ(?)是從記錄到實體的映射函數,ek 表示分組ck 對應的實體,cl 為不同于ck 的一個分組.

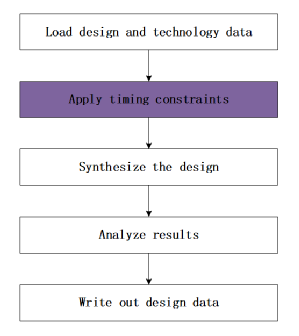
如圖1 所示,ER 傳統上是批處理操作,通常包括3 個步驟:分塊、相似度計算和匹配決定,其中,前者是可選步驟,后兩者是必要步驟[1].

Fig.1 Entity resolution model

圖1 實體解析模型

(1)相似性計算

利用記錄相似性函數計算兩條記錄的相似性,通常,相似性表示為[0,1]范圍內的數值.兩條記錄的相似性越大,匹配可能性越大,0 表示不可能匹配,1 表示完全匹配.記錄通常包括多個屬性,比如,一條個人信息的記錄包括姓名、年齡、工作單位、城市、省份和郵編等,不同的屬性需要使用不同的相似性函數來計算相似性.記錄屬性以文本型為主,以數字型為輔.針對文本屬性,目前已有多種字符串相似性函數,如TF-IDF、Q-gram、Jaccard、編輯距離等[27].針對數字屬性,則需要采用專門的函數進行比較,比如差值、漢明距離等.記錄相似性函數選擇多個屬性,分別選擇適合的相似性函數來計算屬性相似性,最后將多個屬性相似性聚集得到記錄相似性,聚集方式包括線性組合、非線性組合等,與匹配決定的策略相關.

(2)匹配決定

根據記錄的相似性來決定記錄是否匹配有兩類方法:分類和聚類.基于分類的匹配決定使用支持向量機(support vector machine,簡稱SVM)、遺傳算法、主動學習和決策樹等方法來決定記錄對是否匹配[3].一部分分類方法是監督的,需要專家標注大量的訓練數據,從而學習出有效的匹配規則(即分類器).還有一部分分類方法的匹配規則是由領域專家定義的,需要較多的領域知識.基于聚類的匹配決定使用MinCut,Markov Clustering 等聚類算法來處理成對的相似性,得到的聚類結果即為實體解析結果.同一類簇表示同一實體,不同類簇表示不同實體[2,28].本文將ER 當作分類問題,認為匹配規則已獲得,記作m(*,*),也稱為解析函數.如果m(ri,rj)返回真,記錄ri,rj 匹配;否則,m(ri,rj)返回假,記錄ri,rj 不匹配.

(3)分塊

實體解析是兩兩比較的運算,因此計算代價為平方級.當待處理的臟數據集規模較大時,計算代價將是巨大的,并且包含大量的無用計算.分塊是ER 中最常用的減小計算代價的技術[16?26],可以在不影響解析質量的前提下,有效地縮小搜索空間.分塊技術將描述可能匹配的記錄分到同一塊內,將不可能匹配的記錄分在不同的塊內.分塊通過分塊鍵(blocking key,簡稱BK)來實現,而BK 通過記錄屬性來構建.當利用一個分塊鍵對數據集進行劃分后,擁有相同分塊鍵值(blocking key value,簡稱BKV)的記錄將進入同一塊內.同一塊內的任意兩條記錄稱為候選匹配記錄對或候選對.

定義2(時間約束的實體解析).給定一個臟數據集R,傳統的ER 處理R 的時間為TER,給定時間t<

TC-ER 的流程見算法1.

算法1.TC-ER 框架.

觀察算法1 可知,TC-ER 的核心問題在于優化實體解析的順序,優先解析匹配可能性大的記錄對.如圖1 所示,在分塊與相似度計算之間增加記錄對排序.記錄對排序的依據是記錄對的匹配可能性,即估計的記錄對相似性,因此,TC-ER 的關鍵在于如何通過較小的代價準確地估計記錄對的相似性.

本文將通過分析和挖掘分塊信息來估計記錄對的相似性:(1)第2 節提出兩個基本的記錄對相似性估計方法,這兩個方法分別從分塊質量和記錄-塊的隸屬關系的角度來分析塊信息,從而估計記錄對相似性;(2)第3 節提出基于相似性傳播的記錄對相似性估計方法,將記錄對、塊及其關聯關系表示為二分圖,并通過迭代的傳播算法來挖掘分塊信息,從而改進基本的相似性估計.

定義3(多路分塊).給定一個臟數據集R={r}和一組分塊鍵的集合BK={bki|0≤i

b 表示塊,塊中的一對記錄ri,rj∈b 稱為候選對,記作〈ri,rj〉;|b|表示塊b 的規模,||b||表示塊b 的勢(cardinality),即塊內候選對的數目,記作||b||=|b|(|b|?1)/2.|B|表示塊集合B 的規模,||B||表示塊集合B 的勢,即集合內候選對的總數目.Bi 表示記錄ri 所在塊的集合.

2 基本的記錄對相似性估計

本節提出兩種基本的相似性估計方法(basic estimated similarity,簡稱BES),BES 通過直觀地分析分塊信息來計算記錄對的相似性.

2.1 基于塊質量的記錄對相似性估計

給定一個塊,這個塊包含的記錄對越多,那么這個塊內的任意一個記錄對的匹配可能性越小.將一個塊內記錄對的匹配可能性的平均值稱為塊的冗余性.一個塊的信息量是確定的,塊內的記錄對越多,那么每個記錄對平均分得的信息量就越小,塊的冗余性就越小.將用冗余性(redudancy,簡稱rd)評估塊的質量,表示為公式(1):

例如,塊b1包括一個記錄對,塊b2包括3 個記錄對,那么rd(b1)=1>rd(b2)=1/3.

給定一個記錄對〈ri,rj〉,將它所在塊的冗余性進行聚集來估計相似性,如公式(2),記作RD-ES,其中,K 是多路分塊的路數,通過K來規約,保證相似性落在[0,1]范圍:

2.2 基于Jaccard系數的記錄對相似性估計

對于一對記錄〈ri,rj〉,如果兩者共同出現在越多的塊中,那么兩者的相似性應該越大;另一方面,如果兩者分別出現在越多的不同塊中,那么兩者的差異性應該越大.通過Jaccard 系數可以表達上述思想,用一個對記錄的共同出現的塊的數目除以這對記錄各自出現的塊的并集的規模,如公式(3),記作JC-ES:

3 基于相似性傳播的記錄對相似性估計

BES 通過靜態地分析分塊信息來估計記錄對的相似性,沒有考慮記錄對相似性與塊質量的潛在的相互影響.將通過記錄對-塊之間的相似性傳播來改進BES,稱為基于相似性傳播的相似性估計(similarity propagation based estimated similarity,簡稱SP-ES).顯然,SP-ES 是以RD-ES 或者JC-ES 為基礎的.

例1:一個臟數據集d={r1,r2,r3,r4,r5,r6,r7},經過分塊得到塊集合B={b1,b2,b3,b4},b1={r1,r2,r3},b2={r2,r3},b3={r4,r5,r6},b4={r5,r7},如圖2(a)所示;塊集合可表示為記錄對形式,B′={bp1,bp2,bp3,bp4},bp1={p12,p13,p23},bp2={p23},bp3={p45,p46,p56},bp4={p57},如圖2(b)所示.關注兩個候選對p12和p45,利用兩個BES 方法估計相似性,得到如下結果:(1)RD-ES,esRD(p12)=1/3,esRD(p45)=1/3,即esRD(p12)=esRD(p45);(2)JC-ES,esJC(p12)=1/2,esJC(p45)=1/2,即esJC(p12)=esJC(p45).兩個BES 方法都認為p12和p45的相似性是相等的.然而進一步分析分塊情況發現:p23來自塊b2的相似性可以增強塊b1的冗余性,進而p12從塊b1獲得更大的相似性;而塊b3不存在此類狀況.由此可見,應該有es(p12)>es(p45).接下來,將通過相似性傳播來改進BES,解決上述問題.

Fig.2 An example of basic similarity estimations’ disadvantage

圖2 基本的記錄對相似性估計缺陷示例

3.1 相似性傳播的基本思想

本文中,相似性傳播的基本思想為:記錄對的相似性可以促進所在塊的冗余性,塊的冗余性可以促進塊內記錄對的相似性.為了充分地表示記錄對與塊之間的關聯關系,將分塊結果表示為“記錄對-塊”二分圖(嚴格描述見定義4).相似性傳播是一種基于圖結構的相似性計算方法[29,30],充分地挖隱藏信息,可以彌補其他相似性的不足.將通過例2 來直觀地了解記錄對與塊之間的相似性傳播.

定義4(“記錄對-塊”二分圖,簡稱“對-塊圖”).給定一個記錄對形式的塊集合B,B 對應的候選對集合為P,構建一個無向的二分圖G=(Vp,Vb,E),其中,Vp={vpi|0≤i≤m}為記錄對結點集合,每個記錄對結點對應一個記錄對;Vb={vbj|0≤j≤n}為塊結點集合,每個塊結點對應一個塊;E?Vp×Vb 是邊集合,表示記錄對與塊的隸屬關系.可以結合上方向來解讀邊的含義,給定一條邊,從塊結點到記錄對結點,表示“包含”關系;而從記錄對結點到塊結點,則表示“出現在”關系.本文為了便于表達,將用P 同時表示記錄對結點集合和記錄對集合,用p 同時表示記錄對結點和記錄對,用B 同時表示塊結點集合和塊集合,用b 同時表示塊結點和塊.

例2:續例1.將例1 中B′表示為二分圖G,如圖3 所示.初始時,用RD-ES 來估計記錄對相似性(es),所有塊冗余性(rd)初始化為0,得到表1 中第1 行的初始值.接下來,相似性通過二分圖傳播.

(1)P→B 傳播.以圖3(a)為例,記錄對結點p12和p13分別傳遞各自當前的相似性(都是1/3)給鄰接的塊結點bp1,p23將當前的相似性4/3 分別傳遞給鄰接的塊結點bp1和bp2;bp1獲得3 個相似性(分別為1/3,1/3,4/3),取均值為2/3 作為更新的冗余性,同理,bp2更新的冗余性為4/3,對G 所有的連通分量進行相同的操作后,得到表1 中第2 行的結果;

(2)B→P 傳播.以圖3(a)為例,塊結點bp1將當前的冗余性2/3 傳給鄰接的記錄對結點p12,p13和p23,bp2將當前的冗余性4/3 傳給鄰接的結點p23;記錄對結點p12和p13分別獲得一個冗余性2/3,分別作為各自最新的相似性,同理,p23獲得兩個冗余性2/3 和4/3,求和得到2 作為p23最新的相似性(此處為簡單的計算方式,后續將給出嚴格的計算方式),對G 所有的連通分量進行相同的操作后,得到表1 中第3 行的結果.

經過一次P→B→P 傳播后,es(p12)=2/3,es(p45)=1/3,那么es(p12)>es(p45),符合例1 中提出的預期.可見,相似性傳播有助于準確地估計記錄對的相似性,彌補基本的相似性估計方法的不足.

Fig.3 An example of pair-block barpitite graph

圖3“記錄對-塊”二分圖示例

Table 1 Example of similairity propagation on bipartite graphs

表1 二分圖上相似性傳播示例

3.2 基于對-塊圖的相似性傳播

接下來,嚴格地定義對-塊圖上相似性傳播.首先定義兩個單步傳播:從記錄對結點到塊結點(P→B)的傳播和從塊結點到記錄對結點(B→P)的傳播.然后,在單步傳播的基礎上定義迭代的相似性傳播.

定義5(P→B 傳播).給定一個對-塊圖G=(P,B,E),pij∈P,bk∈B,pij 與bk 是鄰接結點,pij 將當前的相似性傳遞給每一個鄰接的塊結點,bk 從每個鄰接記錄對結點接受相似性,并求平均值作為最新的冗余性,如公式(4)所示:

其中,N(bk)表示bk 的相鄰結點的集合.

一次P→B 傳播后,所有塊結點的冗余性將更新,而記錄對結點的相似性不變.

定義6(B→P 傳播).給定一個對-塊圖G=(P,B,E),pij∈P,bk∈B,pij 與bk 是鄰接結點,bk 將當前的冗余性傳遞給每一個鄰接的記錄對結點,pij 從每個鄰接塊結點接受冗余性,求和后除以K 作為最新的冗余性,如公式(5)所示:

一次B→P 傳播后,所有記錄對結點的相似性將更新,而塊結點的冗余性不變.

參數K 是多路分塊的路數,公式(5)中除以K 是為了將es 值規約到[0,1]范圍內,一個記錄對最多可能出現在K 個塊內.es 的規約對于后續迭代計算的收斂性非常重要.

定義7(P?B 傳播).給定一個對-塊圖G=(P,B,E),初始的記錄對相似性通過BES 得到,初始的塊冗余性為0.經過一次P→B 傳播,更新塊冗余性;再經過一次B→P 傳播,更新記錄對相似性.如此不斷迭代,直到記錄對相似性不再發生變化.容易知道,P?B 傳播是不可約、非周期、有限狀態的馬爾可夫鏈,因此必定收斂于平穩分布[29].

例3:對圖3(a)進行一次P→B→P 傳播,其中多路分塊的路數K≥2.初始時,各記錄對相似性記作es0(p12),es0(p13)和es0(p23).

(1)P→B 傳播.根據定義5,計算得到更新的塊冗余性:

(2)B→P 傳播.根據定義6,利用公式(6)的計算結果,計算得到更新的記錄對相似性:

可以發現,等式組(7)是記錄相似性的遞推關系,它隱藏了塊結點,將P→B→P 傳播轉化為P→P 傳播.

3.3 不動點計算

P?B 傳播的收斂結果計算可以作為一個不動點計算(fixpoint computation)的問題.本文主要關注記錄對相似性,因此直接使用記錄對相似性的遞推關系.將等式組(7)改寫成向量與矩陣的運算形式,如公式(8):

其中,向量為行向量.公式(8)中的3×3 矩陣是一個馬爾可夫鏈的轉移矩陣,記作Q0={qij|0≤i,j<3},qij 表示從狀態i轉移到狀態j 的概率,Q0不要求為對稱陣.特別地,K 的存在確保0≤qij≤1,并進一步保證P?B 傳播的收斂性(例3 中K≥2);如果去掉K,則Q0不再是轉移矩陣,P?B 傳播不一定收斂.計算P?B 傳播的關鍵是轉移矩陣,接下來討論如何計算轉移矩陣.

定義8(鄰接矩陣).給定一個對-塊圖G=(P,B,E),P={pi|0≤i

定義9(轉移矩陣).給定一個對-塊圖G 和對→塊鄰接矩陣Amn,那么對→塊轉移矩陣Qmn 為

同理,可以根據塊→對鄰接矩陣Anm 計算得到塊→對轉移矩陣Qnm.

用矩陣來表示P→B→P 傳播,當前記錄對的相似性向量為esx,塊的冗余性向量為rdx.那么:

(1)P→B 傳播.塊冗余性更新:

(2)B→P 傳播.記錄對相似性更新:

根據公式(12)易知,P→B→P 傳播的整體轉移矩陣為Qmm:

對于記錄對相似性,P→P 傳播與P→B→P 傳播等價,進而P?P 傳播與P?B 傳播等價.

定義10(P?P 傳播).給定一個對-塊圖G 和P→P 轉移矩陣Qmm,與P?B 傳播等價的P?P 傳播中,一次P→P 傳播可表示為

不動點計算的流程.

(1)利用BES 初始化記錄對相似性向量為es0;

(2)利用公式(14)計算下一輪記錄對相似性向量esx+1;

(3)不斷迭代步驟(2),直到殘差向量Δ(esx+1,esx)的每一維都小于ε.ε為殘差閾值,一般取一個較小常數,例如0.005;

(4)當迭代結束后,將最終的記錄對相似性向量記作essp,作為基于相似性傳播的相似性估計的結果輸出.

代價分析:P?P 傳播的一次迭代代價為O(m2),迭代次數為X,那么總代價為O(Xm2).對-塊圖G 實際是由多個連通分量組成,分量集合記作C={ci},|ci|<

3.4 近似的相似性傳播

P?P 傳播的不動點計算的代價較大,對于時間約束的ER 來說不可接受.為此,希望通過近似方法降低計算代價.下面將通過分析迭代過程中相似性傳播的情況,來說明較少的迭代次數可以近似地計算出相似性,并極大地減小計算代價.

例4:圖4 呈現了一個較大的對-塊圖,觀察記錄對p3,其初始相似性為es0(p3),第1 次P→P 傳播后,p3的相似性傳遞到p3所在塊的其他記錄對p1,p2和p4,p5,分別得到es0(p3)/6;第2 次P→P 傳播后,p3的相似性傳遞到塊b3中的記錄對p6,p7,分別得到es0(p3)/36;第3 次P→P 傳播后,p3的相似性傳遞到塊b4中的記錄對p8,p9,分別得到es0(p3)/216.可以發現:隨著迭代次數的增加,相似性傳遞得越來越遠,并且傳遞量發生指數級的衰減,而計算代價成倍增長.從物理意義的角度分析,p3與同一塊內的記錄對關聯最強,而與間接關聯的記錄對的關聯強度則隨距離增加而極大地減弱.由此得到啟發,用較少的P?P 傳播的迭代來代替不動點計算,即迭代次數X 取較小數值,如1 或2.這樣可以近似地計算出記錄對相似性,只損失微小的準確性,但可以降低計算代價,從而保證時間約束的ER 的實時召回率.將通過實驗驗證這種近似方法的有效性.

Fig.4 P?P propagation analysis

圖4 P?P 傳播分析

4 實驗評價

4.1 實驗設置

實驗代碼通過Java 實現,Java 版本為1.7.運行環境如下:處理器3.4GHz Intel(R)Core i7-2600,內存8GB,操作系統為微軟Windows 10 專業版(64 位).

·數據集.

實驗評價使用兩個數據集:一個真實數據集和一個合成數據集.真實的引文數據集DBLP-Scholar(記作DBLP)包含66 879 條引文記錄,其中有5 347 對匹配記錄,通過標題、作者、期刊/會議、年份等4 個屬性描述[3].利用Febrl 數據生成器構建一個合成的個人信息數據集(記作FB),包含150K 條個人記錄,其中有81 694 對匹配記錄,通過姓名、性別、生日、住址、城市、州和郵編等8 個屬性描述[32,33].

·評價指標.

本文的研究目標是優化實體解析順序,認為解析函數已提前確定,準確率與研究目標是正交關系,因此采用實時召回率來評估方法.在第4.3 節的部分對比測試中,還采用Top-N 命中率來評價,將在后續詳細介紹.

·解析函數.

本文采用SVM 來訓練分類器作為解析函數m(*,*)[33].

·方法設置.

對DBLP-Scholar 數據集進行四路分塊,4 個分塊鍵為標題的前3 個實詞、姓+名的前兩個字母、期刊/會議的前3 個實詞和年份.對FB 數據集進行四路分塊,4 個分塊鍵為姓+名的前兩個字母、生日、城市和郵編.漸進式滑動窗口(progressive sorted neighborhood method,簡稱PSNM)方法、漸進式分塊(progressive blocking,簡稱PB)方法和以記錄對排序列表(sorted list of record pairs,簡稱SLORP)為線索的方法的排序鍵[6,7]:DBLP-Scholar數據集上采用標題的前3 個實詞+前兩個作者的姓;FB 數據集上采用姓+名+城市.如果沒有特別說明,SP-ES 的迭代次數設置為1.TC-ER 默認采用基于RD-ES 的SP-ES 來估計記錄對相似性,記作TC-ER0;將采用基于JC-ES的SP-ES 的TC-ER 記作TC-ER1;將采用RD-ES 的TC-ER 記作TC-ER2;將采用JC-ES 的TC-ER 記作TC-ER3.

4.2 綜合測試

綜合測試將TC-ER0 與一個基準方法以及3 個已有工作進行對比.Papenbrock 等人提出的基于排序列表的PSNM 和PB 已經被證明優于Whang 等人提出的基于“線索”的方法,而基于“線索”的方法中表現最好的為SLORP[6,7],因此選擇PSNM,PB 和SLORP 這3 個方法作為比較對象.基準方法采用m(*,*)直接解析分塊后生成的候選對,記作Baseline.將隨機地生成10 個候選對順序,分別執行Baseline 方法,將10 次的結果取平均值作為Baseline 的結果.PSNM 將從小到大擴展的窗口多次滑過排序的記錄列表,PB 先根據排序的記錄列表生成同等規模的小塊,然后逐漸拓展分塊范圍,這兩個方法都漸進地生成候選對,從而優先處理匹配可能性大的記錄對[7].SLORP 通過排序的記錄列表一次性生成排序的記錄對列表,并根據記錄對順序來依次進行解析[6].PSNM,PB 和SLORP 都要依賴于排序的記錄列表,其排序鍵請參考第4.1 節中的方法設置.

圖5 和圖6 分別呈現了在DBLP 數據集上和FB 數據集上5 個方法的對比情況.

Fig.5 General test on DBLP dataset

圖5 在DBLP 數據集上的綜合測試

Fig.6 General test on FB dataset

圖6 在FB 數據集上的綜合測試

總體而言,存在TC-ER0>>PSNM,PB>SLORP>Baseline.TC-ER0 的實時召回率顯著地高于其他4 個方法;PSNM,PB 和SLORP 明顯優于Baseline;PSNM,PB 明顯優于SLORP;在前期時,PSNM 總優于PB,PB 在后期可能有機會超越PSNM(如在FB 數據集上).例如:在DBLP 數據集上,TC-ER0 花費11.5s 解析出82.47%的匹配對,PSNM 花費13s 只能解析出56.69%的匹配對,PB 花費16s 只能解析出57.18%的匹配對,SLORP 花費17s 只能解析出55.41%的匹配對,Baseline 花費18s 甚至只能解析出46.19%的匹配對;在FB 數據集上,TC-ER0 花費22s解析出88.9%的匹配對,而PSNM 花費34s 解析出62.47%的匹配對,PB 花費36s 解析出51.72%的匹配對,SLORP花費35s 解析出40.41%的匹配對,Baseline 花費42s 只能解析出33.67%的匹配對.由此可見,在較少時間預算約束下,TC-ER0 可以解析出更多的匹配對.Baseline 的實時召回率隨時間線性增長,因為它隨機地解析候選對,解析順序沒有任何優化.PSNM 在迭代中由小到大調整窗口,以此來優化候選對的解析順序;PB 通過逐漸拓展分塊范圍來優化解析順序;SLORP 通過粗糙的方法來估計候選對的相似性來優化解析順序.因此,它們的實時召回率要比Baseline 高.然而,PSNM 和PB 無法將候選對按匹配可能性排序,無法直接定位到最可能匹配的候選對;SLORP 雖然對候選進行了全排序,但其相似性估計十分粗糙,同樣無法直接定位到最可能匹配的候選對,甚至不如前兩者的表現.這些原因局限了PSNM,PB 和SLORP 的實時召回率.TC-ER0 則通過基于相似性估計的候選對排序來全局地優化解析順序,從而獲得最高的實時召回率.

再者,觀察最終召回率和運行時間.

(1)PSNM,PB 和SLORP 的最終召回率要低于TC-ER0 和Baseline.前三者只有一個排序鍵,只產生一個記錄排序列表,由此生成的候選對集合對真實的匹配對覆蓋較少;而后兩個方法,通過多路分塊生成候選對集合,可以更好地覆蓋真實的匹配對.如果將PSNM 和PB 擴展到多個排序鍵AC-PSNM 和ACPB,可以提高最終召回率,但這樣要維護多個排序列表并依次滑動,會大大增加實時的計算代價和總的計算代價,明顯降低實時召回率;

(2)就總的運行時間而言,TC-ER0,PSNM,PB 和SLORP 都比Baseline 要長,因為前四者針對解析順序的預處理操作花費了一定的時間,而Baseline 沒有預處理操作.就預處理時間而言,TC-ER0 要比PSNM,PB和SLORP 稍長一些,但它們的預處理時間占總運行時間的比例都極小.

4.3 分項測試

4.3.1 相似性估計測試

相似性估計測試將比較兩個基本的相似性估計方法RD-ES,JC-ES 和基于前兩者的SP-ES 方法在TC-ER中的表現,對應該ER 方法分別為TC-ER2(RD-ES),TC-ER3(JC-ES),TC-ER0(基于RD-ES 的SP-ES)和TC-ER1(基于JC-ES 的SP-ES).相似性估計方法的好壞將決定記錄對排序的有效性,進而影響實時召回率.圖7 和圖8 分別是在DBLP 數據集上和FB 數據集上4 個方法的對比情況,Baseline 作為參考.

Fig.7 Similarity estimation test on DBLP dataset

圖7 在DBLP 數據集上的相似性估計測試

Fig.8 Similarity estimation test on FB dataset

圖8 在FB 數據集上的相似性估計測試

整體而言,就實時召回率而言,在兩個數據集上均有TC-ER0>TC-ER1,TC-ER2>TC-ER3>Baseline.在DBLP數據集上,TC-ER0 顯著地優于其他3 個方法;TC-ER1 與TC-ER2 不相上下,但都明顯優于TC-ER3.取單點進行對比,TC-ER0 花費11.5s 解析出82.47%的匹配對,TC-ER1 花費13s 解析出78.18%的匹配對,TC-ER2 花費12s解析出71.54%的匹配對,TC-ER3 花費15s 只解析出63.41%的匹配對.在FB 數據集上,TC-ER0 顯著地優于其他3 種方法;TC-ER1 微弱地優于TC-ER2,但兩者都明顯優于TC-ER3.取單點進行對比,TC-ER0 花費22s 解析出88.9%的匹配對,TC-ER1 花費26s 解析出82.14%的匹配對,TC-ER2 花費28s 解析出75.38%的匹配對,TC-ER3花費29s 只解析出65.94%的匹配對.接下來,觀察相似性傳播對相似性估計的影響.分別對比TC-ER0 和TCER2,TC-ER1 和TC-ER3 可以發現:TC-ER 中,基于相似性傳播的相似性估計方法(TC-ER0 和TC-ER1)要明顯優于基本的相似性估計方法(TC-ER2 和TC-ER3).相似性傳播挖掘了記錄與塊之間隱藏的關聯關系,從而有效地改進了兩個基本的相似性估計方法.最后,分別對比TC-ER0 和TC-ER1,TC-ER2 和TC-ER3 可以發現:在TR-ER中,基于分塊質量的相似性估計(對應TC-ER0 和TC-ER2)要明顯優于基于Jaccard 系數的相似性估計(對應TCER1 和TC-ER3),說明分塊質量可以更有效地幫助估計記錄對的相似性.

4.3.2 SP-ES 的迭代測試

本節測試TC-ER 中SP-ES 的迭代次數對相似性估計的影響,驗證近似的相似性傳播的有效性.當殘差閾值ε=0.005 時,TC-ER0 在DBLP 數據集上和FB 數據集上分別需要7 次和11 次迭代達到收斂.將從兩個角度來進行測試:(1)在兩個數據集上,測試TC-ER0 分別進行1,2,4 和7 次迭代的實時召回率的情況,從直觀上了解隨著迭代次數的增加,相似性估計和運行時間的變化情況;(2)在兩個數據集上,測試TC-ER0 隨著迭代次數的增加直到自然收斂過程中,Top-N 命中率和啟動時間的變化情況.

TC-ER0 默認進行1 次迭代,現將TC-ER0 分別進行2m4 和7 次迭代,分別記作TC-ER0-2,TC-ER0-4 和TCER0-7.圖9 和圖10 分別展示了在DBLP 數據集上和FB 數據集上這4 種方法的對比情況,Baseline 作為參考.

Fig.9 SP-ES’s iteration test on DBLP dataset

圖9 在DBLP 數據集上SP-ES 的迭代測試

Fig.10 SP-ES’s iteration test on FB dataset

圖10 在FB 數據集上SP-ES 的迭代測試

整體而言,隨著迭代次數的增加,預處理的時間代價接近成倍地增加;然而預處理之后的實時召回率卻沒有明顯的提升,即相似性估計的準確性只是非常微弱地提高.取單點來對比,在DBLP 數據集上,運行時間為7s 時,TC-ER0 的實時召回率為65.63%,而TC-ER0-2 約為40%,TC-ER0-4 和TC-ER0-7 都為0;在FB 數據集上,運行時間為18s 時,TC-ER0 的實時召回率超過70%,而TC-ER0-2 為32.47%,TC-ER0-4 和TC-ER0-7 都為0.直觀來看,基于1 次迭代SP-ES 對于TC-ER 來說是最佳的選擇.

接下來,從Top-N 命中率和啟動時間的角度來分析迭代的效果,Top-N 命中率是指在觀測的前N 次比較中匹配對占的比例,啟動時間是指TC-ER0 從啟動運行到開始產生解析結果的時間間隔.將數據集中真實的匹配對數目設為N,那么,在DBLP 數據集上N=5347,在FB 數據集上N=81694.圖11、圖12 展示了TC-ER0 方法在兩個數據集上的Top-N 命中率(對應主軸刻度)和啟動時間(對應次軸刻度)隨迭代次數增加而變化的情況.可以發現:隨著迭代次數的增加,命中率的提高非常小,而啟動時間則幾乎是線性增長.由此可知,迭代次數的增加不會明顯提高相似性估計的準確性,而啟動時間大幅增長.結合圖9、圖10 可知:隨著迭代次數的增加,實時召回率曲線的趨勢變化微弱,大體上是整體向后平移,啟動時間占總運行時間比重大幅增加.這導致解析結果輸出推遲,影響TC-ER0 的表現.綜上分析,為了兼顧時效性和召回率,應當選擇較少的迭代次數,1 次迭代是TC-ER0 的最好選擇.

Fig.11 SP-ES’s hitting rate &start-up time tests on DBLP dataset

圖11 在DBLP 數據集上SP-ES 的Top-N 命中率及啟動時間測試

Fig.12 SP-ES’s hitting rate &start-up time tests on FB dataset

圖12 在FB 數據集上SP-ES 的Top-N 命中率及啟動時間測試

5 相關工作

實體解析是數據集成與數據清洗不可或缺的組成部分,也稱為實體識別、實體匹配、記錄鏈接等[1?15].傳統的實體解析是批處理操作,將整個數據集輸入,經過分塊、相似性計算和匹配決定后,輸出解析結果[1,2].這種整體解析的運行時間通常比較長.隨著大數據產業的發展,數據產生的速度和更新的頻率與以往相比都有了質的飛躍,而一些數據應用要求(近似)實時的響應,因此時間約束的ER 成為研究熱點[6,7].與本文相關的研究還包括分塊技術和基于圖的相似性傳播.

Whang 等人提出了Pay-as-you-go 實體解析的概念:在運行時間或計算資源有限的情況下,使得實體解析的輸出結果最大化;并定義了“線索”的概念,幫助預測哪些記錄的匹配可能性更大,它需要與已有的ER 方法結合起來使用[6].Papenbrock 等人提出了一組時間約束的ER 方法,它們都基于排序的記錄列表[7].漸進式滑動窗口(progressive sorted neighborhood method,簡稱PSNM)通過從小到大擴大窗口來多次滑過列表,漸進地生成候選對;漸進式分塊(progressive blocking,簡稱PB)先根據記錄列表生成同樣規模的小塊,然后逐漸拓展分塊范圍,漸進地生成候選對.在此基礎上,還對兩個方法進行了多屬性擴展,同時生成多個排序列表,并交替地對排序列表執行PSNM 和PB,從而提高總的召回率,但同時也降低了漸進性.這兩類方法都無法將所有候選對按匹配可能性進行全局排序,限制了實時召回率;再者,兩類方法都依賴于已知的分塊鍵或排序鍵,限制了適用范圍.

分塊是ER 中最常用的降低時間開銷的技術,它可以有效地縮小搜索空間[16?26].分塊方法可分為兩類:基于分塊鍵的方法和基于排序鍵的方法.前者定義分塊鍵(blocking key,簡稱BK),然后根據每條記錄的屬性信息生成對應的分塊鍵值(blocking key value,簡稱BKV),最后將擁有相同BKV 的記錄分在同一塊內,分塊方法以此類居多[17?20,23?26].后者也稱為滑動窗口方法,首先定義排序鍵,然后將記錄按排序鍵值排序,最后將一個窗口在記錄列表上滑動來生成候選對[21,22].

基于圖的相似性傳播可以挖掘結構信息來計算數據對象(data object)之間的相似性,這類方法已經應用在了多個領域,如模式匹配[29]、聯合式實體解析[4]、推薦系統[30]等.Melnick 等人設計了SF(similarity flooding)算法來幫助模式匹配,但其應用范圍不局限于此[29].將兩個關系模式分別構建成模式圖,并根據領域知識計算出兩個圖之間結點的初步的相似性,將這兩個圖作為SF 算法的輸入.SF 將兩個圖中的結點建立映射關系,并構建成一個成對的關聯圖,圖中的每個結點對應原模式圖中一個映射結點對,例如關聯圖中的三元組((x,y),p,(x′,y′)),對應模式圖中的兩個三元組(x,p,x′)和(y,p,y′).相似性通過((x,y),p,(x′,y′))的正向和反向不斷迭代地傳播,迭代停止時每個結點上的對象對(例如(x,y))獲得最終的相似性.利用SF 最終的相似性可以決定模式匹配的結果.SF 通過不動點計算來獲得最終的相似性.如果相似性收斂,那么SF 自然終止;如果不收斂,則運行到SF 設定的最大迭代次數時終止.Simrank 是一個更通用的兩兩(pairwise)相似性計算方法,其基本思想是:如果與兩個對象關聯的對象是相似的,那么這兩個對象也是相似的[30].Simrank 將一個有向的對象圖轉換成一個有向的對象對圖,對象對圖與SF 中的成對關聯圖類似,也是((x,y),p,(x′,y′))的形式.在對象對圖中,初始時將由同一對象組成的結點的相似性設為1,其他結點的相似性為0.然后相似性在對象對圖中沿著有向邊不斷傳遞,直到收斂.在傳遞過程中,一個結點(x,y)將相似性經過衰減少后傳給它所有指向的結點;另一個結點(x′,y′)從指向它的所有結點處獲得相似性,取均值作為自己最新的相似性.Simrank 保證收斂性,可以通過不動點計算獲得收斂結果.Dong 等人通過相似性傳播來解析關聯的數據,例如引文數據、電影數據等[4].以引文數據為例,文章、作者及會議之間存在語義關聯,如果兩個文章記錄是匹配的,那么它們的作者記錄的匹配可能性將會增加.將關聯的數據構建依賴圖,其中,邊既有單向的,也有雙向的.根據文本相似性來計算每個結點的初始相似性,然后,相似性通過有向邊來傳播.當某個結點的相似性超過閾值,就認為它對應的記錄是匹配的,匹配的結點將進入非激活狀態.不斷迭代,直到所有結點都被解析完.以上3 種相似性傳播都是在對象(記錄)之間的傳播,而本文的相似性傳播則是在記錄與塊之間進行.

當前,還出現了一些新型的ER 方法:Ramadan 等人提出了面向查詢的ER 方法[5];Kushagrat 等人針對ER 中聚類問題,提出了選擇策略[8];Lin 等人提出了面向異構記錄的ER 方法[9];多個研究團隊提出了基于圖的ER 方法[10?12];多個研究團隊提出了基于深度學習的ER 方法[13,14].

6 結束語

時間約束的實體解析是大數據研究的熱點問題,本文研究時間約束的ER 中記錄對相似性估計與排序.在多路分塊的基礎上,分析塊內信息,提出了基于塊質量的記錄對相似性估計方法;分析塊間信息,提出了基于Jaccard 系數的記錄對相似性估計方法.針對兩個基本的相似性估計方法,提出了基于相似性圖傳播的改進.構建記錄對和塊組成的二分圖.在二分圖上運行相似性傳播,在此過程中記錄對的相似性動態變化,直到收斂.提出了基于不動點迭代的收斂結果計算方法,并提出了近似方法來降低計算代價.在一個真實數據集和一個合成數據集上測試提出的方法,證明其有效性,并測試了提出方法的各個方面的特點.在未來的工作中,將研究聯合式實體解析在時間約束條件下的解決方案。

審核編輯：湯梓紅