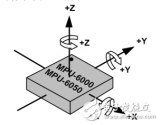
使用MPU6050硬件DMP解算姿態(tài)是非常簡單的，下面介紹由三軸陀螺儀和加速度計的值來使用四元數(shù)軟件解算姿態(tài)的方法。

　　我們先來看看如何用歐拉角描述一次平面旋轉(zhuǎn)（坐標變換）：

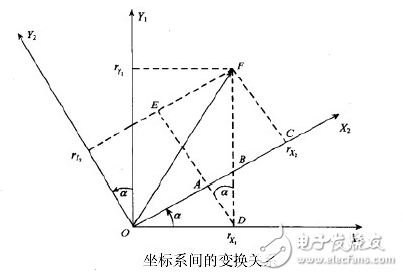
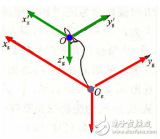
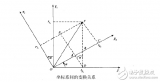
　　設(shè)坐標系繞旋轉(zhuǎn)α角后得到坐標系，在空間中有一個矢量在坐標系中的投影為，在內(nèi)的投影為由于旋轉(zhuǎn)繞進行，所以Z坐標未變，即有。

　　轉(zhuǎn)換成矩陣形式表示為：

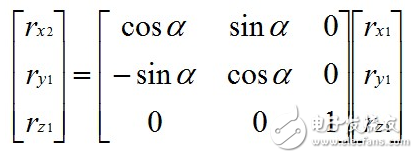
　　整理一下：

　　所以從旋轉(zhuǎn)到可以寫成上面僅僅是繞一根軸的旋轉(zhuǎn)，如果三維空間中的歐拉角旋轉(zhuǎn)要轉(zhuǎn)三次：

　　上面得到了一個表示旋轉(zhuǎn)的方向余弦矩陣。

　　不過要想用歐拉角解算姿態(tài)，其實我們套用歐拉角微分方程就行了：

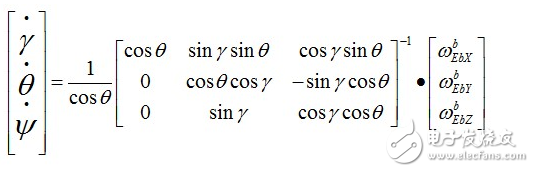
　　上式中左側(cè)，是本次更新后的歐拉角，對應(yīng)row、pit、yaw。右側(cè)，是上個周期測算出來的角度，三個角速度由直接安裝在四軸飛行器的三軸陀螺儀在這個周期轉(zhuǎn)動的角度，單位為弧度，計算間隔時T陀螺角速度，比如0.02秒0.01弧度/秒=0.0002弧度。間因此求解這個微分方程就能解算出當(dāng)前的歐拉角。

　　前面介紹了什么是歐拉角，而且歐拉角微分方程解算姿態(tài)關(guān)系簡單明了，概念直觀容易理解，那么我們?yōu)槭裁床挥脷W拉角來表示旋轉(zhuǎn)而要引入四元數(shù)呢？

　　一方面是因為歐拉角微分方程中包含了大量的三角運算，這給實時解算帶來了一定的困難。而且當(dāng)俯仰角為90度時方程式會出現(xiàn)神奇的“GimbalLock”。所以歐拉角方法只適用于水平姿態(tài)變化不大的情況，而不適用于全姿態(tài)飛行器的姿態(tài)確定。

　　四元數(shù)法只求解四個未知量的線性微分方程組，計算量小，易于操作，是比較實用的工程方法。

　　我們知道在平面（x，y）中的旋轉(zhuǎn)可以用復(fù)數(shù)來表示，同樣的三維中的旋轉(zhuǎn)可以用單位四元數(shù)來描述。我們來定義一個四元數(shù)：

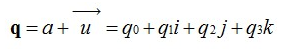
　　我們可以把它寫成，其中，。那么是矢量，表示三維空間中的旋轉(zhuǎn)軸。w是標量，表示旋轉(zhuǎn)角度。那么就是繞軸旋轉(zhuǎn)w度，所以一個四元數(shù)可以表示一個完整的旋轉(zhuǎn)。只有單位四元數(shù)才可以表示旋轉(zhuǎn)，至于為什么，因為這就是四元數(shù)表示旋轉(zhuǎn)的約束條件。

　　而剛才用歐拉角描述的方向余弦矩陣用四元數(shù)描述則為：

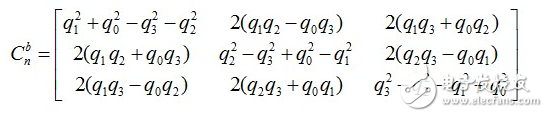
　　所以在軟件解算中，我們要首先把加速度計采集到的值（三維向量）轉(zhuǎn)化為單位向量，即向量除以模，傳入參數(shù)是陀螺儀x、y、z值和加速度計x、y、z值：

　　void IMUupdate（float gx， float gy， float gz， float ax， float ay， float az）

　　{ float norm;

　　float vx， vy， vz; float ex， ey， ez;

　　norm = sqrt（ax*ax + ay*ay + az*az）;

　　ax = ax / norm;

　　ay = ay / norm;

　　az = az / norm;

　　下面把四元數(shù)換算成方向余弦中的第三行的三個元素。剛好vx、vy、vz 。其實就是上一次的歐拉角（四元數(shù)）的機體坐標參考系換算出來的重力的單位向量。

　　estimated direction of gravity vx = 2*（q1*q3 - q0*q2）;

　　vy = 2*（q0*q1 + q2*q3）;

　　vz = q0*q0 - q1*q1 - q2*q2 + q3*q3;

　　axyz是機體坐標參照系上，加速度計測出來的重力向量，也就是實際測出來的重力向量。

　　axyz是測量得到的重力向量，vxyz是陀螺積分后的姿態(tài)來推算出的重力向量，它們都是機體坐標參照系上的重力向量。

　　那它們之間的誤差向量，就是陀螺積分后的姿態(tài)和加計測出來的姿態(tài)之間的誤差。

　　向量間的誤差，可以用向量叉積（也叫向量外積、叉乘）來表示，exyz就是兩個重力向量的叉積。

　　這個叉積向量仍舊是位于機體坐標系上的，而陀螺積分誤差也是在機體坐標系，而且叉積的大小與陀螺積分誤差成正比，正好拿來糾正陀螺。（你可以自己拿東西想象一下）由于陀螺是對機體直接積分，所以對陀螺的糾正量會直接體現(xiàn)在對機體坐標系的糾正。

　　integral error scaled integral gain exInt = exInt + ex*Ki;

　　eyInt = eyInt + ey*Ki;

　　ezInt = ezInt + ez*Ki;

　　用叉積誤差來做PI修正陀螺零偏

　　integral error scaled integral gain exInt = exInt + ex*Ki;

　　eyInt = eyInt + ey*Ki;

　　ezInt = ezInt + ez*Ki; // adjusted gyroscope measurements

　　gx = gx + Kp*ex + exInt;

　　gy = gy + Kp*ey + eyInt;

　　gz = gz + Kp*ez + ezInt;

　　四元數(shù)微分方程，其中T為測量周期，為陀螺儀角速度，以下都是已知量，這里使用了一階龍哥庫塔求解四元數(shù)微分方程：

　　integrate quaternion rate and normalise

　　q0 = q0 + （-q1*gx - q2*gy - q3*gz）*halfT;

　　q1 = q1 + （q0*gx + q2*gz - q3*gy）*halfT;

　　q2 = q2 + （q0*gy - q1*gz + q3*gx）*halfT;

　　q3 = q3 + （q0*gz + q1*gy - q2*gx）*halfT;

　　最后根據(jù)四元數(shù)方向余弦陣和歐拉角的轉(zhuǎn)換關(guān)系，把四元數(shù)轉(zhuǎn)換成歐拉角：

　　所以有：

　　ANGLE.Yaw = atan2（2 * q1 * q2 + 2 * q0 * q3， -2 * q2*q2 - 2 * q3* q3 + 1）* 57.3; // yaw

　　ANGLE.Y= asin（-2 * q1 * q3 + 2 * q0* q2）* 57.3; // pitch

　　ANGLE.X= atan2（2 * q2 * q3 + 2 * q0 * q1， -2 * q1 * q1 - 2 * q2* q2 + 1）* 57.3; // roll