卷積的定義
卷積是兩個變量在某范圍內相乘后求和的結果。
如果卷積的變量是序列x(n)和h(n),則卷積的結果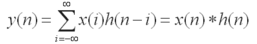 ,其中星號*表示卷積。
,其中星號*表示卷積。
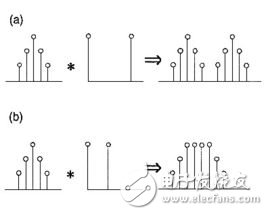
當時序n=0時,序列h(-i)是h(i)的時序i取反的結果;時序取反使得h(i)以縱軸為中心翻轉180度,所以這種相乘后求和的計算法稱為卷積和,簡稱卷積。
另外,n是使h(-i)位移的量,不同的n對應不同的卷積結果。如果卷積的變量是函數x(t)和h(t),則卷積的計算變為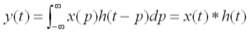 ,
,
其中p是積分變量,積分也是求和,t是使函數h(-p)位移的量,星號*表示卷積。
卷積的定理
卷積定理指出,函數卷積的傅里葉變換是函數傅里葉變換的乘積。即,一個域中的卷積相當于另一個域中的乘積,例如時域中的卷積就對應于頻域中的乘積。
F(g(x)*f(x))=F(g(x))F(f(x))
其中F表示的是傅里葉變換。
這一定理對拉普拉斯變換、雙邊拉普拉斯變換、Z變換、Mellin變換和Hartley變換(參見Mellininversiontheorem)等各種傅里葉變換的變體同樣成立。在調和分析中還可以推廣到在局部緊致的阿貝爾群上定義的傅里葉變換。
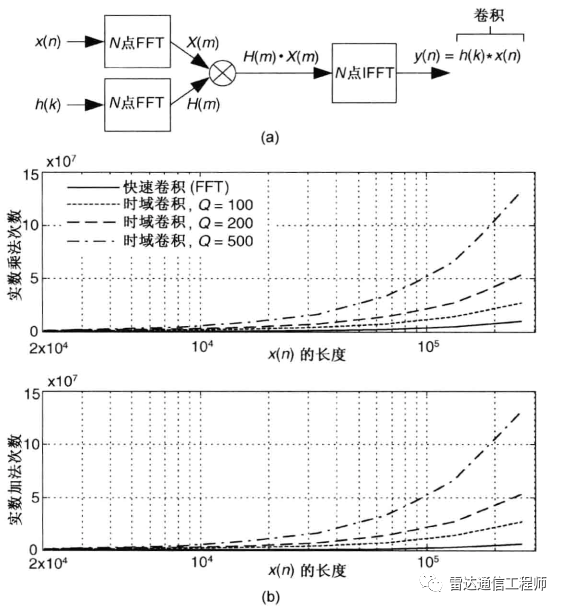
利用卷積定理可以簡化卷積的運算量。對于長度為n的序列,按照卷積的定義進行計算,需要做2n-1組對位乘法,其計算復雜度為;而利用傅里葉變換將序列變換到頻域上后,只需要一組對位乘法,利用傅里葉變換的快速算法之后,總的計算復雜度為。這一結果可以在快速乘法計算中得到應用。
卷積的意義
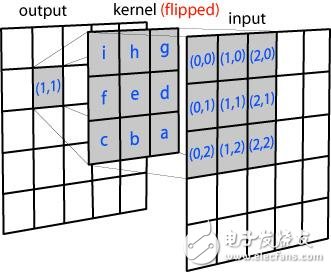
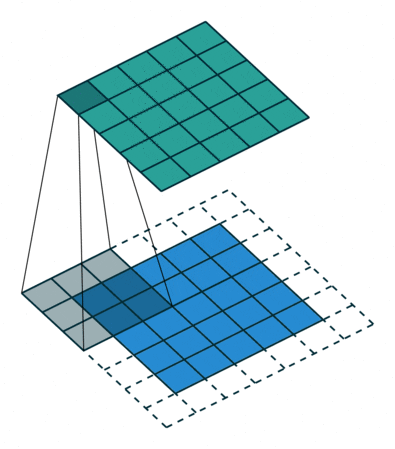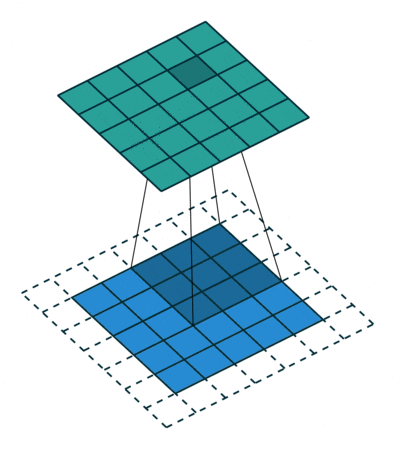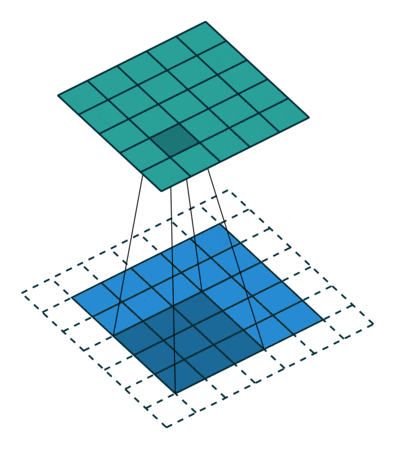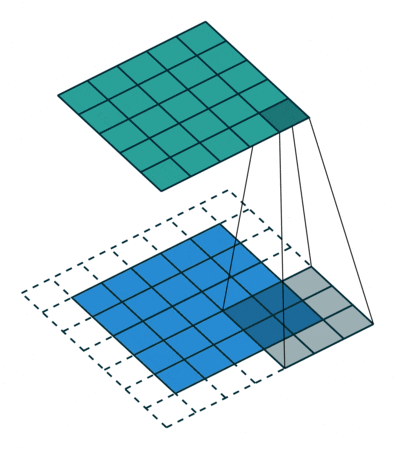
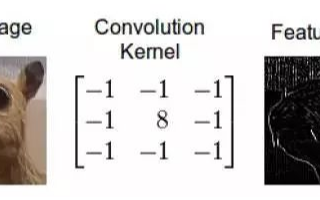
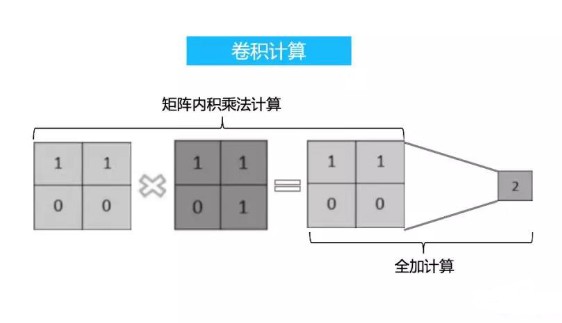
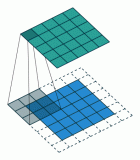
用一個模板和一幅圖像進行卷積,對于圖像上的一個點,讓模板的原點和該點重合,然后模板上的點和圖像上對應的點相乘,然后各點的積相加,就得到了該點的卷積值。對圖像上的每個點都這樣處理。由于大多數模板都是對稱的,所以模板不旋轉。卷積是一種積分運算,用來求兩個曲線重疊區域面積。可以看作加權求和,可以用來消除噪聲、特征增強。
把一個點的像素值用它周圍的點的像素值的加權平均代替。
加權疊加:對于線性時不變系統,如果知道該系統的單位響應,那么將單位響應和輸入信號求卷積,就相當于把輸入信號的各個時間點的單位響應加權疊加,就直接得到了輸出信號。
通俗的說:
在輸入信號的每個位置,疊加一個單位響應,就得到了輸出信號。
這正是單位響應是如此重要的原因。
在輸入信號的每個位置,疊加一個單位響應,就得到了輸出信號。
這正是單位響應是如此重要的原因。
在輸入信號的每個位置,疊加一個單位響應,就得到了輸出信號。
這正是單位響應是如此重要的原因。
卷積的應用
卷積是一種線性運算,圖像處理中常見的mask運算都是卷積,廣泛應用于圖像濾波。
卷積關系最重要的一種情況,就是在信號與線性系統或數字信號處理中的卷積定理。利用該定理,可以將時間域或空間域中的卷積運算等價為頻率域的相乘運算,從而利用FFT等快速算法,實現有效的計算,節省運算代價。
在工程和數學上的應用
統計學中,加權的滑動平均是一種卷積。概率論中,兩個統計獨立變量X與Y的和的概率密度函數是X與Y的概率密度函數的卷積。聲學中,回聲可以用源聲與一個反映各種反射效應的函數的卷積表示。電子工程與信號處理中,任一個線性系統的輸出都可以通過將輸入信號與系統函數(系統的沖激響應)做卷積獲得。物理學中,任何一個線性系統(符合疊加原理)都存在卷積。
介紹一個實際的概率學應用例子。假設需求到位時間的到達率為poisson(λ)分布,需求的大小的分布函數為D(。),則單位時間的需求量的分布函數為F(x):
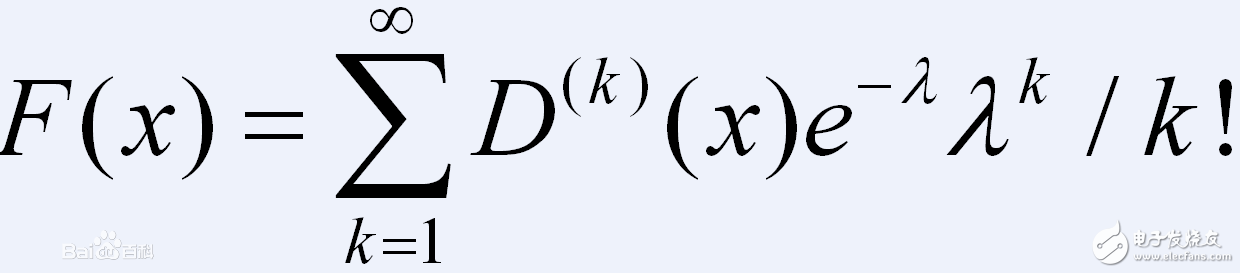
其中D(k)(x)為k階卷積。
卷積是一種線性運算,圖像處理中常見的mask運算都是卷積,廣泛應用于圖像濾波。castlman的書對卷積講得很詳細。
高斯變換就是用高斯函數對圖像進行卷積。高斯算子可以直接從離散高斯函數得到:
for(i=0;i《N;i++)
{
for(j=0;j《N;j++)
{
g[i*N+j]=exp(-((i-(N-1)/2)^2+(j-(N-1)/2)^2))/(2*delta^2));
sum+=g[i*N+j];
}
}
再除以sum得到歸一化算子
N是濾波器的大小,delta自選
首先,在提到卷積之前,必須提到卷積出現的背景。卷積是在信號與線性系統的基礎上或背景中出現的,脫離這個背景單獨談卷積是沒有任何意義的,除了那個所謂褶反公式上的數學意義和積分(或求和,離散情況下)。
信號與線性系統,討論的就是信號經過一個線性系統以后發生的變化(就是輸入輸出和所經過的所謂系統,這三者之間的數學關系)。所謂線性系統的含義,就是,這個所謂的系統,帶來的輸出信號與輸入信號的數學關系式之間是線性的運算關系。
因此,實際上,都是要根據我們需要待處理的信號形式,來設計所謂的系統傳遞函數,那么這個系統的傳遞函數和輸入信號,在數學上的形式就是所謂的卷積關系。
卷積關系最重要的一種情況,就是在信號與線性系統或數字信號處理中的卷積定理。利用該定理,可以將時間域或空間域中的卷積運算等價為頻率域的相乘運算,從而利用FFT等快速算法,實現有效的計算,節省運算代價。
在地震中的應用
地震勘探中,在地表激發點激發的地震子波(seismicwavelet)向地下傳播,當遇到地下波阻抗界面時,一部分能量就會作為反射地震波向上反射回地表,被地面的傳感器接收,隨著地震波不斷向下傳播、反射、接收,就會記錄一系列時間延遲的地震波(大地濾波后的地震子波),稱為地震記錄。這一過程或地震記錄可以用數學模型描述。如果假設地下介質為古皮奧(Goupilaud)的水平層狀介質模型,子波為雷克(Ricker)子波,地震記錄可以看作是由震源子波與地下反射率函數、多次反射、儀器等諸多因素的相褶積的過程,令x(t),w(t)和n(t)分別表示地震記錄,地震子波及噪聲,褶積過程數學模型描述為:長期以來,褶積模型廣泛用于描述地震信號。顧名思義,反褶積就是褶積的逆過程,從地震記錄x(t)中恢復出反射率函數r(t)。
 電子發燒友App
電子發燒友App








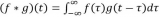

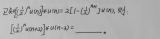











評論