卷積過程是卷積神經網絡最主要的特征。然而卷積過程有比較多的細節，初學者常會有比較多的問題，這篇文章對卷積過程進行比較詳細的解釋。

1、卷積運算

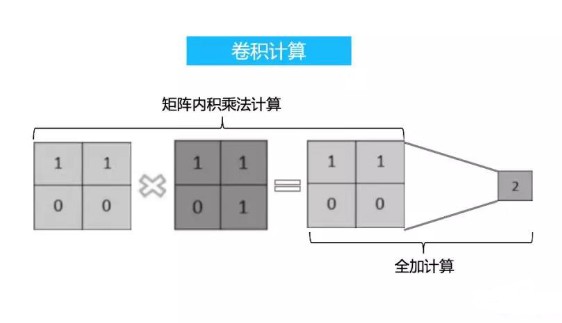
首先我們需要知道什么是卷積計算，它其實是一種簡單數學運算，有兩個步驟：一個是矩陣內積乘法，另一個是將內積乘法的結果進行全加。

（1）矩陣內積乘法

矩陣的內積乘法非常簡單，就是把兩個相乘的矩陣，相同位置的元素進行乘法運算，這個時候會得到一個新的矩陣（在這里我們需要注意一下，卷積是在作矩陣內積乘法，而不是矩陣乘法）。

（2）全加計算

這個新矩陣的全部值會進行相加，然后會得到一個值，這個值才是卷積運算的結果。

卷積計算過程如下圖所示：

2、特征圖像與卷積核

對于實際的卷積過程中，它一方面有輸入圖像，這些圖像被稱作是特征圖像（注：卷積神經網絡中，原始的輸入是真實的圖像，經過卷積后會生成特征圖像），另一方面還需要有卷積核。

卷積核的值是人為設定的，它是可以調節的，在實際的卷積神經網絡中，卷積核的值就是網絡的參數。對卷積網絡進行訓練，就是在調節這些卷積核心的參數。在實際中一般不會用太大的卷積核，常見的卷積核大小有3*3，5*5，1*1的大小。

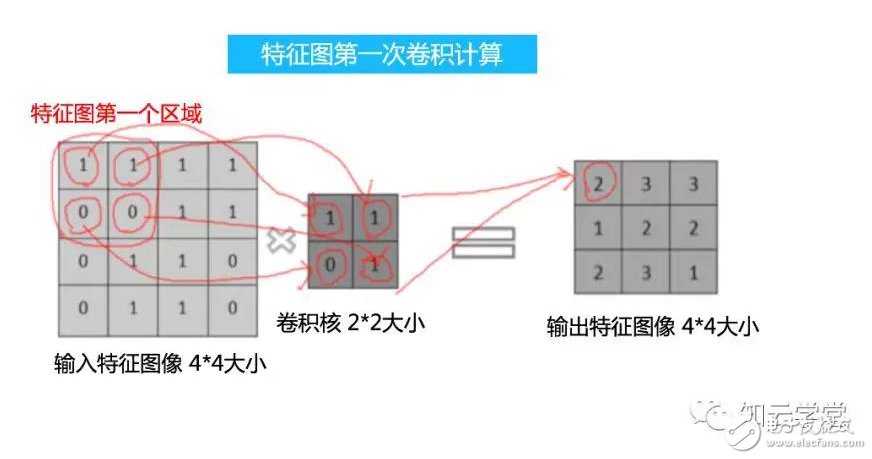
特征圖像和卷積核都是以矩陣的形式存在，因此它們可以進行卷積計算。卷積計算的輸入不僅可以是圖像，還可以是其它的二維矩陣信息（當然還有一維和三維的卷積，這里就不多介紹了）。卷積核首先會對特征圖像的第一個區域進行卷積運算，這個卷積計算的結果，會作為輸出特征圖像上的一個點，如下圖所示。

3、卷積核在特征圖像上的滑動過程

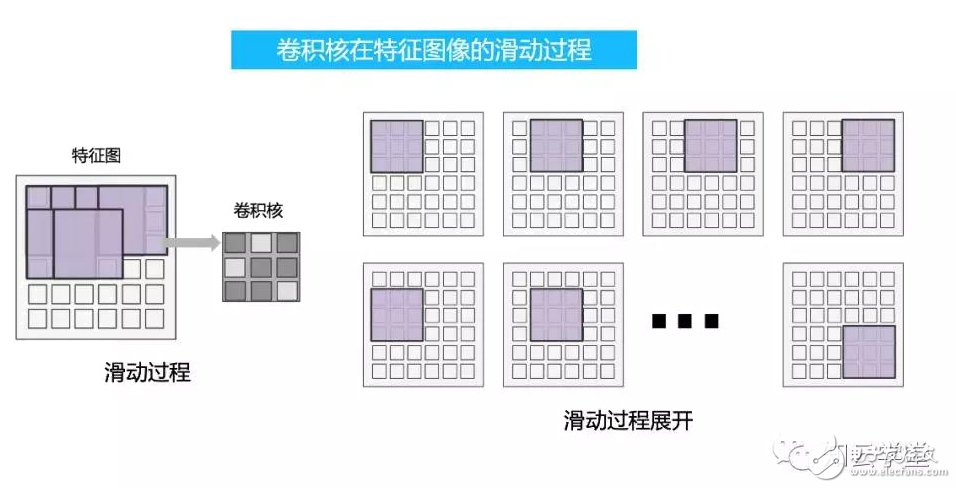
每次卷積計算的結果會作為輸出特征圖像的一個點，而特征圖像在進行卷積過程后，會輸出一幅新的特征圖像，這需要卷積核與特征圖像進行多次卷積計算。形象的來說，卷積核會在輸入的特征圖像上滑動。這個滑動的過程，一般是沿著從左到右，從上到下這樣的次序。如下圖所示。

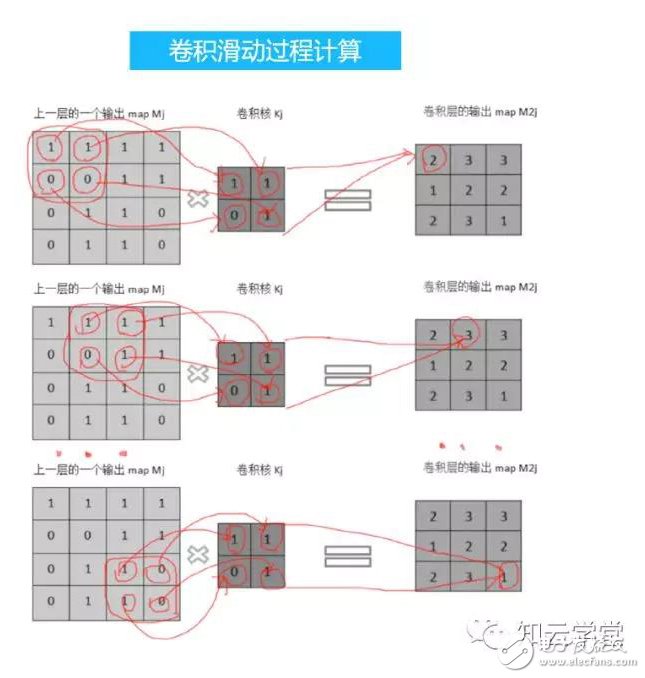
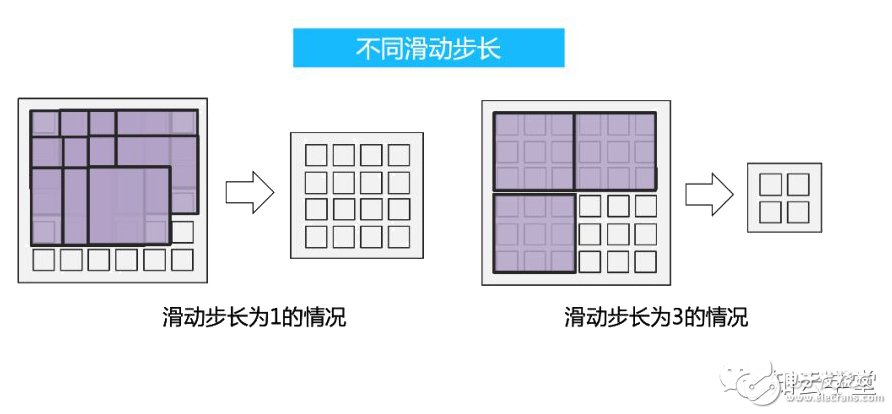
這里還需要注意的是滑動的步長，上面所說的是滑動的步長為1的情況。滑動的步長還可以取不為1的情況，不同的滑動步長，輸出特征圖的大小不同，如下圖所示。

4、多通道特征圖像的卷積過程

使用一個卷積核對一幅特征圖像進行卷積之后，會產生一幅新的特征圖像，所以我們很自然的能想到，使用多個卷積核對特征圖像進行卷積會得到多幅特征圖像。在一個實際卷積神經網絡中通常有很多個卷積層次，每個卷積層都有很多個卷積核，那么在每個層次也會產生很多幅特征圖像，這些特征圖像的數目，被稱為是“通道”數目。

此時會面臨一個問題是，怎樣對多個通道的特征像進行卷積。這個時候我們需要對卷積核進行分組，每組卷積核的數目，對應的是輸入通道特征圖像的數目，而輸出通道的數目是卷積核一共有多少組。所以總的卷積核心數目是：輸入通道數目*輸出通道數目。

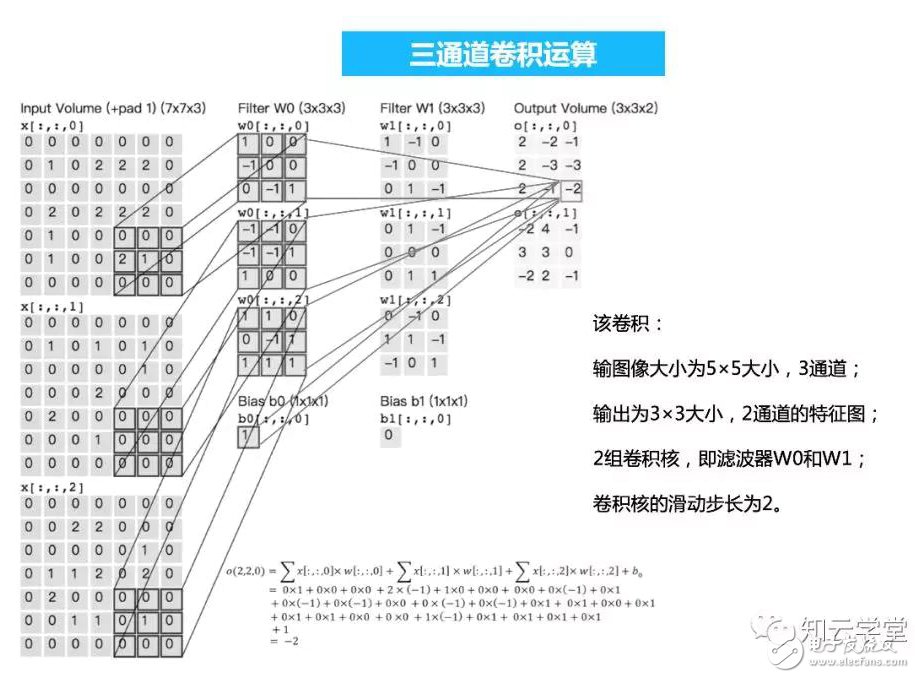
另外還需要注意的是，每組卷積核心通常還有一個偏置項，所以下圖的卷積過程是，第一組的三個卷積核進行卷積計算后的結果，再加上一個偏執項的值，才是輸出特征相應位置的值。

還需要注意的是，輸入特征圖的外圍經常會填充一圈的零，這樣的處理是為了讓特征圖邊緣的值能對準卷積核，可以減少一些信息的損失。

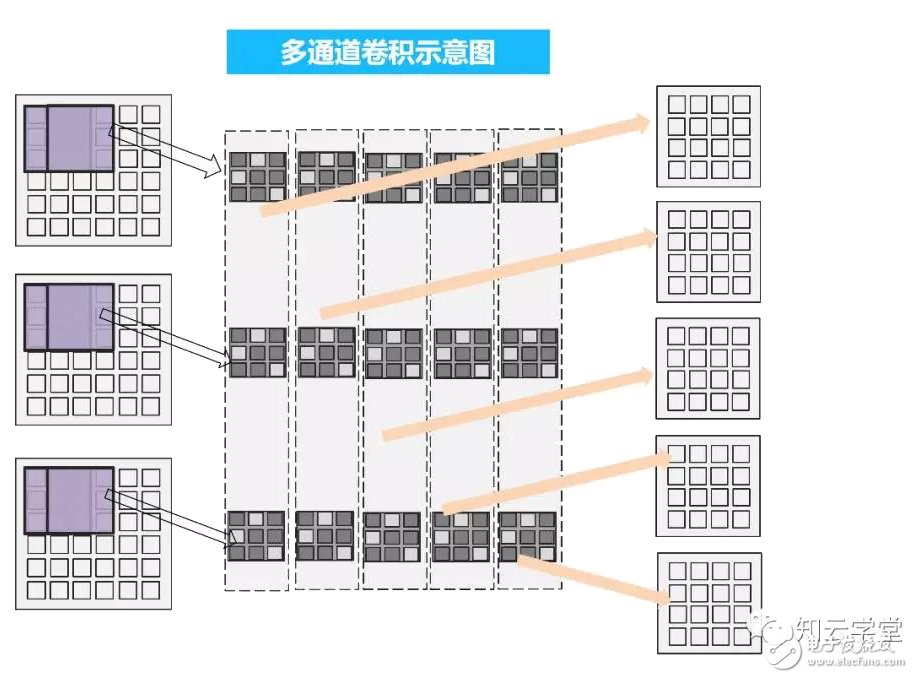
下面兩幅圖是多通道卷積過程的示意圖。

后記

理解卷積過程對于學習深度神經網絡非常重要，在這篇文章對卷積過程進行了較為詳細的解釋。其實基本的卷積過程并不復雜，但是有一些細節需要多去思考才能消化。另外現在人們對卷積神經網絡特性，也有了越來越深入的認識......