加法器的簡介
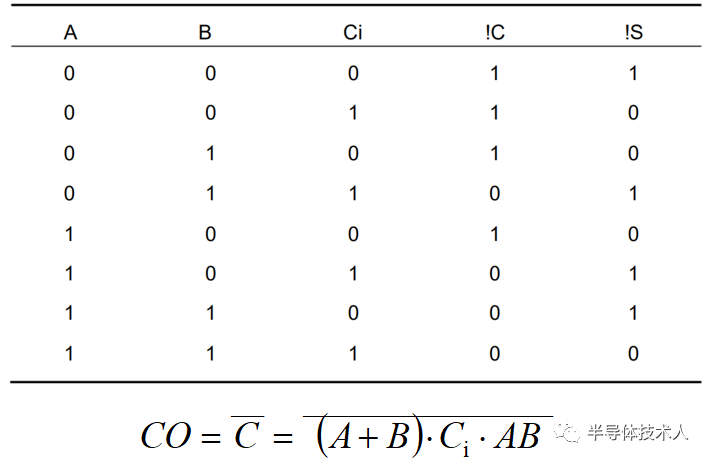
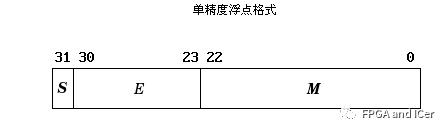
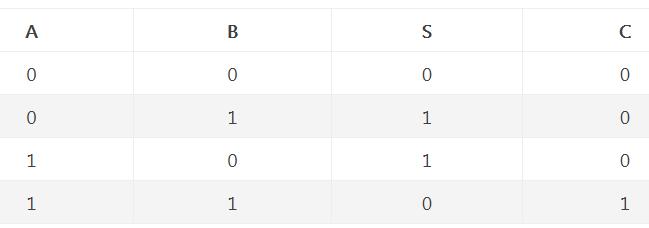
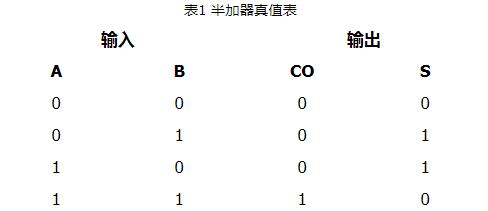
加法器是為了實現加法的。即是產生數的和的裝置。加數和被加數為輸入,和數與進位為輸出的裝置為半加器。若加數、被加數與低位的進位數為輸入,而和數與進位為輸出則為全加器。常用作計算機算術邏輯部件,執行邏輯操作、移位與指令調用。對于1位的二進制加法,相關的有五個的量:
1,被加數A,
2,被加數B,
3,前一位的進位CIN,
4,此位二數相加的和S,
5,此位二數相加產生的進位COUT。前三個量為輸入量,后兩個量為輸出量,五個量均為1位。對于32位的二進制加法,相關的也有五個量:
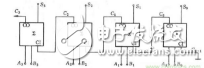
加法器的原理
1,被加數A(32位),
2,被加數B(32位),
3,前一位的進位CIN(1位),
4,此位二數相加的和S(32位),
5,此位二數相加產生的進位COUT(1位)。
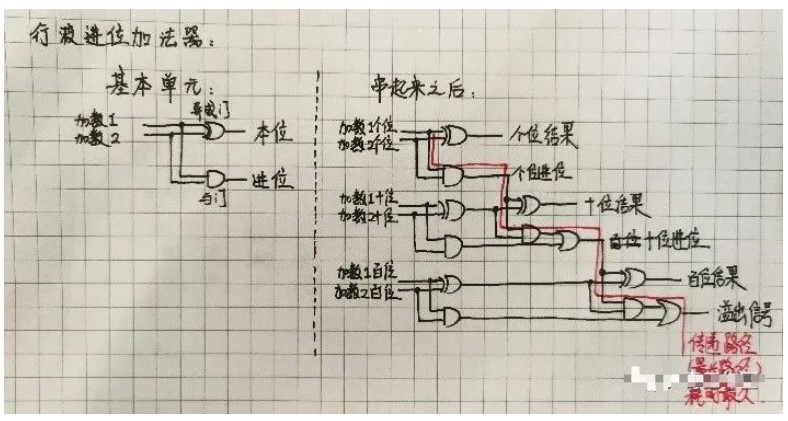
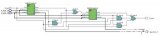
要實現32位的二進制加法,一種自然的想法就是將1位的二進制加法重復32次(即逐位進位加法器)。這樣做無疑是可行且易行的,但由于每一位的CIN都是由前一位的COUT提供的,所以第2位必須在第1位計算出結果后,才能開始計算;第3位必須在第2位計算出結果后,才能開始計算,等等。而最后的第32位必須在前31位全部計算出結果后,才能開始計算。這樣的方法,使得實現32位的二進制加法所需的時間是實現1位的二進制加法的時間的32倍。
可以看出,上法是將32位的加法1位1位串行進行的,要縮短進行的時間,就應設法使上敘進行過程并行化。逐位進位加法器,在每一位的計算時,都在等待前一位的進位。那么不妨預先考慮進位輸入的所有可能,對于二進制加法來說,就是0與1兩種可能,并提前計算出若干位針對這兩種可能性的結果。等到前一位的進位來到時,可以通過一個雙路開關選出輸出結果。這就是進位選擇加法器的思想。提前計算多少位的數據為宜?同為32位的情況:線形進位選擇加法器,方法是分N級,每級計算32/N位;平方根進位選擇加法器,考慮到使兩個路徑
1,提前計算出若干位針對這兩種可能性的結果的路徑,
2,上一位的進位通過前面的結構的路徑的延時達到相等或是近似。
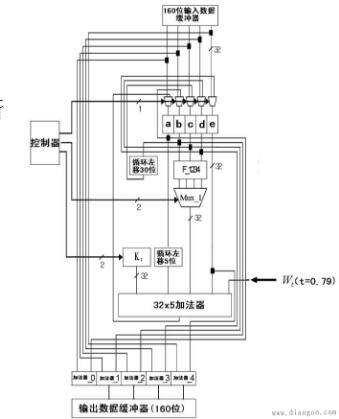
方法,或是2345666即第一級相加2位,第二級3位,第三級4位,第四級5位,第五級6位,第六級6位,第七級6位;或是345677即第一級相加3位,第二級4位,第三級5位,第四級6位,第五級7位,第六級7位。進一步分析加法進行的機制,可以使加法器的結構進一步并行化。令G=AB,P=A⊕B,則COUT(G,P)=G+PCIN,S(G,P)=P⊕CIN。由此,A,B,CIN,S,COUT五者的關系,變為了G,P,CIN,S,COUT五者的關系。再定義點運算(*),(G,P)*(G’,P’)=(G+PG’,PP’),可以分解(G3:2,P3:2)=(G3,P3)(G2,P2)。
點運算服從結合律,但不符合交換律。點運算只與G,P有關而與CIN無關,也就是可以通過只對前面若干位G,P進行點運算計算,就能得到第N位的GN:M,PN:M值,當取M為0時,獲得的GN:0,PN:0即可與初使的CIN一起代入COUT(G,P)=G+PCIN,S(G,P)=P⊕CIN,得到此位的COUT,S;而每一位的G,P值又只與該位的A,B值即輸入值有關,所以在開始進行運算后,就能并行的得到每一位的G,P值。以上分析產生了超前進位加法器的思想:三步運算,1,由輸入的A,B算出每一位的G,P;2,由各位的G,P算出每一位的GN:0,PN:0;3,由每一位的GN:0,PN:0與CIN算出每一位的COUT,S。其中第1,3步顯然是可以并行處理的,計算的主要復雜度集中在了第2步。第2步的并行化,也就是實現GN:0,PN:0的點運算分解的并行化。
加法器的優化設計
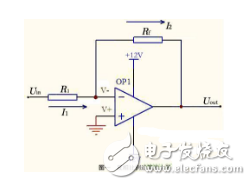
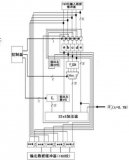
邏輯改造后,電路也應該相應地進行優化設計,因為如果用普通的門電路來實現式(12)~(15)的邏輯,晶體管數目(面積)會增加。另外,在電路級也可以采用減少節點翻轉和寄生電容的方法來降低功耗。式(12)~(15)中多處要用到同或門,設計中,我們用基于旁路的靜態邏輯實現產生gs的同或門,如圖2。旁路邏輯通過由附加管形成的旁路,可以把“串并交錯”的電路結構簡化為單一的串或者并的形式。它的電路和版圖都有很好的規整性,并且可以減小寄生電容。是兩種同或門N塊版圖不同部分的比較,(b)是基于旁路邏輯實現的,與(a)相比,少了一條金屬連線和兩個金屬接觸,使版圖變得十分規整,擴散區不會被隔斷。
在拓撲上,兩條分支用公共的漏區,達到最少的接觸孔和金屬互連,比“串并”和“并串”的晶體管配置方式規整,且寄生電容小。加法器電路上的延遲值旁路邏輯不能實現傳輸門,因而不能用傳輸門實現同或和異或,但是容易證明,三態門在速度和功耗方面都比傳輸門優越。
參照傳輸門的結合方式,我們用兩個三態反相器和一個反相器實現了同或門。實現了式(13)括號內的兩個同或邏輯,平均只需要1級門延時,而用普通門實現的“與非或與非”形式的同或門需要2級或3級門延時。由上面的同或門設計得到啟發,根據形如式(13)的邏輯,設計了一個10管單元utiandor2。
該單元電路實現s=c0CK+0CKN,只要把式(12)~(15)中的括號部分從CK和CKN輸入,輸出就相應得到了s0~s3。僅當CKN=時,電路(a)兩邊均是三態反相器,構成圖5(b)的同或門,兩個反相器交替導通,s=c0⊙CK;當CKN=CK(發生幾率比較大),左邊P管和右邊N管,或者左邊N管和右邊P管交替導通,輸出s=CK,從而屏蔽了c0的變化。考察第一組4位CLA中的進位產生邏輯最復雜的s3,參考式(15),當g2,g1,g0均為0,p2,p1,p0均為1時,s3=gs3⊙c0,顯然這是一種特殊情況,即低位各位都不產生進位,但可以傳遞進位時,直接把c0傳至高位與gs同或即可產生和。c0在各位和生成邏輯的最后一級才加入,可以消除過早加入帶來的不必要的翻轉。左右兩塊交替導通,只存在下拉或上拉延時,有類似動態電路延遲小的優點。僅用了10個晶體管,比常規門實現的積之和節省8個。
?
加法器的類型
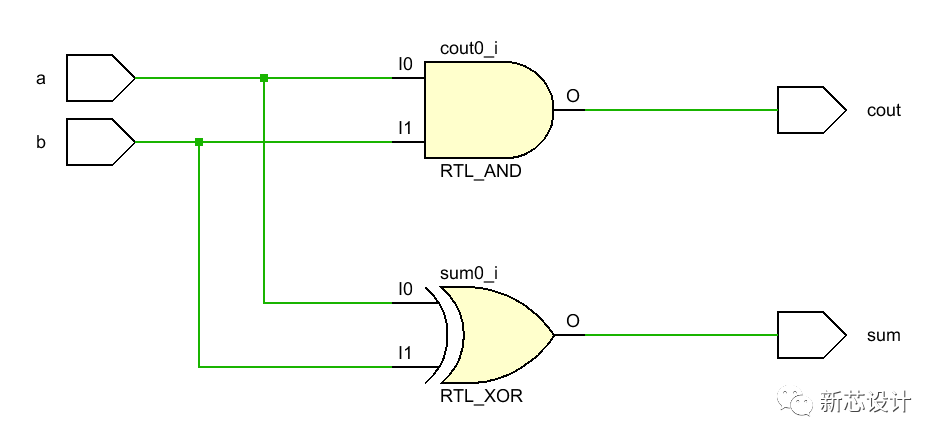
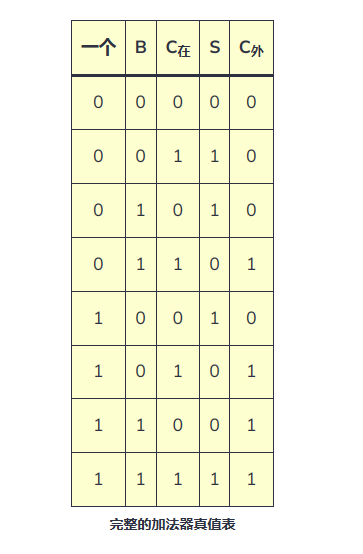
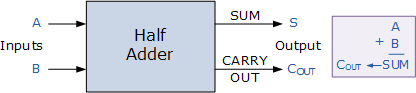
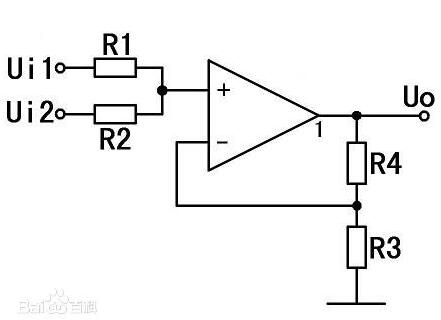
全加器引入了進制值的輸入,以計算較大的數。為區分全加器的兩個進制線,在輸入端的記作Ci或Cin,在輸出端的則記作Co或Cout。半加器簡寫為H.A.,全加器簡寫為F.A.。半加器:半加器的電路圖半加器有兩個二進制的輸入,其將輸入的值相加,并輸出結果到和(Sum)和進制(Carry)。半加器雖能產生進制值,但半加器本身并不能處理進制值。全加器:全加器三個二進制的輸入,其中一個是進制值的輸入,所以全加器可以處理進制值。全加器可以用兩個半加器組合而成。
 電子發燒友App
電子發燒友App










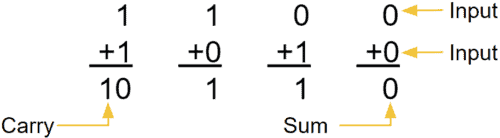














評論