標(biāo)準(zhǔn)形式邏輯函數(shù)
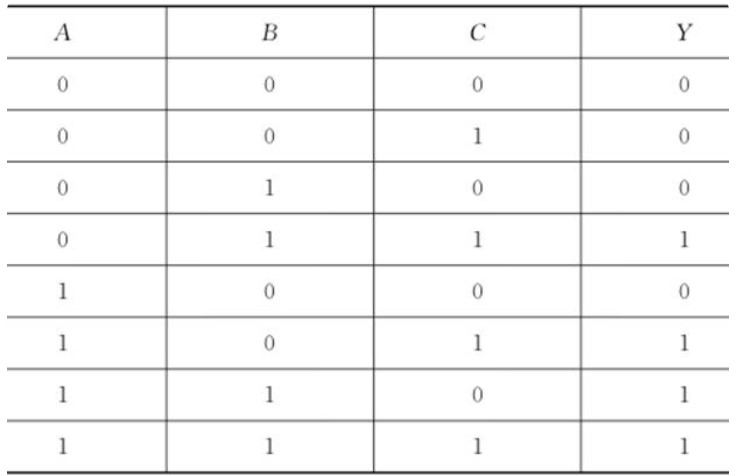
為什么稱該與項(xiàng)為最小項(xiàng)呢?下表列出了3變量的邏輯函數(shù),其共有8個(gè)最小項(xiàng),在自變量的8種取值的組合中,任一最小項(xiàng)為1的機(jī)會(huì)僅一次,其余皆為0,故稱其為最小項(xiàng)。
上表中列出了3變量的邏輯函數(shù)的最小項(xiàng),但其在書寫時(shí)比較麻煩,通常使用簡(jiǎn)化的表示方法,用m0,m1,m2,m3,m4,m5,m6,m7分別表示:
。m的下標(biāo)實(shí)際上是該與項(xiàng)將其原變量用1、反變量用0代入,將其對(duì)應(yīng)的二進(jìn)制數(shù)轉(zhuǎn)換為十進(jìn)制數(shù)得到的。至于四變量、五變量或二變量的最小項(xiàng)同理可得。
邏輯函數(shù)的與或表達(dá)式中每個(gè)與項(xiàng)都由最小項(xiàng)式,那么如何得到最小項(xiàng)表達(dá)式,通常有兩種情況得到:一種是由一般與或表達(dá)式得到最小項(xiàng)表達(dá)式;另一種是由真值表得到。
(1)一般與或表達(dá)式得到最小項(xiàng)表達(dá)式
從一般與或表達(dá)式得到最小項(xiàng)表達(dá)式只須將每個(gè)與項(xiàng)乘上未出現(xiàn)的變量的原變量與反變量和的形式,展開后即得到最小項(xiàng)表達(dá)式。
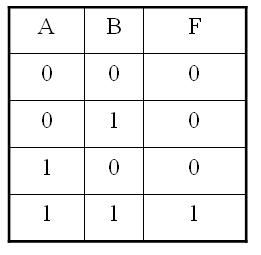
例 寫出F=AB+BC+AC的最小項(xiàng)表達(dá)式。
(1)一般與或表達(dá)式得到最小項(xiàng)表達(dá)式
從一般與或表達(dá)式得到最小項(xiàng)表達(dá)式只須將每個(gè)與項(xiàng)乘上未出現(xiàn)的變量的原變量與反變量和的形式,展開后即得到最小項(xiàng)表達(dá)式。
例 寫出F=AB+BC+AC的最小項(xiàng)表達(dá)式。
由真值表得到最小項(xiàng)表達(dá)式只須首先找出使邏輯函數(shù)F為1的變量組合項(xiàng)的最小項(xiàng),再將這些最小項(xiàng)相或,即得到標(biāo)準(zhǔn)與或表達(dá)式(或最小項(xiàng)表達(dá)式)。
例 寫出下真值表對(duì)應(yīng)的最小項(xiàng)表達(dá)式。
例 寫出下真值表對(duì)應(yīng)的最小項(xiàng)表達(dá)式。
|
輸入變量 |
輸出 |
最小項(xiàng) | ||
|
A |
B |
C |
F | |
|
0 |
0 |
0 |
1 |
m0 |
|
0 |
0 |
1 |
1 |
m1 |
|
0 |
1 |
0 |
0 |
m2 |
|
0 |
1 |
1 |
0 |
m3 |
|
1 |
0 |
0 |
1 |
m4 |
|
1 |
0 |
1 |
1 |
m5 |
|
1 |
1 |
0 |
1 |
m6 |
|
1 |
1 |
1 |
0 |
m7 |
F(A,B,C)=m0+m1+m4+m5+m6=∑m(0,1,4,5,6)
邏輯函數(shù)的標(biāo)準(zhǔn)或與表達(dá)式
為什么稱該或項(xiàng)為最大項(xiàng)呢?下表列出了3變量的邏輯函數(shù),其共有8個(gè)最大項(xiàng),在自變量的8種取值的組合中,任一最大項(xiàng)為0的機(jī)會(huì)僅一次,其余皆為1,故稱其為最大項(xiàng)。
例 寫出函數(shù)F(A,B,C)=∑m(1,3,6,7)的最大項(xiàng)。
|
輸入變量 |
輸出變量 |
最小項(xiàng) |
最大項(xiàng) | ||
|
A |
B |
C |
F | ||
|
0 |
0 |
0 |
0 |
m0 |
M0 |
|
0 |
0 |
1 |
1 |
m1 |
M1 |
|
0 |
1 |
0 |
0 |
m2 |
M2 |
|
0 |
1 |
1 |
1 |
m3 |
M3 |
|
1 |
0 |
0 |
0 |
m4 |
M4 |
|
1 |
0 |
1 |
0 |
m5 |
M5 |
|
1 |
1 |
0 |
1 |
m6 |
M6 |
|
1 |
1 |
1 |
1 |
m7 |
M7 |
例 已知函數(shù)F(A,B,C)=AB+BC,試寫出其最大項(xiàng)表達(dá)式。
從上表可以看出,只須將該函數(shù)的真值表列出,將F為0對(duì)應(yīng)的最大項(xiàng)寫出來即可以了。
從上表可以看出,只須將該函數(shù)的真值表列出,將F為0對(duì)應(yīng)的最大項(xiàng)寫出來即可以了。
|
輸入變量 |
輸出變量 |
最小項(xiàng) |
最大項(xiàng) | ||
|
A |
B |
C |
F | ||
|
0 |
0 |
0 |
0 |
m0 |
M0 |
|
0 |
0 |
1 |
0 |
m1 |
M1 |
|
0 |
1 |
0 |
0 |
m2 |
M2 |
|
0 |
1 |
1 |
1 |
m3 |
M3 |
|
1 |
0 |
0 |
0 |
m4 |
M4 |
|
1 |
0 |
1 |
0 |
m5 |
M5 |
|
1 |
1 |
0 |
1 |
m6 |
M6 |
|
1 |
1 |
1 |
1 |
m7 |
M7 |
F(A,B,C)=∏M(0,1,2,4,5)
- 邏輯函數(shù)(9420)
相關(guān)推薦
Python的函數(shù)式編程介紹
函數(shù) 回顧一下函數(shù),函數(shù)就是把固定的邏輯放在一起,方便我們下次使用,不用寫重復(fù)的代碼,提升代碼的復(fù)用性以及可讀性;一個(gè)好的函數(shù),可以只通過函數(shù)名就可以看懂這個(gè)過程要做什么,所以當(dāng)我們有很大一段邏輯
2023-09-27 16:54:02 650
650
 650
650邏輯函數(shù)與邏輯問題的介紹
本帖最后由 gk320830 于 2015-3-9 22:17 編輯
邏輯函數(shù)與邏輯問題的描述 在討論了與、或、非三種基本邏輯運(yùn)算后,下面將從工程實(shí)際出發(fā),提出邏輯命題,然后用真值表加以描述
2009-04-06 23:57:10
函數(shù)的參數(shù)
對(duì)比功能塊,函數(shù)沒有任何他們保存參數(shù)值的內(nèi)存。在函數(shù)激活時(shí),本地?cái)?shù)據(jù)只中臨時(shí)地貯存。由于這個(gè)原因,當(dāng)調(diào)用函數(shù)時(shí),所有在函數(shù)聲明部分定義的形式輸入、輸入/輸出和輸出參數(shù)必須賦予實(shí)際參數(shù)。
2023-04-27 15:26:26 252
252
 252
252
利用74LS138實(shí)現(xiàn)邏輯函數(shù)式Y(jié)的邏輯功能
例題:利用74LS138實(shí)現(xiàn)邏輯函數(shù)式Y(jié)的邏輯功能。
2023-03-23 14:38:04 8270
8270
 8270
8270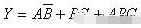
C語言函數(shù)調(diào)用的形式及過程
C語言函數(shù)調(diào)用時(shí)的數(shù)據(jù)傳遞
在調(diào)用有參函數(shù)時(shí),主調(diào)函數(shù)和被調(diào)函數(shù)之間有數(shù)據(jù)傳遞關(guān)系。
在定義函數(shù)時(shí)函數(shù)名后面括號(hào)中的變量稱為“形式參數(shù)”或“虛擬參數(shù)”;在主調(diào)函數(shù)中調(diào)用一個(gè)函數(shù)時(shí),函數(shù)名后面括號(hào)中的參數(shù)稱為“實(shí)際參數(shù)”。
2023-03-10 14:28:25 595
595
 595
595函數(shù)與遞歸-1
在我看來,如果說各種循環(huán)與分支是一個(gè)系統(tǒng)的骨架的話,那么形式繁多的函數(shù)就是C語言的血肉了,正是各式各樣的函數(shù)決定了C語言的各種功能。那么話不多說,既然函數(shù)如此重要,那就快跟我一起了解函數(shù)吧
2023-02-21 15:50:38 218
218
 218
218
標(biāo)準(zhǔn)邏輯和微型邏輯如何實(shí)現(xiàn)創(chuàng)新
的SoC重新設(shè)計(jì)之間擴(kuò)展或修改功能是Nexperia標(biāo)準(zhǔn)邏輯(12引腳或更多)和迷你邏輯(最多10引腳)器件可以發(fā)揮的作用之一。我們的產(chǎn)品解決了大型系統(tǒng)所依賴的許多小問題。
2023-02-10 10:08:41 174
174
 174
174對(duì)于指針類型使用標(biāo)準(zhǔn)庫(kù)函數(shù)
解答: 對(duì)于指針類型,使用下列某個(gè)標(biāo)準(zhǔn)庫(kù)函數(shù): 函數(shù)說明 函數(shù)說明 memcpypgm2ram 將ROM 中的一段緩沖區(qū)復(fù)制到RAM memmovepgm2ram 將ROM 中的一段緩沖區(qū)復(fù)制到
2023-01-22 17:00:00 414
414
 414
414數(shù)字電子技術(shù)基礎(chǔ)----邏輯函數(shù)的化簡(jiǎn)方法
本文通過具體題目來總結(jié)邏輯函數(shù)的化簡(jiǎn)方法。
2022-12-30 14:07:55 4085
4085
 4085
4085使用函數(shù)表示組合邏輯的方法
數(shù)字門級(jí)電路可分為兩大類:組合邏輯和時(shí)序邏輯。鎖存器是組合邏輯和時(shí)序邏輯的一個(gè)交叉點(diǎn),在后面會(huì)作為單獨(dú)的主題處理。
2022-12-21 09:18:32 393
393
 393
393關(guān)于征集《信息安全技術(shù) 散列函數(shù)》系列國(guó)家標(biāo)準(zhǔn)參編單位的通知
關(guān)于征集《信息安全技術(shù) 散列函數(shù) 第1部分 概述》標(biāo)準(zhǔn)參編單位的通知 關(guān)于征集《信息安全技術(shù) 散列函數(shù) 第2部分 采用n位塊密碼的散列函數(shù)》標(biāo)準(zhǔn)參編單位的通知 關(guān)于征集《信息安全技術(shù) 散列函數(shù) 第3部分 專用散列函數(shù)》標(biāo)準(zhǔn)參編單位的通知 來源:全國(guó)信安標(biāo)委
2022-11-15 14:39:19 355
355
 355
355#硬聲創(chuàng)作季 電子技術(shù)基礎(chǔ):44.3邏輯函數(shù)的標(biāo)準(zhǔn)形式及形式變化
電子技術(shù)
Mr_haohao發(fā)布于 2022-11-07 17:06:01


#硬聲創(chuàng)作季 數(shù)字邏輯電路:邏輯函數(shù)表達(dá)式的形式
邏輯電路數(shù)字邏輯數(shù)字邏輯電路
Mr_haohao發(fā)布于 2022-11-04 23:17:19


#硬聲創(chuàng)作季 #數(shù)字電路 數(shù)字電路與邏輯設(shè)計(jì)-2.3.2邏輯表達(dá)式的標(biāo)準(zhǔn)形式-2
標(biāo)準(zhǔn)數(shù)字電路
水管工發(fā)布于 2022-10-28 22:15:23


#硬聲創(chuàng)作季 #數(shù)字電路 數(shù)字電路與邏輯設(shè)計(jì)-2.3.2邏輯表達(dá)式的標(biāo)準(zhǔn)形式-1
標(biāo)準(zhǔn)數(shù)字電路
水管工發(fā)布于 2022-10-28 22:12:14


傳遞函數(shù)的三種形式及應(yīng)用場(chǎng)合
傳遞函數(shù)表示線性定常系統(tǒng)自身,將輸入信號(hào)變換成輸出信號(hào)的能力。這是線性定常系統(tǒng)自身的特點(diǎn),一個(gè)不同的輸入就會(huì)有一個(gè)不同的輸出。輸入信號(hào)本身不影響傳遞函數(shù),傳遞函數(shù)是我這個(gè)系統(tǒng)自身決定的。
2022-10-25 09:27:31 4843
4843
 4843
4843使用SCL語言編寫函數(shù)計(jì)算方差和標(biāo)準(zhǔn)差
方差也稱為“平方差”,用來描述集合中變量的離散程度,即變量與平均值的偏離程度。方差越大,表示變量與平均值的偏離程度越大,即越不穩(wěn)定。標(biāo)準(zhǔn)差是方差的算術(shù)平方根。今天這篇文章,我們就用SCL語言編寫函數(shù)來計(jì)算方差和標(biāo)準(zhǔn)差。
2022-10-17 09:17:45 745
745
 745
745#硬聲創(chuàng)作季 #FPGA FPGA學(xué)數(shù)電-04-邏輯函數(shù)的標(biāo)準(zhǔn)形式與卡諾圖-7
fpga標(biāo)準(zhǔn)數(shù)電數(shù)電基礎(chǔ)
水管工發(fā)布于 2022-10-09 13:33:28

包裝RESTful形式的接口步驟
基于現(xiàn)在微服務(wù)或者服務(wù)化的思想,我們大部分的業(yè)務(wù)邏輯處理函數(shù)都是長(zhǎng)這樣的:
2022-09-22 09:52:36 533
533
 533
533函數(shù)部分定義的形式輸入
調(diào)用之后,函數(shù)的結(jié)果可用作為返回值或作為輸出和輸入/輸出參數(shù)(實(shí)際參數(shù))。
2022-08-02 14:40:55 566
566
 566
566C語言標(biāo)準(zhǔn)庫(kù)函數(shù)
C語言標(biāo)準(zhǔn)庫(kù)函數(shù),使用C語言編程時(shí),常用到的函數(shù)。
2022-05-11 16:41:35 48
48
 48
48什么是位邏輯指令?
作;對(duì)于線圈指令而言,1表示信號(hào)流到達(dá)線圈,O表示信號(hào)流未到達(dá)線圈。 位邏輯指令是plc編程中最基本、使用最頻繁的指令,按不同的功能和用途具有不同的形式,總的來說可以分為下述幾大類:標(biāo)準(zhǔn)位邏輯指令、置位/復(fù)位指令、立即位邏輯指令、其他位邏輯指令。 標(biāo)
2022-02-04 16:22:00 4845
4845
 4845
4845基于標(biāo)準(zhǔn)庫(kù)函數(shù)與基于HAL庫(kù)函數(shù)的stm32編程方式對(duì)比
以實(shí)例程序(串口通信),分析基于標(biāo)準(zhǔn)庫(kù)函數(shù)與基于HAL庫(kù)函數(shù)的stm32編程方式的差異一、基于標(biāo)準(zhǔn)庫(kù)函數(shù)的stm32編程方式二、基于HAL庫(kù)函數(shù)的stm32編程方式差異三、stdunio IDE試玩
2021-12-28 19:09:14 26
26
 26
26stm32下標(biāo)準(zhǔn)庫(kù)函數(shù)與HAL庫(kù)函數(shù)編程方式的差異
stm32下標(biāo)準(zhǔn)庫(kù)函數(shù)與HAL庫(kù)函數(shù)編程方式的差異標(biāo)準(zhǔn)庫(kù)函數(shù)HAL庫(kù)函數(shù)標(biāo)準(zhǔn)庫(kù)函數(shù)與HAL庫(kù)函數(shù)代碼對(duì)比總結(jié)標(biāo)準(zhǔn)庫(kù)函數(shù)由于寄存器開發(fā)難度很大,因此ST公司就專門編寫了芯片的庫(kù)函數(shù)(固件庫(kù)),將一些
2021-12-09 14:21:06 15
15
 15
15STM32 之 標(biāo)準(zhǔn)外設(shè)版USB驅(qū)動(dòng)庫(kù)詳解(架構(gòu)+文件+函數(shù)+使用說明+示例程序)
STM32 之 標(biāo)準(zhǔn)外設(shè)版USB驅(qū)動(dòng)庫(kù)詳解(架構(gòu)+文件+函數(shù)+使用說明+示例程序)
2021-12-08 20:36:09 40
40
 40
40HGP:STM32的用標(biāo)準(zhǔn)庫(kù)函數(shù)自己編寫的關(guān)于設(shè)置系統(tǒng)時(shí)鐘72Mhz的函數(shù)
)//最大計(jì)數(shù)函數(shù),函數(shù)如果計(jì)數(shù)到0x0500000,PLL還未準(zhǔn)備好,那就放棄。ErrorStatus My_WaitPLLStartUp(void);//由于標(biāo)準(zhǔn)庫(kù)沒有等待PLL穩(wěn)定的函數(shù),所以可以自己編寫一個(gè);void Set_SysClock72Mhz(void){uint32_t PLL_SY
2021-11-23 18:21:40 10
10
 10
10傳遞函數(shù)極點(diǎn)和零點(diǎn)的影響是什么
簡(jiǎn)要回顧一些基本概念:傳遞函數(shù)在數(shù)學(xué)上表示濾波器的頻域輸入到輸出行為;可以用變量s來表示傳遞函數(shù),它代表復(fù)雜的頻率,當(dāng)需要計(jì)算特定頻率的幅度和相位響應(yīng)時(shí)可以用jω代替s ;傳遞函數(shù)的標(biāo)準(zhǔn)化形式就像一
2021-06-12 18:05:00 7814
7814
 7814
7814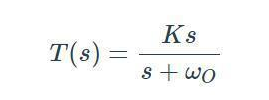
邏輯函數(shù)的定義/表示方法
在邏輯電路中,如果輸入變量A、B、C……的取值確定后,輸出變量Y的值也被唯一確定了,那么就稱Y是A、B、C……的邏輯函數(shù)。
2021-01-31 10:43:07 12754
12754
 12754
12754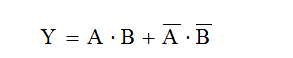
信號(hào)邏輯電平的標(biāo)準(zhǔn)詳細(xì)說明
做SI仿真分析之前,首先需要了解SI問題的基礎(chǔ)理論,掌握SI反射、串?dāng)_、損耗的成因,然后對(duì)于仿真波形需要掌握判斷標(biāo)準(zhǔn),這就需要知曉信號(hào)邏輯電平標(biāo)準(zhǔn)的知識(shí)了。
2021-01-08 16:14:17 0
0
 0
0STM32的標(biāo)準(zhǔn)例程庫(kù)函數(shù)資料合集免費(fèi)下載
本文檔的主要內(nèi)容詳細(xì)介紹的是STM32的標(biāo)準(zhǔn)例程庫(kù)函數(shù)資料合集免費(fèi)下載。
2020-12-28 08:00:00 22
22
 22
22PLC程序設(shè)計(jì)的邏輯方法和步驟
就是應(yīng)用邏輯代數(shù)以邏輯組合的方法和形式設(shè)計(jì)程序。邏輯法的理論基礎(chǔ)是邏輯函數(shù),邏輯函數(shù)就是邏輯運(yùn)算與、或、非的邏輯組合。
2020-06-04 11:49:49 3816
3816
 3816
3816邏輯NOT函數(shù)功能介紹
邏輯NOT函數(shù)輸出在其單個(gè)輸入為false時(shí)為true,在單個(gè)輸入為true時(shí)為false邏輯NOT函數(shù)僅為單個(gè)輸入反相器將邏輯電平“1”的輸入改變?yōu)?b style="color: red">邏輯電平“0”的輸出,反之亦然。
2019-06-23 05:48:00 7846
7846
 7846
7846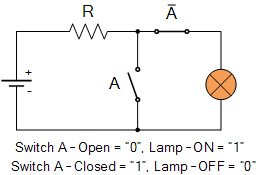
人工智能中的離散數(shù)學(xué)有什么作用詳細(xì)資料介紹
邏輯學(xué):研究人的思維形式和規(guī)律的科學(xué)。由于研究的對(duì)象和方法各有側(cè)重而又分為形式邏輯、辯證邏輯和數(shù)理邏輯。
2018-11-07 10:10:41 23
23
 23
23LUT如何構(gòu)成邏輯函數(shù)
LUT如何如何構(gòu)成邏輯函數(shù);2個(gè)LUT通過互連可以構(gòu)成7bit輸入,單bit輸出的邏輯。實(shí)現(xiàn)方式為兩個(gè)LUT的輸入信號(hào)A1,A2,A3,A4,A5,A6接到一起,輸出信號(hào)經(jīng)過選擇器選擇輸出,選擇器的選擇信號(hào)也是邏輯函數(shù)的一個(gè)輸入信號(hào)。
2018-10-26 14:31:07 9830
9830
 9830
9830c標(biāo)準(zhǔn)庫(kù)函數(shù)大全中文版詳細(xì)資料免費(fèi)下載
本文包括大部分 C 標(biāo)準(zhǔn)庫(kù)函數(shù),但沒有列出一些用途有限的函數(shù)以及某些可以簡(jiǎn)單的從其他函數(shù)合成的函數(shù),也沒有包含多字節(jié)和本地化函數(shù)。
2018-08-14 08:00:00 35
35
 35
35標(biāo)準(zhǔn)IO的操作原理及操作函數(shù)相關(guān)資料下載
標(biāo)準(zhǔn)IO的操作原理及操作函數(shù)相關(guān)資料下載
2018-04-03 16:53:30 4
4
 4
4Oracle中的函數(shù)與表達(dá)式
Oracle中提供了大量的內(nèi)置函數(shù),以處理各種形式的運(yùn)算。這些函數(shù)涵蓋了字符串運(yùn)算、數(shù)值運(yùn)算、日期運(yùn)算等方面。同樣,Oracle允許使用數(shù)值運(yùn)算、邏輯運(yùn)算等基本的表達(dá)式運(yùn)算,另外,提供了SQL標(biāo)準(zhǔn)所規(guī)定的特殊判式。
2018-03-26 16:22:44 17
17
 17
17標(biāo)準(zhǔn)C函數(shù)庫(kù)的用法
C標(biāo)準(zhǔn)函數(shù)庫(kù)是所有符合標(biāo)準(zhǔn)的頭文件的集合,以及常用的函數(shù)庫(kù)實(shí)現(xiàn)程序,例如I/O 輸入輸出和字符串控制。不像 COBOL、Fortran 和 PL/I等編程語言,在 C 語言的工作任務(wù)里不會(huì)包含嵌入的關(guān)鍵字。
2018-03-02 11:27:08 4657
4657
 4657
4657
標(biāo)準(zhǔn)函數(shù)是什么_標(biāo)準(zhǔn)函數(shù)有哪些
在程序設(shè)計(jì)中,常將一些常用的功能模塊編寫成的函數(shù)放在函數(shù)庫(kù)中供公共選用,一般稱為標(biāo)準(zhǔn)函數(shù)。程序是由若干個(gè)程序模塊組成的,高級(jí)語言中有子程序這個(gè)概念,子程序的功能由函數(shù)來實(shí)現(xiàn)的。C++標(biāo)準(zhǔn)函數(shù)庫(kù)為C++程序員們提供了一個(gè)可擴(kuò)展的基礎(chǔ)性框架。
2018-03-02 10:24:23 8538
8538
 8538
8538
基于幾何代數(shù)的高階邏輯形式化建模
計(jì)算和建模分析的傳統(tǒng)方法,如數(shù)值計(jì)算方法和符號(hào)方法等,都存在計(jì)算不精確或者不完備等問題,高階邏輯定理證明是驗(yàn)證系統(tǒng)正確的一種嚴(yán)密的形式化方法.在高階邏輯證明工具HOL-Light中建立了幾何代數(shù)系統(tǒng)的形式化模型,主要包
2018-01-16 18:09:24 0
0
 0
0index函數(shù)語法說明及應(yīng)用實(shí)例
INDEX函數(shù)是返回表或區(qū)域中的值或?qū)χ档囊谩?b style="color: red">函數(shù)INDEX()有兩種形式:數(shù)組形式和引用形式。數(shù)組形式通常返回?cái)?shù)值或數(shù)值數(shù)組;引用形式通常返回引用。返回特定行和列交叉處單元格的引用。
2017-12-08 18:45:31 10548
10548
 10548
10548C語言中形式參數(shù)和實(shí)際參數(shù)的介紹
C語言函數(shù)參數(shù)的傳遞和值返回 實(shí)際程序中,我們經(jīng)常使用到帶參數(shù)有返回值的函數(shù)。 一、函數(shù)參數(shù)傳遞 1.形式參數(shù)和實(shí)際參數(shù) 函數(shù)的調(diào)用值把一些表達(dá)式作為參數(shù)傳遞給函數(shù)。函數(shù)定義中的參數(shù)是形式參數(shù),函數(shù)的調(diào)用者提供給函數(shù)的參數(shù)叫實(shí)際 參數(shù)。在函數(shù)調(diào)用之前,實(shí)際參數(shù)的值將被拷貝到這些形式參數(shù)中。
2017-11-21 11:25:55 6
6
 6
6包含無關(guān)項(xiàng)邏輯函數(shù)的固定極性轉(zhuǎn)換
包含無關(guān)項(xiàng)邏輯函數(shù)的固定極性轉(zhuǎn)換_汪迪生
2017-01-07 15:53:30 0
0
 0
0解析邏輯函數(shù)式的處理
對(duì)數(shù)字電路設(shè)計(jì)中的重要環(huán)節(jié)--邏輯函數(shù)式的處理進(jìn)行了解析。分邏輯函數(shù)式的化簡(jiǎn)、檢查、變換3個(gè)方面作了詳細(xì)探討,且對(duì)每個(gè)方面給出了相應(yīng)的見解,即對(duì)邏輯函數(shù)式的化簡(jiǎn)方面提
2012-09-12 16:44:46 40
40
 40
40降維卡諾圖在邏輯函數(shù)設(shè)計(jì)中的應(yīng)用
給出了由邏輯函數(shù)表達(dá)式直接做降維卡諾圖、用降維卡諾圖化簡(jiǎn)邏輯函數(shù)的具體步驟和方法,并分析了在設(shè)計(jì)組合邏輯電路中,用降維卡諾圖的方法去構(gòu)造相對(duì)應(yīng)的邏輯函數(shù),從而實(shí)現(xiàn)其邏
2012-04-18 15:27:43 44
44
 44
44新型數(shù)字邏輯標(biāo)準(zhǔn)及接口技術(shù)
在現(xiàn)代數(shù)字電路設(shè)計(jì)中,往往需要在同一系統(tǒng)中采用許多不同邏輯標(biāo)準(zhǔn)的器件,許多優(yōu)秀的硬件工程師可以設(shè)計(jì)出非常復(fù)雜的數(shù)字電路,卻經(jīng)常在不同邏輯標(biāo)準(zhǔn)信號(hào)的互連上被搞得焦頭爛額
2011-02-21 15:16:20 19
19
 19
19WinCC標(biāo)準(zhǔn)函數(shù)總結(jié)
該系統(tǒng)包含標(biāo)準(zhǔn)函數(shù)。 可以按需要修改這些函數(shù)。 此外,還可以自己創(chuàng)建標(biāo)準(zhǔn)函數(shù)。
該系統(tǒng)包括一個(gè)標(biāo)準(zhǔn)函數(shù)集。
一、Alarm - 簡(jiǎn)短描述
Alarm
2010-10-09 16:14:14 56
56
 56
56不同類型觸發(fā)器邏輯功能的函數(shù)描述方法
在數(shù)學(xué)上,我們有三種描述函數(shù)的方法:公式、表格和圖形。同樣,我們有三種描述觸發(fā)器邏輯功能的方法,一是特性方程,二是特性表,三是狀態(tài)轉(zhuǎn)換圖【圖4.3.1,4.3.2, 4.3.
2010-08-02 11:35:16 2765
2765
 2765
2765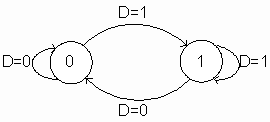
邏輯代數(shù)和函數(shù)化簡(jiǎn)
邏輯代數(shù)和函數(shù)化簡(jiǎn)
2.1 基本邏輯運(yùn)算和復(fù)合邏輯運(yùn)算2.2 邏輯函數(shù)及其描述2.3 邏輯代數(shù)的運(yùn)算法則2.4 邏輯函數(shù)表達(dá)式的形式及其變換2.5 邏輯函數(shù)的
2010-05-26 16:54:11 51
51
 51
51邏輯代數(shù)的化簡(jiǎn)算法
邏輯代數(shù)的化簡(jiǎn)算法
觀察函數(shù)
1.該函數(shù)有四個(gè)邏輯變量,可表示成
Y=f(A、B、C、D)
2
2010-05-25 18:10:45 7682
7682
 7682
7682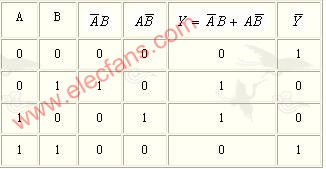
采用表格法化簡(jiǎn)邏輯函數(shù)技術(shù)
采用表格法化簡(jiǎn)邏輯函數(shù)技術(shù)
1、概述
在設(shè)計(jì)邏輯電路圖時(shí),由真值表直接得到的函數(shù)往往比較復(fù)雜。代數(shù)法和卡諾圖法等方法對(duì)于變
2010-05-25 17:51:17 1883
1883
 1883
1883邏輯函數(shù)的公式化簡(jiǎn)法
邏輯函數(shù)的公式化簡(jiǎn)法
一、最簡(jiǎn)標(biāo)準(zhǔn)邏輯函數(shù)式中,包含的或運(yùn)算的項(xiàng)最少;每一項(xiàng)中包含與運(yùn)算的因子最少,二、常用的
2010-02-28 19:03:14 8401
8401
 8401
8401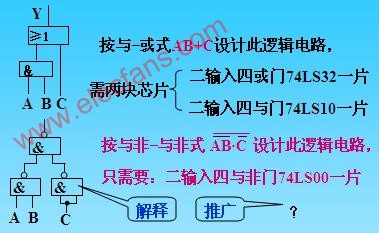
常見邏輯電平標(biāo)準(zhǔn)詳細(xì)介紹
常見邏輯電平標(biāo)準(zhǔn)詳細(xì)介紹
下面總結(jié)一下各電平標(biāo)準(zhǔn)。和新手以及有需要的人共享一下^_^.現(xiàn)在常用的電平標(biāo)準(zhǔn)有TTL、CMOS、LVTTL、LV
2009-11-28 11:26:46 3446
3446
 3446
3446邏輯代數(shù)與邏輯函數(shù)
邏輯代數(shù)與邏輯函數(shù):本章主要討論分析和設(shè)計(jì)數(shù)字邏輯功能的數(shù)學(xué)。首先介紹邏輯代數(shù)中的基本運(yùn)算、基本公式, 常用定理和重要規(guī)則; 然后講述邏輯函數(shù)的形式與轉(zhuǎn)換; 最后介
2009-09-01 09:11:40 47
47
 47
47兩種標(biāo)準(zhǔn)信號(hào)之間的函數(shù)變換
用函數(shù)變換的方法解決兩種標(biāo)準(zhǔn)信號(hào)之間的轉(zhuǎn)換,進(jìn)而闡述了數(shù)學(xué)在解決實(shí)際問題中的應(yīng)用。關(guān)鍵詞:函數(shù)變換、標(biāo)準(zhǔn)信號(hào)。Abstract: This paper resolved the conversion between two st
2009-08-05 08:14:21 8
8
 8
8邏輯代數(shù)基礎(chǔ)
2.1 概述2.2 邏輯函數(shù)及其表示法2.3 邏輯代數(shù)的基本定律和規(guī)則2.4 邏輯函數(shù)的公式化簡(jiǎn)法2.5 邏輯函數(shù)的卡諾圖化簡(jiǎn)法2.2 邏輯函數(shù)及其表示法2.
2009-06-27 09:44:04 29
29
 29
29基于Butterworth標(biāo)準(zhǔn)傳遞函數(shù)設(shè)計(jì)
本文首先給出了Butterworth 標(biāo)準(zhǔn)傳遞函數(shù),然后提出了一種設(shè)計(jì)狀態(tài)反饋系統(tǒng)的方法,該方法包括:利用線性變換將能控系統(tǒng)化為能控標(biāo)準(zhǔn)形,使能控標(biāo)準(zhǔn)形系統(tǒng)的閉環(huán)傳遞函數(shù)等
2009-06-11 09:45:39 18
18
 18
18邏輯函數(shù)的卡諾圖化簡(jiǎn)法
邏輯函數(shù)的卡諾圖化簡(jiǎn)法
由前面的學(xué)習(xí)得知,利用代數(shù)法可以使邏輯函數(shù)變成較簡(jiǎn)單的形式。但要求熟練掌握邏輯代數(shù)的基本定律,而且需要一些技巧,特別是經(jīng)化
2009-04-07 10:11:30 33523
33523
 33523
33523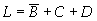
邏輯函數(shù)與邏輯問題的描述
邏輯函數(shù)與邏輯問題的描述
在討論了與、或、非三種基本邏輯運(yùn)算后,下面將從工程實(shí)際出發(fā),提出邏輯命題,然后用真值表加以描述,從真值表可以寫出邏輯函數(shù)。一
2009-04-06 23:56:35 1192
1192
 1192
1192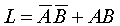
第五講 邏輯函數(shù)的卡諾圖化簡(jiǎn)法
第五講 邏輯函數(shù)的卡諾圖化簡(jiǎn)法
2.5 邏輯函數(shù)的卡諾圖化簡(jiǎn)法2. 5. 1 最小項(xiàng)與卡諾圖一、最小項(xiàng)的定義和性質(zhì)1.最小項(xiàng)的定
2009-03-30 16:03:47 5545
5545
 5545
5545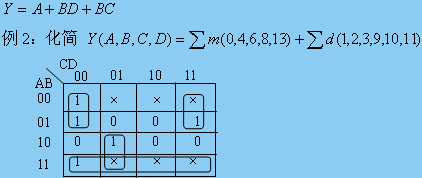
第四講 邏輯函數(shù)的公式化簡(jiǎn)法
第四講 邏輯函數(shù)的公式化簡(jiǎn)法
2 . 4 . 1 化簡(jiǎn)的意義與標(biāo)準(zhǔn)一、化簡(jiǎn)邏輯函數(shù)的意義二、邏輯函數(shù)式的幾種常見形式和變換三、邏
2009-03-30 16:03:02 4833
4833
 4833
4833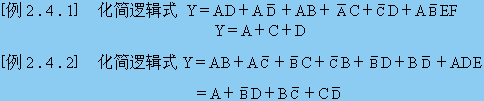
第二講 邏輯代數(shù)基礎(chǔ)
第二講 邏輯代數(shù)基礎(chǔ)2.1 概述2.2邏輯函數(shù)及其表示法2 . 2 . 1 基本邏輯函數(shù)及運(yùn)算一、與邏輯二、或邏輯三、邏輯非2.2.2 幾種導(dǎo)出的邏輯運(yùn)
2009-03-30 16:00:23 943
943
 943
943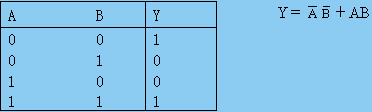
數(shù)字邏輯電路
數(shù)字邏輯電路的內(nèi)容:數(shù)制與編碼,,邏輯代數(shù)和邏輯函數(shù),集成邏輯門,組合邏輯電路,中規(guī)模集成組
2008-09-06 01:54:26 22
22
 22
22matlab邏輯函數(shù)
matlab邏輯函數(shù)
all :向量中是否所有分量均非零 any :是否有元素非零 exist :指定變量或文件是否存在 find :返回矩陣中非零元素的索引
2008-06-18 14:46:23 1329
1329
 1329
1329 電子發(fā)燒友App
電子發(fā)燒友App






















評(píng)論