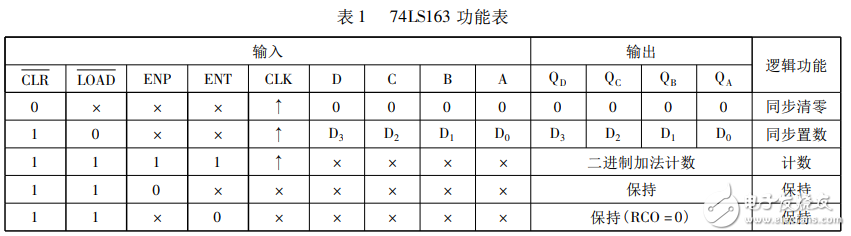
74ls163實現(xiàn)十進制計數(shù)器電路（一）

改變74LS163二進制計數(shù)器為十進制計數(shù)器

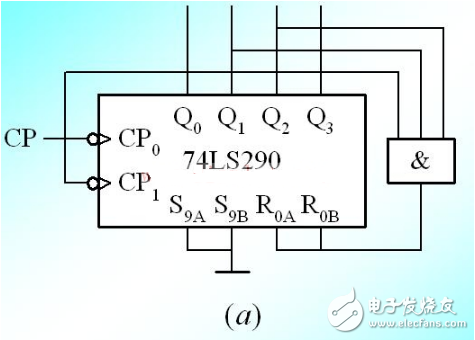
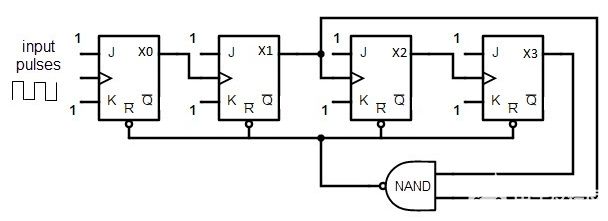
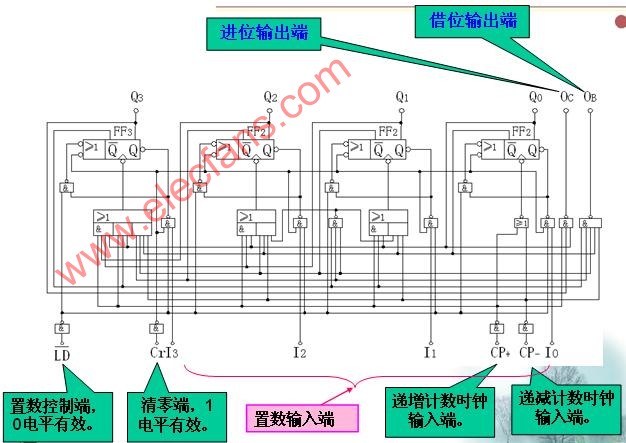
連接電路圖如圖22.2所示，即用一FDS4435BZ個與非門，其兩個輸人取自QA和QD，輸出接清零端α‘R。當?shù)?個脈沖結束時，鈑和QD都為“1”，則與非門輸出為低電平“O”，并加到αR端，因CIR為同步清零端，此時雖已建立清零信號，但并不執(zhí)行清零，只有第1O個時鐘脈沖到來后74LS163才被清零，這就是同步清零的意義所在。

驗證圖是否如同一個模10計數(shù)器：

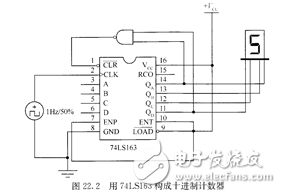
圖 用74I’s163構成十進制計數(shù)器

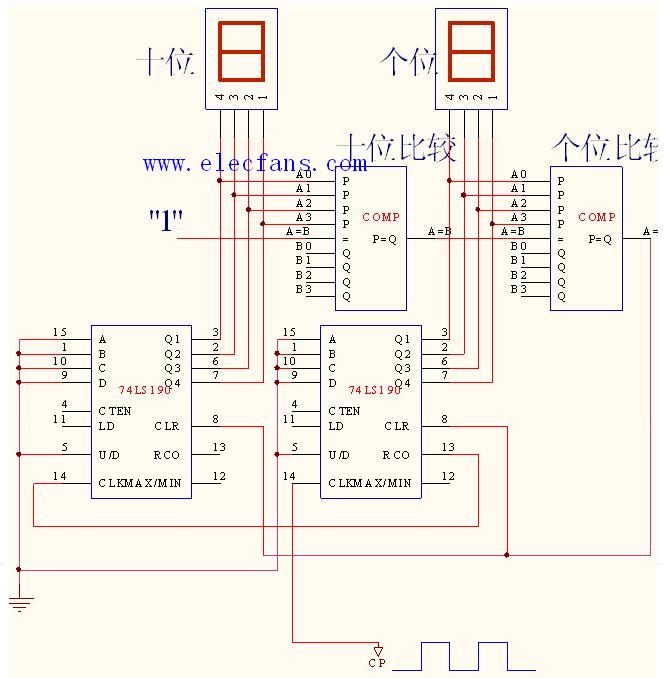
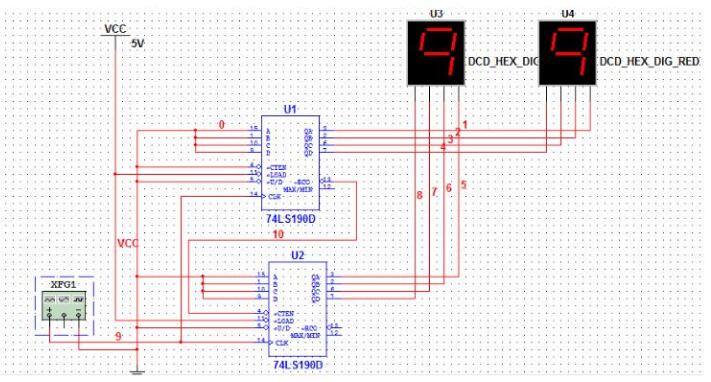
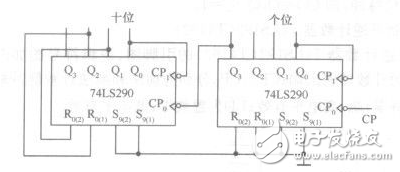
用兩個74ls163連接成一個兩位十進制計數(shù)器。連接電路圖如圖22.3所示。

當74LS163（1）記到9時（1001），產(chǎn)生清零信號并同時使74LS163（2）的控制端ENT為高電平，即使忽s163（2）開始計數(shù)，同樣記到9時（1001）產(chǎn)生低電平清零信號使其清零，輸出顯示為0，并同時產(chǎn)生一進位信號（【D為高電平），可將此信號加到一發(fā)光二極管顯示其進位輸出。計數(shù)器的4位輸出可連接到實驗箱上的譯碼顯示器的4個輸人端，電路如圖22.3所示（注意，計數(shù)器的QA~QD和譯碼器的輸人端A~B一一對應連接）。

74ls163實現(xiàn)十進制計數(shù)器電路（二）

以74LS163為基礎設計一個6分頻電路

首先，需要明白什么叫分頻，圖3展示了分頻的效果：

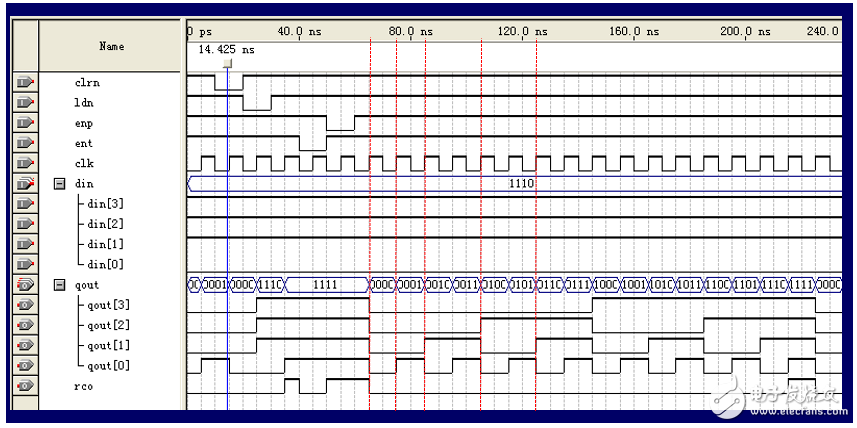
分頻通常以CP（時鐘脈沖）為基礎，從圖3中可以看出：qout［0］的周期為CP的2倍，qout［1］的周期為CP的4倍，qout［2］位8倍，qout［3］為16倍，顯然，其頻率分別為CP的1/2， 1/4， 1/8， 1/16，即所謂的2-分頻，4-分頻，8-分頻，16-分頻。

再進一步分析，對于qout［0］，其變化為：當一個時鐘脈沖來臨時，qout［0］變化一次；對于qout［1］，每兩個時鐘脈沖，qout［1］值變化一次；對于qout［2］，每四個時鐘脈沖，qout［2］值變化一次；對于qout［3］，每8個時鐘脈沖，qout［3］值變化一次。依次類推，如果要做6分頻，顯然應該是每3個時鐘脈沖，值變化一次，如何用74LS163來做6-分頻呢？

顯然，這個問題變?yōu)椋喝绾问?4LS163中的某一位每3個時鐘脈沖跳變一次。顯然，只有QD和QC這兩位的變化可能滿足（QB每兩個脈沖跳變一次，QA每個脈沖跳變一次），如果選擇QC，顯然可以找出一個序列：

0000 —》 0001 —》 0010 —》 1101 —》 1110 —》1111 —》0000 —》 …

對于QC，先是3個0，然后是3個1，開始循環(huán)，正好是6分頻。仔細觀察，發(fā)現(xiàn)這個循環(huán)對于QD也是6分頻。

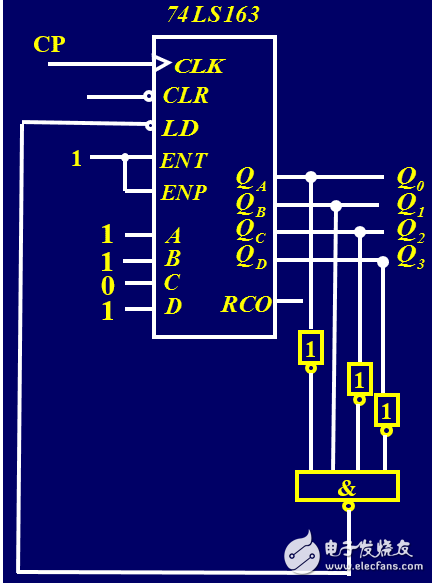
針對上面分析得到的狀態(tài)遷移序列，如何用74LS163來實現(xiàn)呢？對于前半部0000 —》 0001 —》 0010，執(zhí)行的是正常的計數(shù)功能，對于后半部1101 —》 1110 —》1111（ —》0000），執(zhí)行的也是正常的計數(shù)功能，只有0010 —》 1101是一個跳躍，即當計數(shù)器狀態(tài)為0010時，下一個狀態(tài)需要用到163計數(shù)器的并行置數(shù)功能，因此，需要對163的計數(shù)器的輸出進行判斷，當輸出為0010時，用1101對電路進行置數(shù)（確保下一時刻電路狀態(tài)為1101）。

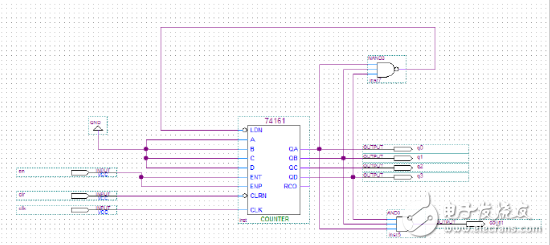
在此分析的基礎上，其電路圖如圖4所示：