Star-Delta轉(zhuǎn)換和Delta-Star轉(zhuǎn)換允許我們將三相配置中連接在一起的阻抗從一種類型的連接轉(zhuǎn)換為另一種類型
我們現(xiàn)在可以解決簡(jiǎn)單的并聯(lián)系列或者橋式電阻網(wǎng)絡(luò)使用基爾霍夫電路定律,網(wǎng)格電流分析或節(jié)點(diǎn)電壓分析技術(shù),但在平衡的三相電路中,我們可以使用不同的數(shù)學(xué)技術(shù)來(lái)簡(jiǎn)化電路分析,從而減少所涉及的數(shù)學(xué)量本身是一件好事。
標(biāo)準(zhǔn)三相電路或網(wǎng)絡(luò)采用兩種主要形式,其名稱代表電阻的連接方式,Star連接網(wǎng)絡(luò)它具有字母符號(hào), Y (Y形)和Delta連接網(wǎng)絡(luò),其符號(hào)為三角形,Δ(delta) 。
如果在一種配置中連接3相,3線電源或甚至3相負(fù)載,它可以是ea通過(guò)使用星形三角洲轉(zhuǎn)換或Delta Star轉(zhuǎn)換過(guò)程,將其轉(zhuǎn)換或改變?yōu)榱硪环N類型的等效配置。
電阻網(wǎng)絡(luò)由三個(gè)阻抗組成可以連接在一起形成 T 或“Tee”配置,但也可以重新繪制網(wǎng)絡(luò)以形成星或Υ鍵入網(wǎng)絡(luò)如下所示。
T型連接和等效星形網(wǎng)絡(luò)
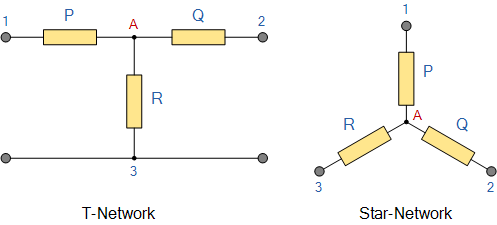
正如我們已經(jīng)看到的,我們可以重新繪制上面的 T 電阻網(wǎng)絡(luò),以生成電氣等效的Star或 Y 型網(wǎng)絡(luò)。但我們也可以將 Pi 或π型電阻網(wǎng)絡(luò)轉(zhuǎn)換為電等效Delta或Δ型網(wǎng)絡(luò)。如下所示。
Pi連接和等效Delta網(wǎng)絡(luò)

現(xiàn)已確切定義什么是星和Delta連接的網(wǎng)絡(luò),可以將 Y 轉(zhuǎn)換為等效的Δ電路,還可以使用轉(zhuǎn)換過(guò)程將Δ轉(zhuǎn)換為等效的 Y 電路。
此過(guò)程允許我們?cè)诟鞣N電阻之間產(chǎn)生數(shù)學(xué)關(guān)系我們一個(gè)星三角變換以及Delta Star變換。
這些電路變換允許我們改變?nèi)齻€(gè)連接的電阻(或阻抗)對(duì)于星形或三角形連接電路,在端子 1-2,1-3 或 2-3 之間測(cè)量它們的等效值。然而,由此產(chǎn)生的網(wǎng)絡(luò)僅相當(dāng)于星形或三角形網(wǎng)絡(luò)外部的電壓和電流,因?yàn)閮?nèi)部電壓和電流不同,但每個(gè)網(wǎng)絡(luò)將消耗相同的功率并且彼此具有相同的功率因數(shù)。
Delta Star Transformation
要將delta網(wǎng)絡(luò)轉(zhuǎn)換為等效的星形網(wǎng)絡(luò),我們需要推導(dǎo)出一個(gè)轉(zhuǎn)換公式,用于在各個(gè)終端之間將各種電阻相互等同。考慮下面的電路。
Delta到Star Network

比較終端之間的電阻 1 和 2 。
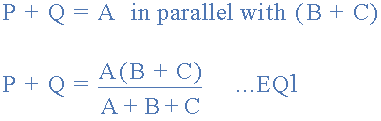
終端之間的電阻 2 和 3 。

終端 1 和之間的電阻3 。
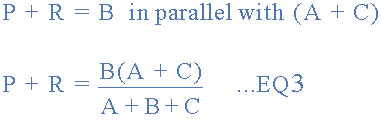
現(xiàn)在給出了三個(gè)方程式,并從等式2中得出方程式3:
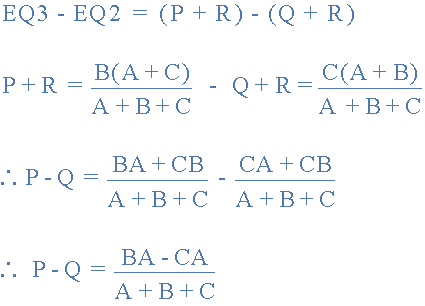
然后,重寫等式1將給我們:

加在一起等式1和等式3的結(jié)果減去等式2給出:
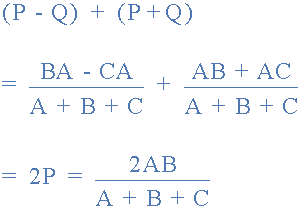
從中給出了電阻 P 的最終等式:
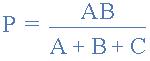
然后總結(jié)一下上面的數(shù)學(xué),我們現(xiàn)在可以說(shuō)星形網(wǎng)絡(luò)中的電阻 P 可以找到等式1加(等式3減去等式2)或 Eq1 +( Eq3 - Eq2)。
類似地,為了在星形網(wǎng)絡(luò)中找到電阻 Q ,等式2加上等式1的結(jié)果減去等式3或 Eq2 +(Eq1 - Eq3)這使我們將 Q 轉(zhuǎn)換為:
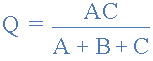
再次,在星形網(wǎng)絡(luò)中找到電阻 R ,等式3加上等式2減去等式1或 Eq3 +(Eq2 - Eq1)的結(jié)果,這給了我們 R 的轉(zhuǎn)換為:
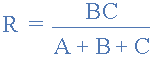
將三角洲網(wǎng)絡(luò)轉(zhuǎn)換為星形網(wǎng)絡(luò)時(shí),所有的分母都是轉(zhuǎn)換公式是相同的: A + B + C ,它是所有delta電阻的總和。然后,為了將任何三角洲連接的網(wǎng)絡(luò)轉(zhuǎn)換為等效的星形網(wǎng)絡(luò),我們可以將上述轉(zhuǎn)換方程概括為:
Delta to Star Transformations Equations
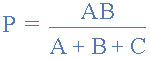
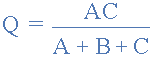
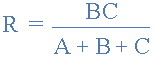
如果三角網(wǎng)絡(luò)中的三個(gè)電阻器的值都相等,則等效星形網(wǎng)絡(luò)中的合成電阻器將等于三角形電阻值的三分之一。這為星形網(wǎng)絡(luò)中的每個(gè)電阻分支提供了以下值: R STAR = 1/3 * R DELTA ,這與說(shuō): (R DELTA )/ 3
Delta - Star示例No1
將以下Delta電阻網(wǎng)絡(luò)轉(zhuǎn)換為等效的星形網(wǎng)絡(luò)。

Star Delta轉(zhuǎn)換
Star Delta轉(zhuǎn)換與上述相反。我們已經(jīng)看到,當(dāng)從三角網(wǎng)絡(luò)轉(zhuǎn)換到等效星形網(wǎng)絡(luò)時(shí),連接到一個(gè)端子的電阻器是連接到同一端子的兩個(gè)三角形電阻的乘積,例如電阻器 P 是產(chǎn)品連接到端子1的電阻器 A 和 B 。
通過(guò)重寫先前的公式,我們還可以找到轉(zhuǎn)換電阻星的轉(zhuǎn)換公式網(wǎng)絡(luò)到等效的三角洲網(wǎng)絡(luò),為我們提供了一種產(chǎn)生星形三角形變換的方法,如下所示。
星形到三角形的轉(zhuǎn)換
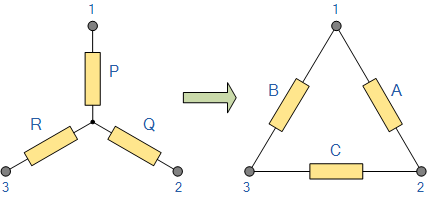
三角形任何一側(cè)的電阻值Δ網(wǎng)絡(luò)是星形網(wǎng)絡(luò)中所有雙電阻組合的總和除以“直接相對(duì)的星形電阻” “找到了三角形電阻器。例如,電阻 A 的格式為:
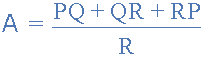
關(guān)于端子3和電阻 B 給出:
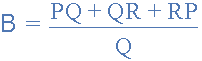
關(guān)于端子2,電阻 C 給定為:

關(guān)于終端1。
通過(guò)將每個(gè)等式除以分母的值,我們最終得到三個(gè)單獨(dú)的轉(zhuǎn)換可用于將任何三角形電阻網(wǎng)絡(luò)轉(zhuǎn)換為等效星形網(wǎng)絡(luò)的公式,如下所示。
星三角形變換方程
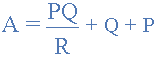
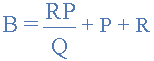

關(guān)于將星形電阻網(wǎng)絡(luò)轉(zhuǎn)換為等效三角網(wǎng)絡(luò)的最后一點(diǎn)。如果星形網(wǎng)絡(luò)中的所有電阻器的值都相等,則等效三角形網(wǎng)絡(luò)中的合成電阻器將是星形電阻器的三倍,并且相等,給出: R DELTA = 3 * R STAR
Star - Delta示例No2
將以下Star Resistive Network轉(zhuǎn)換為等效的Delta網(wǎng)絡(luò)。
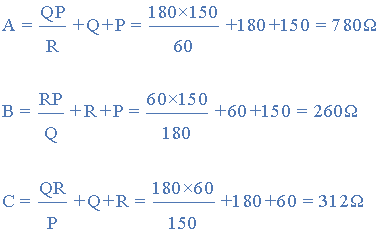
星際轉(zhuǎn)型和Delta Star Transformation允許我們將一種類型的電路連接轉(zhuǎn)換為另一種類型,以便我們輕松分析電路。這些變換技術(shù)可用于對(duì)包含電阻或阻抗的星形或三角形電路產(chǎn)生良好效果。
-
三相
+關(guān)注
關(guān)注
6文章
385瀏覽量
33210 -
星三角
+關(guān)注
關(guān)注
18文章
73瀏覽量
16207
發(fā)布評(píng)論請(qǐng)先 登錄
星三角啟動(dòng)電路圖工作原理和星三角啟動(dòng)電路實(shí)物接線講解

空氣延時(shí)觸頭星三角降壓?jiǎn)?dòng)#星三角形降壓?jiǎn)?dòng)

手動(dòng)星三角降壓?jiǎn)?dòng)#星三角形降壓?jiǎn)?dòng)

星三角正反轉(zhuǎn)降壓?jiǎn)?dòng)控制回路#星三角正反轉(zhuǎn)
電機(jī)星三角降壓?jiǎn)?dòng)接線方法圖解
直流電路中星三角轉(zhuǎn)換分析
電機(jī)的星三角起動(dòng)方式及調(diào)試方法
星三角起動(dòng)方式的優(yōu)點(diǎn)
深度剖析星三角變壓器的相移
星三角啟動(dòng)原理
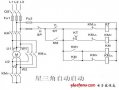
星三角啟動(dòng)電路圖 正反轉(zhuǎn)星三角降壓?jiǎn)?dòng)電路圖
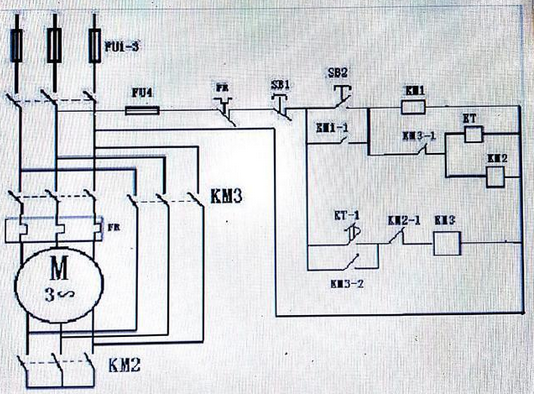





 星三角如何轉(zhuǎn)型?
星三角如何轉(zhuǎn)型?











評(píng)論