四旋翼姿態控制通常選用 PID控制器作為主控環節,但 PID 控制器的參數不易整定,調控結果也存在較大的系統超調量,難以獲得滿意的控制效果。因此設計了 PI-PD 控制器的四旋翼姿態控制方式,其中 PI 控制器能夠使系統快速無穩態誤差的收斂,PD 控制器可以有效的抑制系統超調量。仿真結果表明:PI-PD 控制器能夠很好的抑制系統超調量,縮短系統收斂時間,具有良好的控制效果。
近年來,隨著微型系統、微型傳感器、慣導技術以及飛行控制等技術的發展,四旋翼飛行器(以下簡稱四旋翼)引起了人們的廣泛關注。四旋翼是通過改變四個旋翼的轉速來調整其在空中的飛行姿態,包括俯仰角 θ、橫滾角 φ、偏航角 ψ,從而控制機體水平方向上的運動,因此四旋翼的姿態控制是決定其飛行性能的關鍵所在。在工業過程控制和航空航天控制等領域中,PID 控制的應用達到 80 % 以上,不過由于四旋翼系統的強非線性、慣性和延遲,PID 控制器對四旋翼姿態的調整效果往往出現較多的系統超調量,或者調整時間較長,控制
效果并不令人滿意。因此,設計一種能夠抑制系統超調量,并且保證系統快速收斂的控制器,
可以提高四旋翼系統的穩定性和控制性。
1 PID控制器基本原理
PID 控制器結構簡單、方便調試,廣泛應用于工業生產中。PID 控制器是根據系統輸出的誤差值調節系統輸出的控制形式,包含比例控制(P)、積分控制(I)和微分控制(D),其連續 PID 控制的結構形式為:
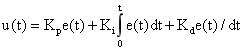
(1)
其中 u(t) 為系統輸出,Kp、Ki、Kd 分別為比例、積分和微分系數,e(t)=y(r)-y(t) 為期望值與輸出量的差值,即輸出誤差。而對于數字控制系統,可將 PID 控制器離散化,得到離散 PID 的結構形式:
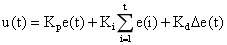 ?(2)
?(2)
其中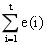 , 為所有誤差值累加之和,Δe(t)=e(t)-e(t-1),等效微分運算。當期望值在相鄰的采樣周期保持不變時,y(r)=y(r-1),Δe(t)=-y(t)+y(t-1),Δe(t) 即為系統輸出的變化量。
, 為所有誤差值累加之和,Δe(t)=e(t)-e(t-1),等效微分運算。當期望值在相鄰的采樣周期保持不變時,y(r)=y(r-1),Δe(t)=-y(t)+y(t-1),Δe(t) 即為系統輸出的變化量。
若基于 PID 控制器來對四旋翼的姿態進行調控,參數整定難度較大,調控效果不佳。鑒于此,本文基于文章 [6] 提出的 PI-PD 控制器,設計了基于 PI-PD 控制器的四旋翼姿態控制方式,用于減小系統超調量,縮短系統收斂時間,提高四旋翼在空中飛行的穩定性和控制性。
2 PI-PD控制器
PID 控制器對于高階時滯系統、復雜的模糊系統以及不確定系統而言,控制效果不佳。而在 PID 控制器基礎上演變而來的 PI-PD 控制器,對于含有積分、振蕩或不穩定環節的控制對象,可以實現較好的閉環控制。PI-PD 控制器其結構圖如圖 1 所示。
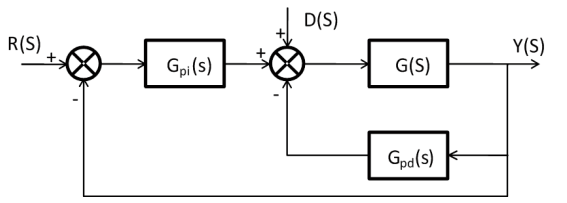
圖 2:PI-PD 控制器等效結構圖
設 PI 控制器和 PD 控制器的傳遞函數為:
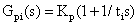 ? ? (3)
? ? (3)
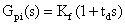 ? ? ?(4)
? ? ?(4)
其中 Kp、Ti 分別 PI 控制器的比例和積分系數,Kf、Td 分別為 PD 控制器的比例和微分系數。圖中,PI 控制器仍處于主控環節上,根據期望值調節輸出量,具有決定系統收斂快慢和消除穩態誤差的作用。而 PD 控制器成為了反饋環節,具有抑制系統振蕩和超調量的作用,并且只與系統輸出變化量有關,與期望值無關。

圖 2:PI-PD 控制器等效結構圖
為了簡化 PI-PD 控制器結構,將其進行結構變換,得到圖 2 所示的等效結構圖。可得到主控環節 PI+PD 控制器為:
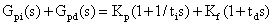 ? ? ?(5)
? ? ?(5)
設 PID 控制器傳遞函數為:
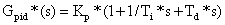 ? ? ? ? ? ?(6)
? ? ? ? ? ?(6)
其中 Kp*、Ti*、Td* 分別為 PID 控制器的參數。于是可將式(5)整理成式(6)的類似形式:
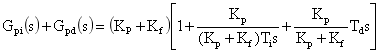
(7)
設 Kp=βKf,參數 β 表示 Kp 與 Kf 的關系,式(7)可變換為:
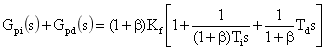
(8)
比較式(6)與式(8),可得出 Kp*、Ti*、Td* 與 Kp、Ti、Kf、Td 之間的關系表達式:
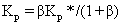 ? (9)
? (9)
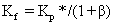 ? (10)
? (10)
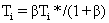 ? ? ?(11)
? ? ?(11)
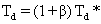 ? ? ? ? (12)
? ? ? ? (12)
根據式(9)和(11)可得:
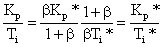 ? ? ? ? (13)
? ? ? ? (13)
根據式(10)和(12)可得:
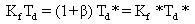 ? ? ? (14)
? ? ? (14)
由此可以看出,根據 PID 控制器的 Kp*參數以及 β 值可以計算出 PI-PD 控制器的 Kp和 Kf 參數,β 決定了 Kp 與 Kf 的分配比例。式(13)和(14)表明,PI-PD 控制器的積分
控制和微分控制與 PID 控制器的參數相同。因此 PI-PD 控制器可以根據 PID 控制參數和 β 值計算得出 Kp、Ti、Kf、Td 參數,通過參數再次整定,能使系統在超調量較小、收斂時間較短的情況下平穩收斂,具有良好的調控效果。
3 仿真分析
通過 Adams 軟件建立四旋翼動力學虛擬樣機,將 Adams 所建模型與 Matlab/Simulink進行聯合仿真,研究控制器對四旋翼姿態控制的調節效果。本文研究的四旋翼參數為:機體質量 m=0.67kg,對稱電機軸距 l=450mm,旋翼轉速與升力關系 8000r/m=9.8N,角度初始值俯仰角 θ=0°、俯仰角期望值 y(r)=0°,仿真步長 t=0.01s。橫滾角 φ 與偏航角 ψ 的仿真結
果類同,本文不再贅述。
(1)使用 PID 控制器調節俯仰角 θ 的角度,整定一組參數 Kp=18、Ki=0.2、Kd=260。而根據 PID 控制器參數,設定不同的 β 值,計算出 PI-PD 控制器的 Kp、Ti、Kf、Td 的參數,仿真結果如圖 3 所示。
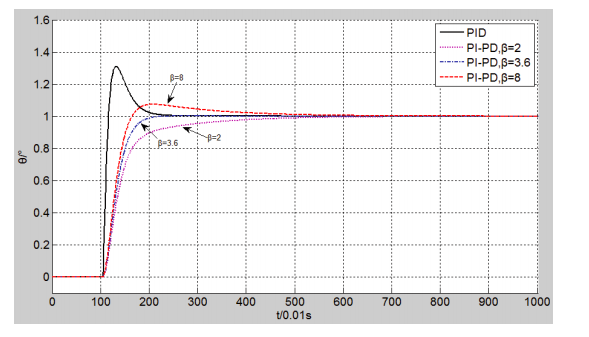
圖 3:PI-PD 控制器不同 β 值仿真結果
在 1s 的時刻,期望值 y(r) 從 0°變為 1°,俯仰角 θ 在 PID 控制器的調節下,收斂時間約為 1.8s,系統超調量約為 30%。
與 PID 控制器的仿真結果比較,當 β 不同時,PI-PD 控制器具有不同的調節效果。而當 β=3.6 時,系統超調量極小,且收斂時間與PID 控制器基本相同。由此可以證明,選取合適的 β 值,PI-PD 控制器可以有效的抑制系統超調量,提高了系統的穩定性。
(2)為 了 使 系 統 收 斂 時 間 更 短, 根據 PI-PD 控制器的調節特性,重新整定參數Kp、Ki、Kd 和 β,仿真結果如圖 4 所示。
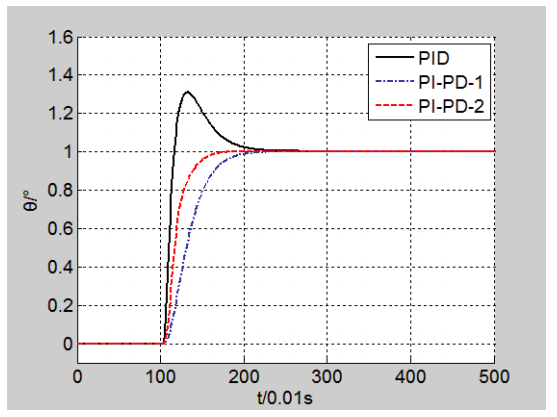
圖 4:PI-PD 控制器不同整定參數仿真結果
仿真結果表明:PID 與 PI-PD-1 的收斂時間約為 1.8s,而 PI-PD-2 的收斂時間約為 0.8s,明顯快于前兩種控制效果。由此證明 PI-PD 控制器對于不同的整定參數,可以在系統無超調量的情況下,縮短系統收斂時間,提高了系統的控制性。
4 結束語
由于四旋翼的非線性和時滯特性,基于PID 控制器的四旋翼姿態控制方式的調節效果較難滿足人們需求。本文基于 PI-PD 控制器,設計了新的四旋翼姿態控制方式。PI-PD 控制器方式可以利用已經整定好的 PID 控制器的參數,根據 β 值計算出控制參數。仿真結果表明
PI-PD 控制器能夠使系統穩定收斂,且很好的抑制了系統超調量,獲得了良好的控制效果。
在今后的工作中,將繼續研究 PI-PD 控制器的參數整定、響應時間、魯棒性等問題,獲得更好的四旋翼姿態控制效果。
-
pcb
+關注
關注
4352文章
23417瀏覽量
406719 -
華強pcb線路板打樣
+關注
關注
5文章
14629瀏覽量
43738
發布評論請先 登錄
小型飛行器專用 AS-DR01模擬信號AI識別跟蹤模塊

原理圖和PCB設計中的常見錯誤
中小尺寸彩屏TFT-LCD顯示控制器RA8889ML3N電路原理圖
請問什么是“循環”PI 控制器?

激光毀傷系統:低空飛行器的 “隱形獵手”
MATLAB在低空飛行器中的應用






 PI-PD 控制器的四旋翼飛行器PCB設計和原理圖
PI-PD 控制器的四旋翼飛行器PCB設計和原理圖











評論