老伙計梯度下降算法在深度學習中扮演著舉足輕重的地位,今天我們來從另一個角度來看這個算法的推演。
我們知道,對于一個足夠光滑的函數,大一時候學過的泰勒展開公式告訴我們,在已知該函數在某一點的各階導數值的情況之下,可以用這些導數值做系數構建一個多項式來近似函數在這一點的鄰域中的值。于是,對于一個損失函數函數g(w),我們現在知道它在w0處的函數值以及各階導數值,如何從w0出發來找到g(w)的極小值呢?我們可以對g(w)在w0點處展開,只保留到一階導數,得到如下公式(其中▽表示梯度):
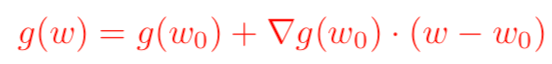
需要注意的是,泰勒公式是一個近似表達式,若w距離w0越近,則近似效果越準確;反過來,若w偏離w0較大,那么近似效果就會比較差。因此,我們在用上式來代表g(w)的時候,應該遵守一個約束條件,這個約束是w距離w0的距離要足夠小。我們可以用距離公式,表示距離的公式有很多,使用最常見的歐幾里得距離公式,并且為了接下來求導方便,加上一個系數1/(2*lr)在前面,于是尋找g(w)的最小值就變成了對下面表達式求關于w的梯度:
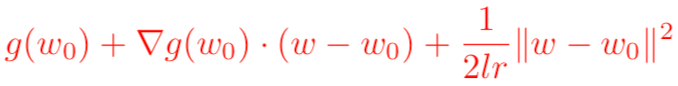
求完梯度之后并設置其等于0,即可得到我們非常熟悉的梯度下降算法的原始公式:
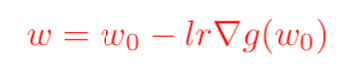
這里的歐幾里得距離公式也可以換成其他距離公式(下文延伸分享其他距離公式)。這同樣也解釋了,我們為什么有時候在損失函數里面加上一個L2損失函數會更好,這樣可以防止梯度更新步幅過大,進而引發損失值發生劇烈的抖動。
延伸:
距離表示的是一個集合中不同元素遠近的度量,當距離為0的時候表示這兩個元素是相同的。數學中,我們學過的距離主要有以下幾種:

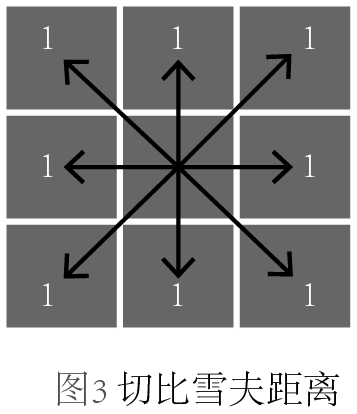
上氏中,當p取不同值得時候,又可以細分為不同的距離,當p=1,稱為曼哈頓距離;當p=2,稱為歐幾里得距離;當p=∞,稱為切比雪夫距離。我們不禁要問,它們的區別是什么?為了更形象地展示它們,我畫了三幅圖來區分,每幅圖中箭頭表示的是從中心點到各個格子中心點的度量:
圖1,曼哈頓距離,它是所有坐標軸差值的求和,可以想象一個城市的街道是完全網格狀的,那么你從一個地方走到另一個地方就必須得走成曼哈頓距離的形狀。
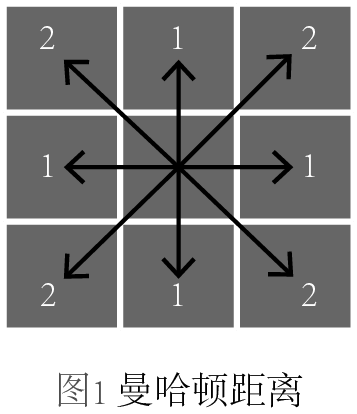
圖2,歐幾里得距離,這種距離是最常見的,勾股定理中用的就是這種距離。

圖3,切比雪夫距離,各個坐標軸差值的最大值。
明可夫斯基距離,又稱明氏距離,是一個定義在賦范空間的距離,賦范空間是指一個由范數構成的向量空間,明氏距離具有平移不變性和同質性,它的公式如下:
除了明氏距離之外,我們在自然語言處理中還用過余弦距離,通常余弦距離是用來判斷兩個元素的相似度(例如文檔或段落),我們可以通過如下公式來得到余弦距離的計算:
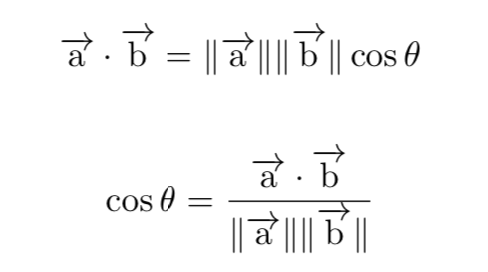
由此可見我們只關心兩個向量的方向是否一致,而并不關心它們各自的幅度。當余弦值為1的時候,代表兩個方向完全一致,即有相似性;當余弦值為0的時候,代表兩個方向正交,可能只有少量相似性;當余弦值為-1的時候,方向完全相反,沒有相似性。
還有一種距離也蠻常見,叫做馬氏距離,它是衡量一個點到一個分布之間的距離,或者說偏離程度。給定分布的均值μ和協方差S,從點x到該分布的馬氏距離的計算公式如下:

以上就是我們常見的距離及其表達式。
-
算法
+關注
關注
23文章
4698瀏覽量
94742 -
梯度
+關注
關注
0文章
30瀏覽量
10460 -
深度學習
+關注
關注
73文章
5554瀏覽量
122482
原文標題:從泰勒展開來看梯度下降算法
文章出處:【微信號:DeepLearningDigest,微信公眾號:深度學習每日摘要】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄





 梯度下降算法在深度學習中扮演著舉足輕重的地位
梯度下降算法在深度學習中扮演著舉足輕重的地位











評論