1 原理

1.1 引入

線性回歸是最為常用的一種數據分析手段，通常我們拿到一組數據后，都會先看一看數據中各特征之間是否存在明顯的線性關系。例如，現在我們拿到了一組學校中所有學生基本資料的數據，該數據以二維表格的形式呈現，如下表所示。

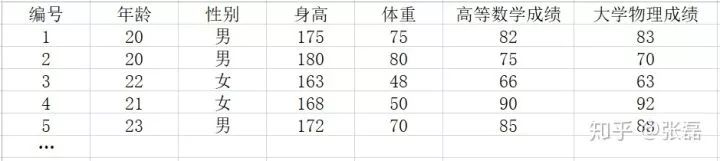
示例數據表

每行代表一個學生，每列代表該學生的一個屬性（或稱為特征），那么如果我們對特征進行仔細觀察，不難發現身高和年齡總是呈現正相關關系，數學成績與物理成績也基本呈現正相關關系。那么我們是否可以給這樣的兩個特征之間擬合出一條近似的直線來表達他們之間的線性函數關系呢？這里我們的想法其實就是機器學習的世界觀：數據驅動構建模型。

1.2 模型

只不過這里的模型非常簡單，只是線性模型，也就是一條直線方程，通長我們可以表達成如下公式：

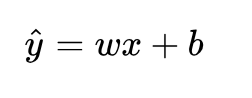
這里，數據中我們將某一特征列作為自變量 x （例如身高），因變量 y （如體重）也就是我們想要預測的值， x 和 y 都已知，現在的任務就是：加入新增了一個 x ，而其對應的 y 未知，那么我們該如何預測出一個 它？顯然，我們需要構建 y 與 x 之間的函數關系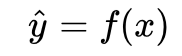：對于身高體重這樣的簡單問題而言，就可以直接使用上述的線性方程作為我們想要擬合的模型。

接下來的問題就是，如何擬合這個模型，也就是說，如何求得線性模型中的兩個參數 w 和 b？

1.3 損失函數

要求解最佳的參數，首先我們需要讓計算機知道一個目標，畢竟解決任何問題都需要確立一個明確的目標才行，對于計算機這樣的數字世界，我們就需要給它確定一個定量化的目標函數式，在優化問題中，我們通常稱之為目標函數，或者損失函數（Loss function）。無論我們選擇什么樣的模型，最終都是可以得到一組預測值 ，對比已有的真實值 y ，數據行數為 n ，我們很自然地可以將損失函數定義如下：

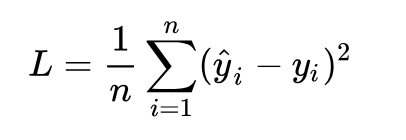
即預測值與真實值之間的平均的平方距離，統計中我們一般稱其為MAE（mean square error）均方誤差。把之前我們確定的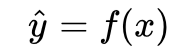 帶入損失函數：

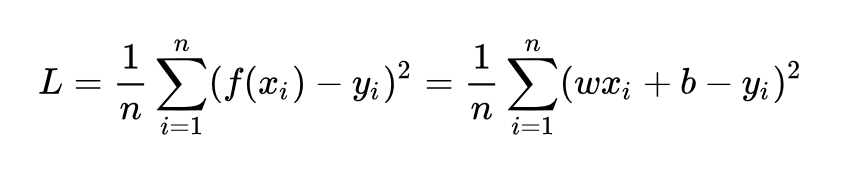
注意，對于損失函數 L 而言，其自變量不再是我們習慣中的 x（其實 x 和 y 都是在訓練數據中的已知值），損失函數 L 的自變量應該是我們要求解的參數 w 和 b，因此我們可以把損失函數重新記為：

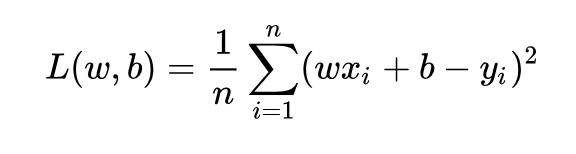
現在，我們的任務就是希望把這個損失函數交給計算機，然后跟計算機說，幫我把這個函數最小化，然后告訴我 L 最小時的一組 w 和 b 是多少就行了。但是顯然計算機還沒那么聰明，它并不知道怎么算，我們還是要靠自己解決。

核心的優化目標式：

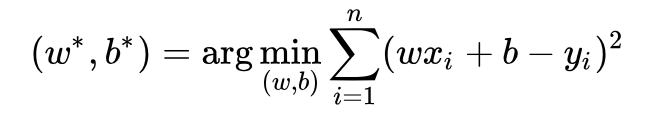
這里有兩種方式：

一種是“最小二乘法”（least square method），可直接求解；

另一種是梯度下降（gradient descent），有關梯度下降的方法原理可參考我之前這篇文章 -》 ［link］。

1.4 最小二乘法

求解 和 是使損失函數最小化的過程，在統計中，稱為線性回歸模型的最小二乘“參數估計”（parameter estimation）。我們可以將 L 分別對 w 和 b 求導，得到：

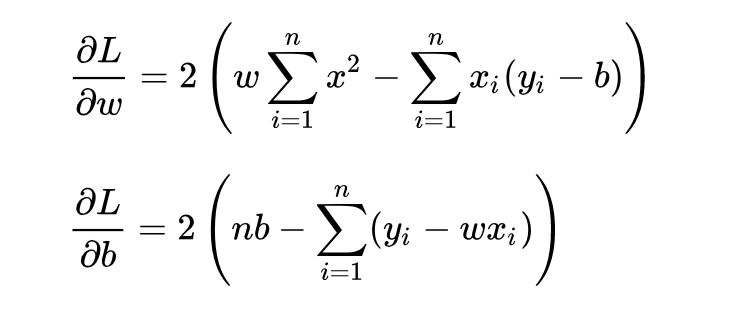
令上述兩式為0，可得到 w 和 b 最優解的閉式（closed-form）解：

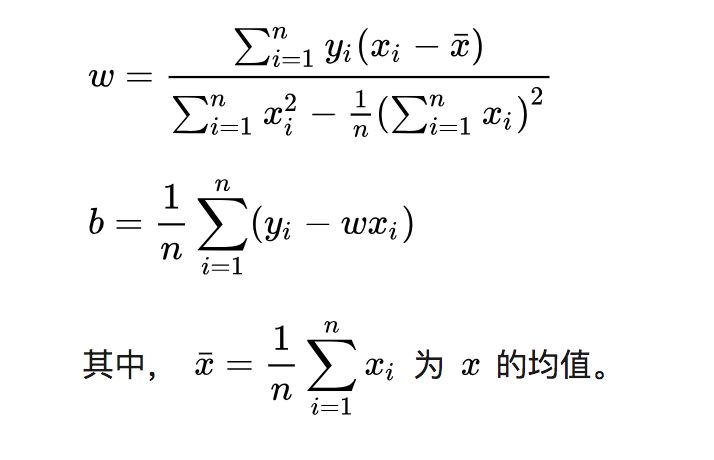
1.5 梯度下降法求解

2 代碼實現 （使用梯度下降法）

首先建立 liner_regression.py 文件，用于實現線性回歸的類文件，包含了線性回歸內部的核心函數。

建立 train.py 文件，用于生成模擬數據，并調用 liner_regression.py 中的類，完成線性回歸任務。

顯示結果：

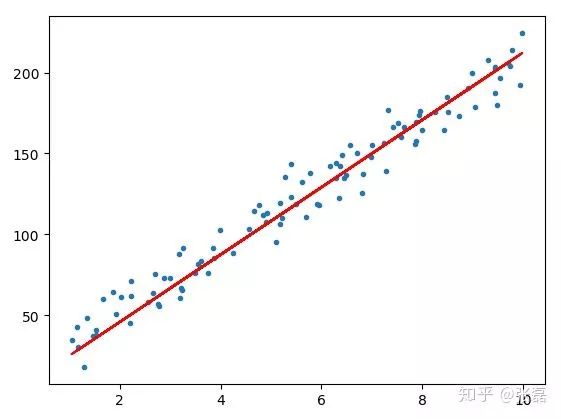
原始數據x， y和擬合的直線方程

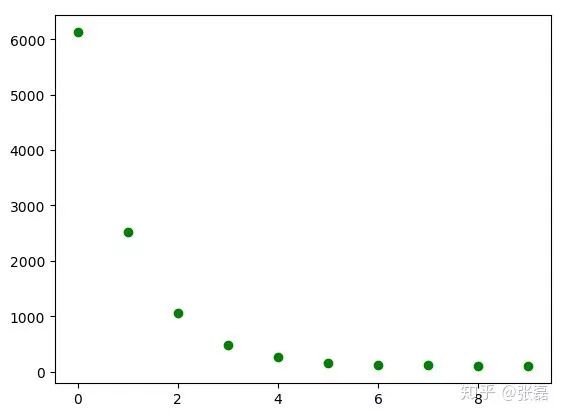
利用梯度下降法優化過程中損失函數的下降情況