編者按：反向傳播是一種訓練人工神經網絡的常見方法，它能簡化深度模型在計算上的處理方式，是初學者必須熟練掌握的一種關鍵算法。對于現代神經網絡，通過反向傳播，我們能配合梯度下降大幅提高模型的訓練速度，在一周時間內就完成以往研究人員可能要耗費兩萬年才能完成的模型。

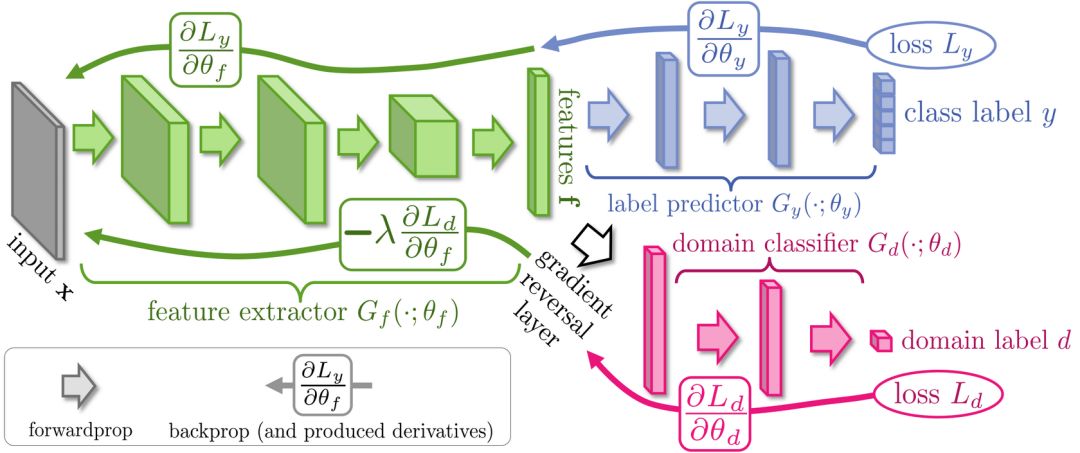
除了深度學習，反向傳播算法在許多其他領域也是一個強大的計算工具，從天氣預報到分析數值穩定性——區別只在于名稱差異。事實上，這種算法在幾十個不同的領域都有成熟應用，無數研究人員都為這種“反向模式求導”的形式著迷。

從根本上說，無論是深度學習還是其他數值計算環境，這是一種方便快速計算的方法，也是一個必不可少的計算竅門。

計算圖

談及計算，有人可能又要為煩人的計算公式頭疼了，所以本文用了一種思考數學表達式的輕松方法——計算圖。以非常簡單的e=(a+b)×(b+1)為例，從計算角度看它一共有3步操作：兩次求和和一次乘積。為了讓大家對計算圖有更清晰的理解，這里我們把它分開計算，并繪制圖像。

我們可以把這個等式分成3個函數：

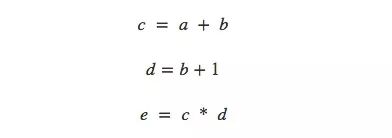
在計算圖中，我們把每個函數連同輸入變量一起放進節點中。如果當前節點是另一個節點的輸入，用帶剪頭的線表示數據流向：

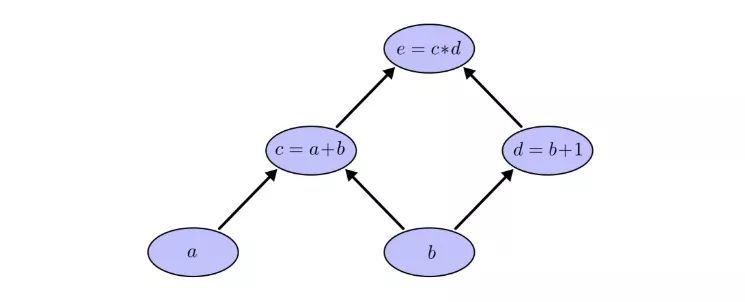
這其實是計算機科學中的一種常見描述方法，尤其是在討論涉及函數的程序時，它非常有用。此外，現在流行的大多數深度學習開源框架，比如TensorFlow、Caffe、CNTK、Theano等，都采用了計算圖。

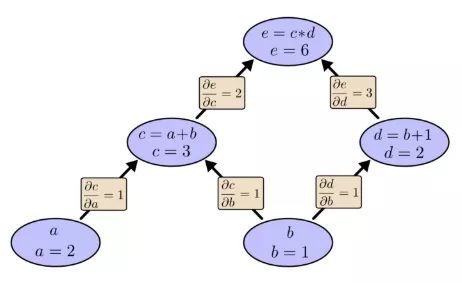
仍以之前的例子為例，在計算圖中，我們可以通過設置輸入變量為特定值來計算表達式。如，我們設a=2，b=1：

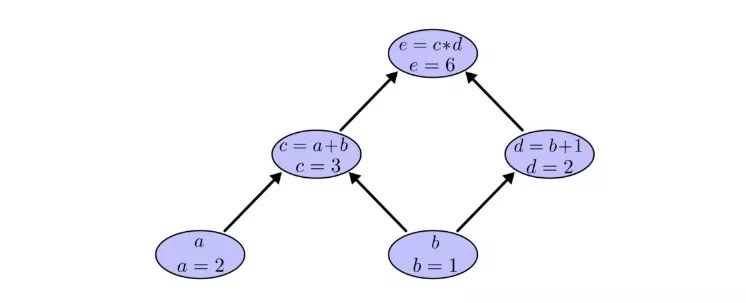
可以得到e=(a+b)×(b+1)=6。

計算圖上的導數

如果要理解計算圖上的導數，一個關鍵在于我們如何理解每一條帶箭頭的線（下稱“邊”）上的導數。以之前的連接a節點和c=a+b節點的邊為例，如果a對c有影響，那這是個怎么樣的影響？如果a變化了，c會怎么變化？我們稱這為c關于a的偏導數。

為了計算圖中的偏導數，我們先來復習這兩個求和規則和乘積規則：

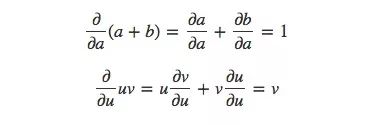
已知a=2，b=1，那么相應的計算圖就是：

現在我們計算出了相鄰兩個節點的偏導數，如果我想知道不直接相連的節點是如何相互影響的，你會怎么辦？如果我們以速率為1的速度變化輸入a，那么根據偏導數可知，函數c的變化速率也是1，已知e相對于c的偏導數是2，那么同樣的，e相對a的變化速率也是2。

計算不直接相連節點之間偏導數的一般規則是計算各路徑偏導數的和，而同一路徑偏導數則是各邊偏導數的乘積，例如，e關于b的偏導數就等于：

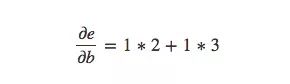
上式表示了b是如何通過影響函數c和d來影響函數e的。

像這種一般的“路徑求和”規則只是對多元鏈式規則的不同思考方式。

路徑分解

“路徑求和”的問題在于，如果我們只是簡單粗暴地計算每條可能路徑的偏導數，我們很可能會最后得到一個“爆炸”的和。

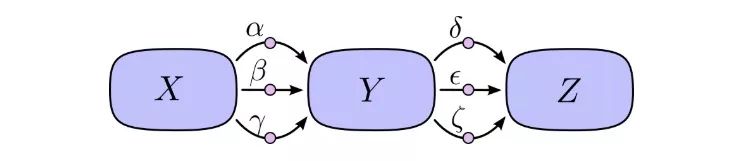
如上圖所示，X到Y有3條路徑，Y到Z也有3條路徑，如果要計算?Z/?X，我們要計算的是3×3=9條路徑的偏導數的和：

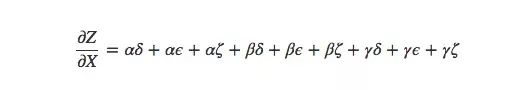
這還只是9條，隨著模型變得越來越復雜，相應的計算復雜度也會呈指數級上升。因此比起傻乎乎地一個個求和，我們最好能記起一些小學數學知識，然后把上式轉為：

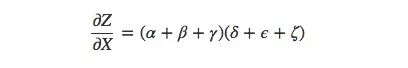
是不是很眼熟？這就是前向傳播算法和反向傳播算法中最基礎的一個偏導數等式。通過分解路徑，這個式子能更高效地計算總和，雖然長得和求和等式有一定差異，但對于每條邊它確實只計算了一次。

前向模式求導從計算圖的輸入開始，到最后結束。在每個節點上，它匯總了所有輸入的路徑，每條路徑代表輸入影響該節點的一種方式。相加后，我們就能得到輸入對最終結果的總的影響，也就是偏導數。

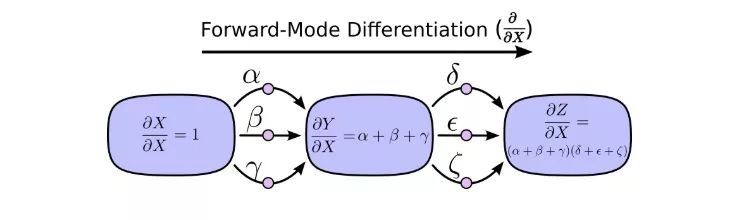
雖然你以前可能沒想過從計算圖的角度來進行理解，但這樣一看，其實前向模式求導和我們剛開始學微積分時接觸的內容差不多。

另一方面，反向模式求導則是從計算圖的最后開始，到輸入結束。對于每個節點，它做的是合并所有源自該節點的路徑。

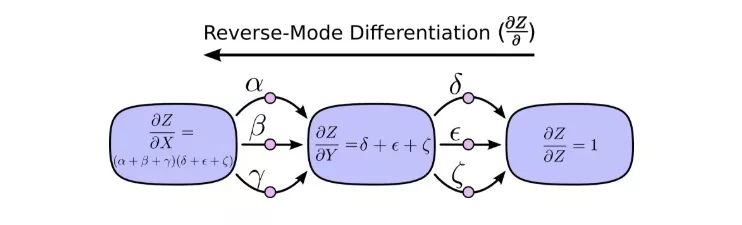
前向模式求導關注的是一個輸入如何影響每個節點，反向模式求導關注的是每個節點如何影響最后那一個輸出。換句話說，就是前向模式求導是在把?/?X塞進每個節點，反向模式求導是在把?Z/?塞進每個節點。

大功告成

說到現在，你可能會想知道反向模式求導究竟有什么意義。它看起來就是前向模式求導的一個奇怪翻版，其中會有什么優勢嗎？

讓我們從之前的那張計算圖開始：

我們先用前向模式求導計算輸入b對各個節點的影響：

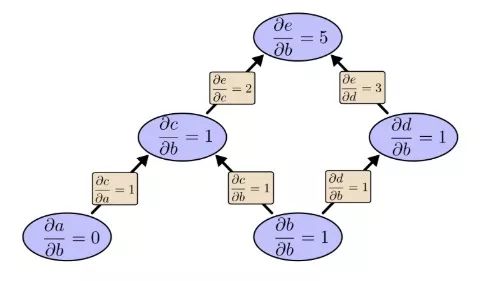
?e/?b=5。我們把這個放一邊，再來看看反向模式求導的情況：

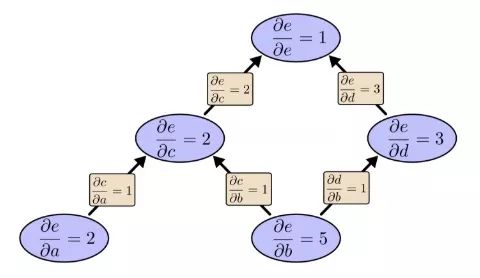
之前我們說反向模式求導關注的是每個節點如何影響最后那個輸出，根據上圖可以發現，圖中偏導數既有?e/?b的，也有?e/?a的。這是因為這個模型有兩個輸入，而它們都對輸出e產生了影響。也就是說，反向模式求導更能反映全局輸入情況。

如果說這是一個只有兩個輸入的簡單例子，兩種方法都無所謂，那么請想象一個有一百萬個輸入、只有一個輸出的模型。像這樣的模型，我們用前向模式求導要算一百萬次，用反向模式求導只要算1次，這就高下立判了！

在訓練神經網絡時，我們把cost（描述網絡表現好壞的值）視作一個包含各類參數（描述網絡行為方式的數字）的函數。為了提升模型性能，我們要不斷改變參數對cost函數求導，以此進行梯度下降。模型的參數千千萬，但它的輸出只有一個，因此機器學習對于反向模式求導，也就是反向傳播算法來說是個再適合不過的應用領域。

那有沒有一種情況下，前向模式求導能比反向模式求導更好？有的！我們到現在談的都是多輸入單輸出的情形，這時反向更好；如果是一輸入多輸出、多輸入多輸出，前向模式求導速度更快！

這不是太普通了嗎？

當我第一次真正理解反向傳播算法時，我的反應是：哦，就是最簡單的鏈式法則！我怎么花了這么久才明白？事實上我也不是唯一出現這種反應的人，的確，如果問題是你能從前向模式求導中推出那種更聰明的計算方法，這就沒那么麻煩了。

但我認為這比看起來要困難得多。在反向傳播算法剛發明的時候，人們其實并沒有十分關注前饋神經網絡的研究。所以也沒人發現它的衍生品有利于快速計算。但當大家都知道這種衍生品的好處后，他們又開始反應過來：原來它們有這樣的關系！這之中有一個惡性循環。

更糟糕的是，在腦子里推一推算法的衍生工具是很普遍的，一旦涉及用它們訓練神經網絡，這幾乎就等同于洪水猛獸。你肯定會陷入局部最小值！你可能會浪費巨大的計算成本！人們只有在確認這種方法有效后，才會乖乖閉嘴去實踐。

小結

衍生工具比你想象中的更易于挖掘，也更好用，我希望這是本文為你帶來的主要經驗。雖然事實上這個挖掘過程并不容易，但在深度學習中領會這一點很重要，換一個角度，我們就能發現不同的風景。同樣的話也適用于其他領域。

還有其他經驗嗎？我認為有。

反向傳播算法也是了解數據流經模型過程的有利“鏡頭”，我們能用它知道為什么有些模型會難以優化，如經典的遞歸神經網絡中梯度消失的問題。

最后，讀者可以嘗試同時結合前向傳播和反向傳播兩種算法來進行更有效的計算。如果你真的理解了這兩種算法的技巧，你會發現其中會有不少有趣的衍生表達式。