?
前一章詳解了TX7006上的線性計算,AD/DA動態分析中的傅里葉變換和動態參數計算。
【前文回顧】技術干貨 | ATX7006線性計算與AD/DA動態分析解析-電子發燒友網
本章將繼續介紹AD/DA動態分析中的信號窗口:
1、簡介
傅里葉變換假定(采樣)信號是無限的。因此,最后一個采樣點的幅度應恰好在第一個采樣點(的幅度)前一個采樣點結束。采集到的正弦波數量應為整數。換句話說,如果將采集到的信號依次重復排列,信號應是連續的。具有整數個采樣點的采集信號是相干的。
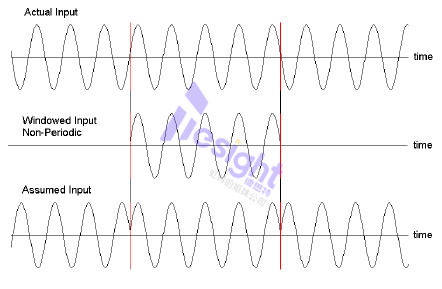
并不總是能夠捕捉到整數的正弦波(也就是2的冪次)。對于傅立葉變換來說,這意味著信號是不連續的(信號的終點和起點不平滑)。在頻譜中,這將導致頻譜泄漏。見下圖:按下“顯示頻譜”按鈕,在相干和非相干之間切換。

2、不連貫信號的窗口處理
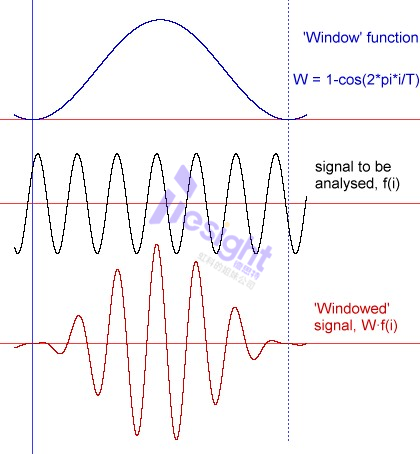
對不連貫的捕獲信號進行傅立葉分析,將無法計算出可用的參數(SINAD、信噪比等),而且諧波可能會在頻譜中被忽略。為了減少不連續性的影響,我們可以在信號開始和結束時減小捕獲信號的振幅。這正是信號窗口的作用。在上圖中顯示信號并選擇一個窗口。在頻譜中,它會在感興趣的頻點周圍產生額外的頻點。信號窗口的計算公式位于繪圖下方。該信號與捕捉到的信號相乘。
幅度誤差
在上圖中選擇相干、矩形窗口,以電壓峰值顯示頻譜。振幅正好與1Vpeak吻合。現在選擇非相干,注意振幅誤差。載波的能量分散到了其他頻帶。選擇dBc(相對于載波的dBs)時,可以更好地看到這一點。切換回Vpeak,選擇相干信號、掃描窗口。載波振幅為0.5V。其他能量被置于載波兩側的2個分區中。總振幅為1Vpeak(0.5V+2*0.25V)。然后選擇非相干信號。仍然會有振幅誤差,但會小于矩形窗口。
參數計算
正如我們在前面的示例中看到的,信號窗口可以減少頻譜泄漏,并將信號能量置于信號周圍的額外分段中。參數計算將更加合理,諧波也能在頻譜中重新識別。RifeVincent4窗口會將感興趣信號的幾乎所有能量都置于信號周圍的額外頻帶中。然而,這其中存在一個問題。為了說明這一點,請參閱下一個實驗。
窗口頻率分辨率問題
顯示頻譜(按下“顯示信號”按鈕),選擇dBc、0.5V直流、相干信號并選擇Hamming窗。信號能量分布在3個bin中,即5號bin及5號bin兩側各1個額外bin。直流能量分布在第1和第2個bin中,信號與直流bin之間的bin(2號和3號bin)為噪聲bin。
選擇RifeVincent4窗。信號能量分布在9個bin中(去除直流后計數),中心位于5號bin位置,5號bin兩側各有4個bin。直流分量的情況同理。由于信號與直流bin之間僅有3個bin,因此1號至4號bin中同時包含直流和信號成分。
諧波bin與噪聲bin之間也可能發生同樣的情況。如果某諧波bin的幅度低于或等于其周圍噪聲bin的幅度,該諧波會“吸收”(泄漏)噪聲bin的能量。因此,當啟用窗函數且諧波幅度等于或低于噪聲時,總諧波失真(THD)可能顯著惡化。
3、選擇窗函數
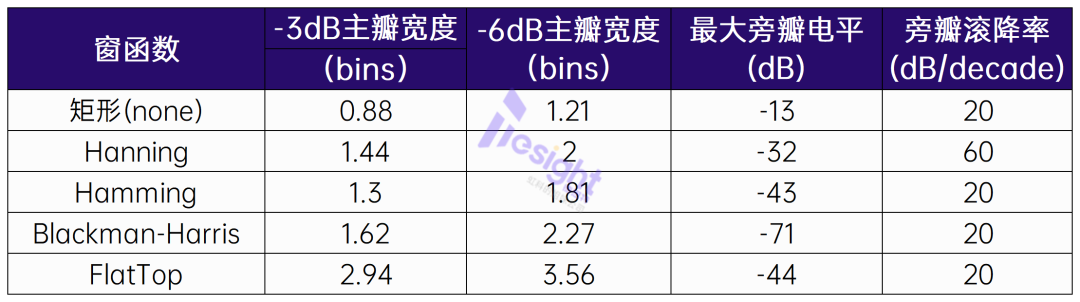
窗函數之間的一個重要區別在于主瓣寬度和旁瓣特性。主瓣由中心頻率及其兩側的一個或多個頻率bins(頻段)組成。當選擇相干信號(無直流)時,這一點可在上述繪圖中觀察到。更改窗函數將改變中心頻率周圍的bins數量。旁瓣是不屬于主瓣的bins。主瓣寬度決定了頻率分辨率(即我們區分信號的能力)——主瓣越寬,頻率分辨率越差,但幅度精度越好。如果幅度精度是關鍵問題,FlatTop 或 Blackman-Harris 窗可能是不錯的選擇,但其主瓣較寬,導致頻率分辨率較差。
Hamming 窗和 Hanning 窗的形狀相似(也可參見兩者的數學表達式)。它們的幅度精度較差,但頻率分辨率優于 FlatTop 和 Blackman-Harris 窗。兩者的主要區別在于旁瓣的滾降速率。
RifeVincent4 窗的旁瓣電平極低,但主瓣較寬。對于單音信號下的A/D和D/A轉換器動態測試,這可能是一個合適的選擇。但需注意,由于主瓣較寬,諧波的主瓣也會較寬,導致相鄰噪聲bins的能量泄漏到諧波bins中,這通常會導致總諧波失真(THD)較差(相對而言)。
窗函數特性
下表列出了各種窗函數的一些特性。最大旁瓣電平是指相對于主瓣而言,最大旁瓣的電平值(以分貝為單位)。旁瓣滾降速率是指旁瓣峰值隨頻率每十倍頻程衰減的速率(以分貝/十倍頻程為單位)。
?
-
芯片測試
+關注
關注
6文章
150瀏覽量
20724 -
動態分析
+關注
關注
1文章
20瀏覽量
7385
發布評論請先 登錄
2014 中國信號處理技術工程師年會
基于部分動態可重構技術的信號解調系統該怎么設計?
基于數據窗口對象SQL 語法的動態移植技術探討
數字信號處理技術的優點分析
技術干貨 | ATX7006線性計算與AD/DA動態分析解析






 技術干貨 | AD/DA動態分析中的信號窗口處理技術
技術干貨 | AD/DA動態分析中的信號窗口處理技術

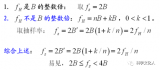










評論