今天來學習波特圖，對于很多閉環系統，我們需要畫出其波特圖去分析其穩定性，而且一個系統動靜態性能的好壞可以從波特圖中直觀的體現出來。在講解波特圖之前，我們先來回顧一下復數知識，下圖為復平面，即以實部為x軸和虛部為y軸的坐標系。給定一個復數，我們可以通過以下兩個公式求出其模和幅角，而且分貝概念的定義就是20倍的增益的模取以10為底的對數。這里選擇對數的原因為可以在有限的坐標下包含更大的頻率范圍。

接下來，再來看一下一階系統的波特圖，首先給出一階系統的傳遞函數，并且取其模，這里對分數取模等于對分子分母分別取模再相除，再取對數得到增益的分貝形式，這里直流增益為0dB，還可以得到其角度，右下圖為二階系統的波特圖，但是我們可以只看其低頻部分（<100kHz），在頻率非常底的時候（<1Hz），系統增益為直流增益，而對于RC一階濾波系統來說，直流增益為0dB，頻率在大于第一個極點時，增益以每十倍頻程-20dB下降，幅角為-45度，在之后將降低到-90度。

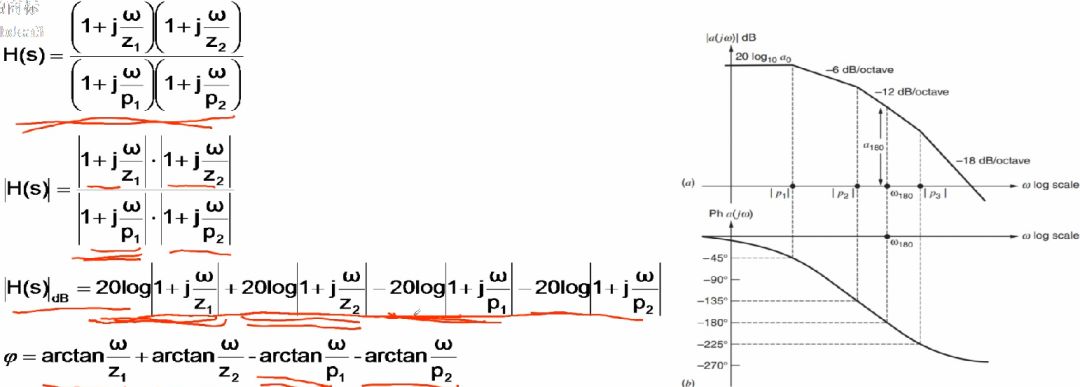
接下來，再來講解二階系統的波特圖，同樣的，我們先來回顧一下數學知識，利用歐拉公式能夠簡化復數的乘法和除法運算，通過下式觀察可知，復數相乘，結果的模為兩個乘數的模的乘積，結果的幅角為兩個乘數幅角的和。同理，復數相除，其模相除，其幅角相減。

這樣我們在計算二階系統的模和幅角就會方便的多，首先將傳遞函數分子分母因式分解得到下式，再對其取模，這里可以先用除法關系，這樣模為分子分母模的商，再利用乘法關系，這樣模為各個因式的模，幅角同理，為分子各因式幅角的和再減去分母各因式的幅角。這樣就可以畫出其波特圖，再來看右邊的波特圖，在第一個極點之后，增益以-20dB每十倍頻下降（圖中為-6dB每倍頻下降，但下降速率是相同的），相角下降到-45度，之后在無窮遠處下降到-90度，在第二個極點之后，增益以-40dB每十倍頻下降，相角下降到-135度，之后在無窮遠處下降到-180度。總結一下，極點的作用就是，在增益上面，改變極點頻率之后的斜率，每經過一個極點之后增益下降速率增加-20dB每十倍頻程，而在相角方面，對相角的改變是逐漸產生的，具體體現在每經過一個極點之后角度由前一個角度逐漸減小45度，并在之后再逐漸減小45度。零點與之類似，其作用就是，在增益上面，改變零點頻率之后的斜率，每經過一個零點之后增益上升速率增加20dB每十倍頻程，而在相角方面，對相角的改變是逐漸產生的，具體體現在每經過一個極點之后角度由前一個角度逐增加45度，并在之后再逐漸增加45度。可以看出，零極點的作用相反，所以采用增加零點或極點的方式抵消掉極點或零點來對系統進行校正。

當電阻和電容并聯時會產生一個極點。

當電阻和電容串聯時會產生一個零點和零極點。

下面再對下面電路的波特圖進行分析，也是運放電路常用的一種形式，先從阻抗的角度進行分析，得到會產生一個低頻極點和高頻零點。這里零點和極點的定義是讓每個因式為零的S的解，再從反饋的角度進行分析，產生的是一個高頻極點和低頻零點。