數(shù)學一直是我認為非常神奇的學科。上學期間不知數(shù)學有何用，甚至覺得數(shù)學專業(yè)連工作都找不到，當然那時還沒有什么AI的概念。

自從接觸機器學習、深度學習以后，才知道自己原來的認知簡直太渺小了，數(shù)學豈止是強大，它一直在改變世界。

下面是17個可以改變世界的公式，有的學過，有的沒學過，一起和大家復習一下。個人喜歡的是第6個歐拉公式。

1 勾股定

英文：

Pythagoras’ Theorem

公式：

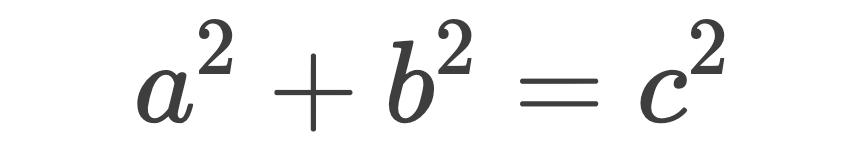
定義：

在平面上的一個直角三角形中，兩個直角邊邊長的平方加起來等于斜邊長的平方。

這個基本幾何定理，在公元前11世紀，數(shù)學家商高（西周初年人）就提出“勾三、股四、弦五”。

而在西方，希臘數(shù)學家畢達哥拉斯在公元前6世紀證明了勾股定理，因而西方人都習慣地稱這個定理為畢達哥拉斯定理（Pythagoras’ Theorem）。

“老畢”還證明過黃金分割線，他創(chuàng)辦的畢達哥斯拉學派是古希臘四大門派之一。

勾股定理被認為是論證幾何的發(fā)端，它是歷史上第一個把數(shù)與形聯(lián)系起來的定理，也是歷史上第一個給出了完全解答的不定方程。

這條定理不僅在幾何學中是一顆光彩奪目的明珠，更是被譽為“幾何學的基石”。

2 對數(shù)

英文：

Logarithms

公式：

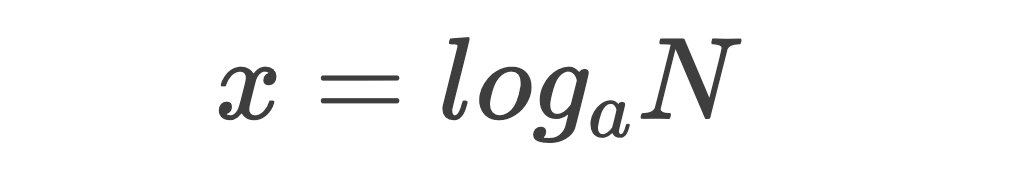
定義：

如果a的x次方等于N（a》0，且a≠1），那么數(shù)x叫做以a為底N的對數(shù)。

對數(shù)方法是由數(shù)學家約翰·皮納爾在1614年發(fā)明。

但這個方法無論是放在當時還是現(xiàn)在，都具有重要意義，它的出現(xiàn)讓許多繁難的計算成為了可能。

也正因如此，在計算器和計算機出現(xiàn)之前，它持久地被用于測量、航海以及其他實用數(shù)學分支中。

3 微積分

英文：

Calculus

公式：

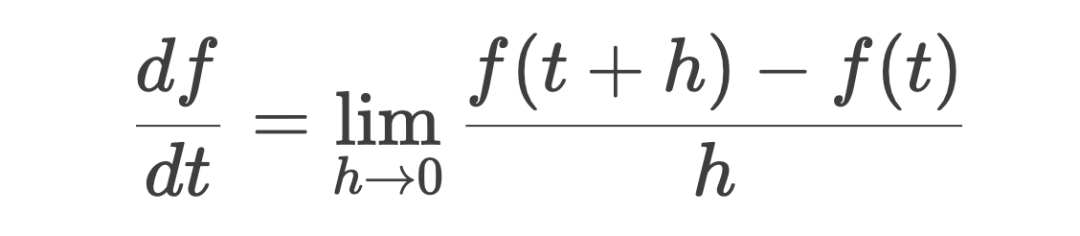
此處給出的公式，是微積分中導數(shù)的定義。

其實微積分是高等數(shù)學中研究函數(shù)的微分（Differentiation）、積分（Integration）以及有關概念和應用的數(shù)學分支。

微分學包括求導數(shù)的運算，是一套關于變化率的理論。它使得函數(shù)、速度、加速度和曲線的斜率等均可用一套通用的符號進行討論。

而積分學，包括求積分的運算，為定義和計算面積、體積等提供一套通用的方法。

馮·諾依曼曾經(jīng)這樣評價微積分：

它是現(xiàn)代數(shù)學的第一個成就，而且怎樣評價它的重要性都不為過。

我認為，微積分比其他任何事物都更清楚地表明了現(xiàn)代數(shù)學的發(fā)端；而且，作為其邏輯發(fā)展的數(shù)學分析體系仍然構成了精密思維中最偉大的技術進展。

許多初等數(shù)學無法解決的問題，微積分往往都可以迎刃而解，而且許多自然現(xiàn)象也可以通過建立微分方程來描述。

也正因如此，微積分廣泛地被應用于運動學、天文學、經(jīng)濟學、社會學、化學、生物學等。

4 萬有引力定律

英文：

Law of Gravity

公式：

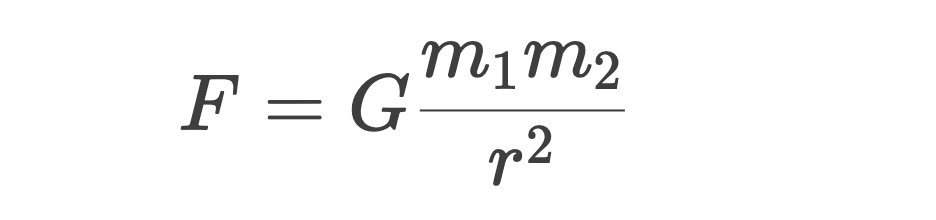
定義：

任何兩個質點都存在通過其連心線方向上的相互吸引的力：

該引力大小與它們質量的乘積成正比與它們距離的平方成反比，與兩物體的化學組成和其間介質種類無關。

其中，F(xiàn)表示兩個物體之間的引力；G表示萬有引力常量；m1和m2分別表示物體1和物體2的質量；r則是兩個物體之間的距離（大小）。

萬有引力定律是牛頓于1687年在《自然哲學的數(shù)學原理》上所發(fā)表，可以說是17世紀自然科學最偉大的成果之一。

他用萬有引力定律證明了開普勒定律、月球繞地球的運動、潮汐的成因和地球兩極較扁等自然現(xiàn)象。

因此，牛頓的萬有引力定律是天體力學的基礎。人造衛(wèi)星、月球和行星探測器的軌道，都是以這個定律為基礎來計算的。

5 -1的平方根

英文：

The square root of -1

公式：

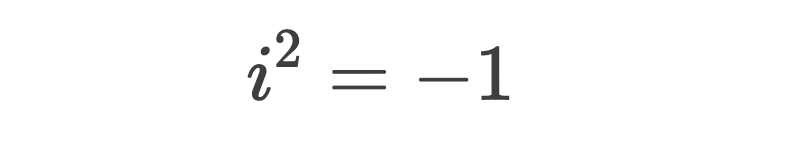
數(shù)學家們一直在對數(shù)字的概念做著拓展工作，例如從自然數(shù)到負數(shù)、分數(shù)，再到實數(shù)。

而在16世紀，意大利米蘭學者卡當首次引入了復數(shù)的概念。

經(jīng)過達朗貝爾、棣莫弗、歐拉、高斯等人的工作，這個概念逐漸被數(shù)學家接受。

從數(shù)學角度來看，復數(shù)可以說是極其優(yōu)雅，任何方程都有一個復數(shù)解，但這種情況在實數(shù)卻不成立。

例如，對于x2 + 4 = 0，就是沒有實數(shù)解的，而放眼復數(shù)，解就是-4或2i。

而微積分也是可以拓展到復數(shù)，數(shù)學家們由此還發(fā)現(xiàn)了一些數(shù)所具備的對稱性和性質。

這些特性便使得復數(shù)在電子學和信號處理中起到了重要的作用。

6 多面體歐拉定理

英文：

Euler’s Polyhedra Formula

公式：

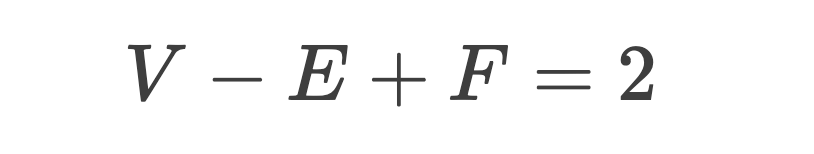
定義：

對于n維空間中的簡單多面體，其零維對象數(shù)（即頂點數(shù)）D0、一維對象數(shù)（即邊數(shù)）D1、二維對象數(shù)（即面數(shù)）D2、三維對象數(shù)（即體數(shù)）D3、……、n維對象數(shù)Dn：

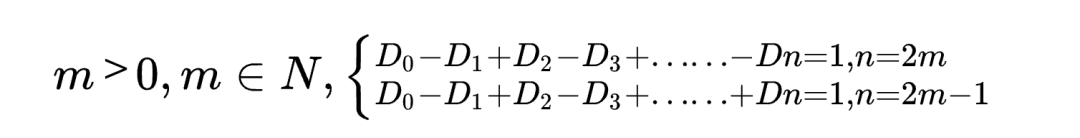
其中符號為正負號交替出現(xiàn)，等式一邊是各維對象數(shù)的重復加減，等式另一邊是1。

一般以V（Vertex）表示零維對象（即頂點）數(shù)D0，以E（Edge）表示一維對象（即邊、棱）數(shù)D1，以F（Flat surface）表示二維對象（即面）數(shù)D2，以S（Solid）表示三維對象（即體）數(shù)D3，以P表示四維對象數(shù)D4。

對于一般的三維空間，該公式表達為：V - E + F - S= 1。

由于對于一個三維物體，其體數(shù)S總是1，因此就得到上述的那個公式。

歐拉的這項觀察，現(xiàn)在被視為拓撲不變性的最早的例子之一。

連同他對柯尼斯堡橋問題的解決，可以說是為拓撲學的發(fā)展鋪平了道路，使其成為現(xiàn)代物理學必不可少的一個數(shù)學分支。

這也是馬斯克喜歡的公式，翻譯過來就是：eiπ + 1 = 0，即被稱為史上最美公式的歐拉公式。

由于篇幅原因，其它公式便不一一展開，感興趣的友友們可以點文末鏈接查看詳情。