我們知道,濾波器通常用于降低噪聲并提高數(shù)據(jù)質(zhì)量。
注意這個(gè)濾,指的是衰減而非一刀切~
但是在濾波的過程中會出現(xiàn)各種問題,這些問題有的會對最終結(jié)果產(chǎn)生極大的影響,導(dǎo)致我們的結(jié)果很難解釋清楚。
腦科學(xué)的主要挑戰(zhàn)之一是在測量時(shí)會存在噪聲和偽跡污染。
這些可能包括環(huán)境噪聲,儀器噪聲或由體內(nèi)信號源產(chǎn)生的噪聲,很明顯,我們對這些干擾信號不感興趣。
舉個(gè)最簡單的例子,如果信號和干擾占據(jù)不同的頻段,那么我們可以通過對數(shù)據(jù)應(yīng)用濾波器來改善信噪比(SNR),也就是將干擾衰減至最低,同時(shí)保證有用信號完美通過。
而濾波,也就是對信號進(jìn)行不同程度地衰減,也可以理解為對信號的放大倍率進(jìn)行處理,一個(gè)意思。
接下來,我們來看一看從數(shù)據(jù)記錄到最終展示出來,都在哪里應(yīng)用到了濾波:
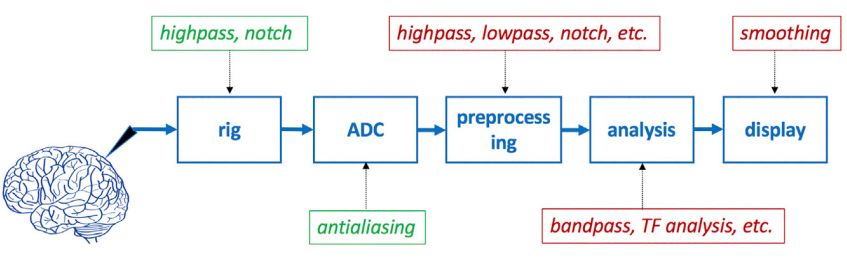
共5處,綠色框處為模擬濾波,紅色框處為數(shù)字濾波。
我們最開始采集到的大腦數(shù)據(jù)是連續(xù)的模擬信號,為了轉(zhuǎn)換成我們處理起來更方便的離散的數(shù)字信號,就會用到 ADC (模擬-數(shù)字轉(zhuǎn)換器)。對于現(xiàn)代信號處理來說,這種處理已經(jīng)從模擬領(lǐng)域逐漸轉(zhuǎn)至數(shù)字領(lǐng)域了。
① 測量裝置或放大器
可能包括 高通濾波器和陷波濾波器 ,而像腦電這類記錄細(xì)胞外腦活動(dòng)的測量裝置的放大器通常是交流耦合的,所以這里可以省略高通。
PS:這里可能會涉及一些耦合電容等電路上的概念,就不展開講了,有興趣的讀者可自行百度~
② ADC
就是模數(shù)轉(zhuǎn)換,但在 AD轉(zhuǎn)換 (模-數(shù)轉(zhuǎn)換)之前,會有一個(gè)低通抗混疊濾波器。這個(gè)抗混疊濾波器的作用是:濾除奈奎斯特頻率以上的頻率分量。
這里單獨(dú)講一講:當(dāng)今的數(shù)據(jù)處理幾乎都是在數(shù)字領(lǐng)域進(jìn)行的,這就要求信號在時(shí)間上進(jìn)行離散采樣。而在采樣過程中只保留采樣點(diǎn)的值,因此此時(shí)的信號是模糊的。
如果這種采樣信號滿足一定的條件,那么就可以完美重建原始信號,這里引入 奈奎斯特采樣定理 :采樣頻率要大于兩倍信號所包含的最高頻率;
但在真正應(yīng)用時(shí),我們一般都會取最高頻的3~5倍或更高,來作為采樣頻率。這個(gè)采樣頻率的一半,就稱作奈奎斯特頻率,或奈奎斯特極限,這個(gè)極限是完美重構(gòu)原始信號的關(guān)鍵。
而如果在采樣時(shí),奈奎斯特頻率以上還存在更高的頻率分量,那么我們還原后的數(shù)字信號就會產(chǎn)生失真(混疊),混疊是指采樣信號被還原成連續(xù)信號時(shí)產(chǎn)生彼此重疊而失真的現(xiàn)象,在理想濾波的情形下,濾掉高于奈氏頻率的信號成分即可防止混疊。
為了保證我們可以完美重建信號,我們需要將奈氏頻率以上的頻率分量全部濾除。抗混疊濾波就是做這個(gè)的。
③ 預(yù)處理
包括低通、高通、陷波等等,視需求而定。
低通 :一般用于濾除高頻分量和消除毛刺。
高通 :一般用于消除直流(DC)分量和緩慢漂移電位的影響。
陷波 :一般用于消除市電干擾(50、60Hz)。
但除了50Hz這種電源工頻干擾,還存在由其產(chǎn)生的整數(shù)倍的諧波干擾(100、150Hz等),文獻(xiàn)的作者提出:可以應(yīng)用boxcar smoothing kernel of size 1/50 Hz來解決。
PS:這個(gè)我也沒有見過,百度了一下好像是一種加矩形窗的函數(shù),效果就是在電源的各個(gè)諧波上都有零點(diǎn),從而真正消除電源干擾。
④ 數(shù)據(jù)分析
可能涉及帶通濾波(例如,隔離標(biāo)準(zhǔn)頻段,如'alpha''或''gamma'')或TF分析。
⑤ 展示
可能需要額外的平滑(也就是低通濾波),以去除毛刺/鋸齒。、
PS:這里我們先大致按以下方式理解一下低頻和高頻:低頻代表了整個(gè)信號的緩慢的變化趨勢,高頻代表了信號局部的劇烈變化。
好,我們接著往下講:
通俗來說,濾波器就是修改輸入信號的頻譜內(nèi)容的東西。
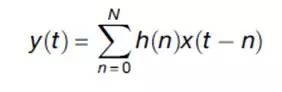
對于數(shù)字濾波器來說:t是分析時(shí)間點(diǎn),h(n)(n = 0,....,N)是沖激響應(yīng),上面這個(gè)方程就是卷積(也可以按滑動(dòng)平均來理解)。
沖激響應(yīng) (Impulseresponse,或者叫脈沖響應(yīng))就是某個(gè)線性時(shí)不變系統(tǒng)的輸入輸出關(guān)系的基本特征,它是由系統(tǒng)本身的性質(zhì)決定的,也就是在這個(gè)濾波器一出生時(shí)就定好了的!
沖激響應(yīng)這個(gè)概念比較重要,需要大家理解,以方便之后理解卷積。
線性時(shí)不變:線性和時(shí)不變,都是針對一個(gè)系統(tǒng)說的,這個(gè)系統(tǒng)可以是濾波器,也可以是別的等等。
①線性:指系統(tǒng)滿足疊加性和齊次性,疊加性指:當(dāng)多個(gè)輸入作用于系統(tǒng)時(shí),系統(tǒng)的輸出等于單個(gè)輸入的作用之和;
②齊次就是輸入放大n倍,輸出也放大n倍。
卷積 :輸出 = 輸入 * 系統(tǒng)(輸入與系統(tǒng)的沖激響應(yīng)做卷積,得到系統(tǒng)的輸出),同樣,這個(gè)系統(tǒng)可以是濾波器,也可以是別的什么東西。任一個(gè)線性系統(tǒng)的輸出都可以通過將輸入信號與系統(tǒng)函數(shù)(系統(tǒng)的沖激響應(yīng))做卷積獲得。
或者可以這么理解,
卷積是某一時(shí)刻的輸出是之前很多次輸入乘以各自的衰減系數(shù)之后的疊加而形成的,然后再把不同時(shí)刻的輸出點(diǎn)放在一起,形成一個(gè)函數(shù),這個(gè)函數(shù)就是輸出的函數(shù)。
在講述下面這張圖之前,先明確一個(gè)概念:因果性。
我們說,如果這個(gè)系統(tǒng)當(dāng)前時(shí)間點(diǎn)的輸出僅僅與當(dāng)前時(shí)間點(diǎn)及之前時(shí)間點(diǎn)的輸入有關(guān),那么我們說這個(gè)系統(tǒng)是因果的;反之,如果這個(gè)系統(tǒng)當(dāng)前時(shí)間點(diǎn)的輸出還與之后時(shí)間點(diǎn)的輸入有關(guān),那么我們說這個(gè)系統(tǒng)是非因果的。
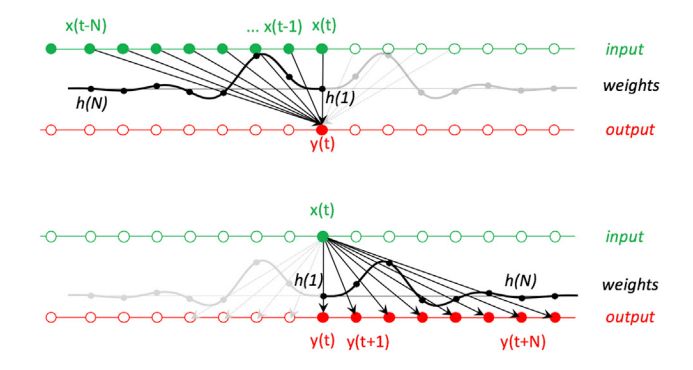
結(jié)合這張圖來理解卷積。這張圖基于的是因果系統(tǒng):綠線為輸入信號,它的時(shí)間序列是離散的;灰線為系統(tǒng)的沖激響應(yīng),是這個(gè)系統(tǒng)自身的特性;紅線為輸出。
上下兩部分講的是一個(gè)東西。咱們以上面的為例:輸出y的每個(gè)瞬時(shí)值是由沖激響應(yīng)h(n)加權(quán)后的輸入x的瞬時(shí)值之和。對于因果濾波器,僅輸入的過去或現(xiàn)在的瞬時(shí)值作出貢獻(xiàn)(對應(yīng)到h(n)的黑色部分)。對于非因果過濾器,未來的樣本也可以貢獻(xiàn)(對應(yīng)到h(n)的灰色部分)。
如果沒有理解,那么再來看下圖:描述卷積過程的另一種方式是輸入x的每個(gè)瞬時(shí)值影響輸出y的多個(gè)瞬時(shí)值,其影響的權(quán)重由沖激響應(yīng)h(n)確定。
而按照n的有限長或是無限長,我們又可將濾波器分為 FIR和IIR 。
**IIR(無限沖激響應(yīng))**由于其無限長的沖激響應(yīng),導(dǎo)致其幅頻特性精度很高,但其相位是非線性的,可以應(yīng)用于對相位信息不敏感的信號上;
**FIR(有限沖激響應(yīng))**的幅頻特性精度較之于IIR低,但是相位是線性的,所以不同頻率分量的信號經(jīng)過FIR濾波器后不發(fā)生相移。
我們再來說說濾波器的性能:性能取決于過渡帶的陡度,過渡帶的陡度取決于濾波器的類型和階數(shù)。過渡帶可以大致理解為:通帶與阻帶間的部分。
下圖為四種常見類型的濾波器:低通,高通,帶通和陷波。
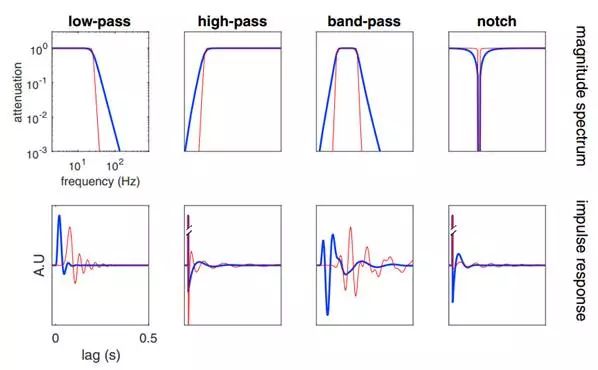
上半部分是幅度譜,下半部分是每個(gè)濾波器的沖激響應(yīng)。
對于每個(gè)濾波器,顯示了兩個(gè)版本,前三個(gè)的藍(lán)色為4階巴特沃斯濾波器,紅色為16階。第四個(gè)藍(lán)色為Q因子(中心頻率與帶寬的比率)為1(紅為10)的二階濾波器。
我們可以看到:階數(shù)越高,性能越好。同時(shí)在頻域中過渡帶越陡,在時(shí)域中沖激響應(yīng)越寬(時(shí)域擴(kuò)展-頻域壓縮)。
了解了以上這些,我們來看看濾波器是如何影響大腦數(shù)據(jù)的。
以下,我們將回顧在大腦活動(dòng)的時(shí)間序列中可能出現(xiàn)的一些典型“事件”,并了解它們?nèi)绾问艿匠S脼V波器的影響。
這個(gè)問題的答案取決于數(shù)據(jù)和濾波器。
1.脈沖或尖峰
在大腦的短暫的局部活動(dòng)中,其神經(jīng)元的“尖峰”活動(dòng)可以被建模為一個(gè)或幾個(gè)脈沖。
下圖為:濾波對短暫的局部事件(脈沖或尖峰)的影響。
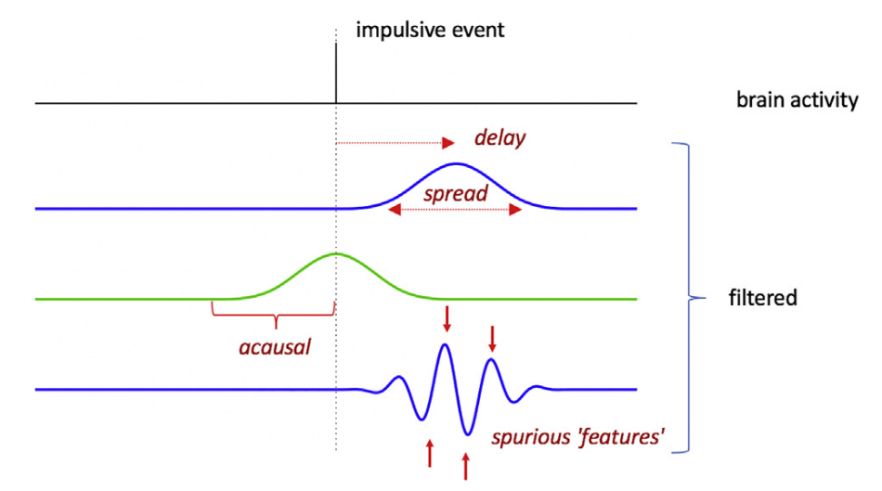
系統(tǒng)的響應(yīng)(輸入稱為激勵(lì),輸出是響應(yīng))隨時(shí)間擴(kuò)展(即,不再精確地在時(shí)間上定位)并且如果濾波器是因果關(guān)系則輸出會有延遲。如果濾波器是零相位(綠色),則消除整體延遲,但響應(yīng)是非因果的(即綠線所示)。
這種響應(yīng)可能包括由于濾波器振鈴效應(yīng)引起的多個(gè)偽特征。
什么是振鈴效應(yīng)?
振鈴效應(yīng) ,原指在圖像處理中,對一幅圖像進(jìn)行濾波處理時(shí),若選用的頻域?yàn)V波器具有陡峭的變化,則會使濾波圖像產(chǎn)生“振鈴”。
我們以理想低通濾波為例,其在時(shí)域上的表現(xiàn)為sinc函數(shù),對于辛格函數(shù)sinc而言,經(jīng)過傅里葉變換之后的函數(shù)形式為窗函數(shù)(理想低通濾波器在頻域上的形狀)形式,用圖像表示如下:
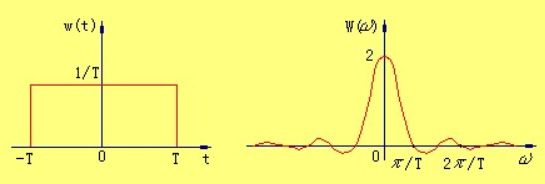
濾波,就是將系統(tǒng)與輸入在頻域相乘,轉(zhuǎn)換到在時(shí)域上就是卷積,由于受到sinc兩邊余波的影響,導(dǎo)致圖像出現(xiàn)振鈴現(xiàn)象(這里要理解卷積的概念,才能更好地理解振鈴現(xiàn)象)。
上述影響的性質(zhì)取決于濾波器,可以通過觀察其沖激響應(yīng)來判斷。
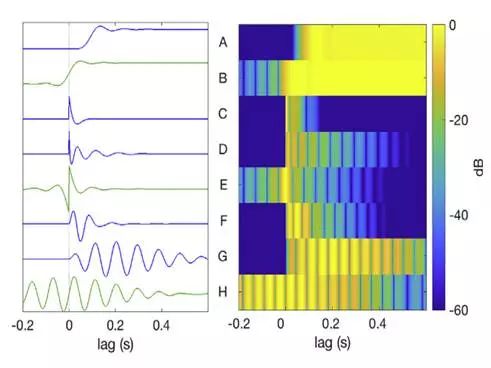
下圖為一系列常用濾波器的沖激響應(yīng)。
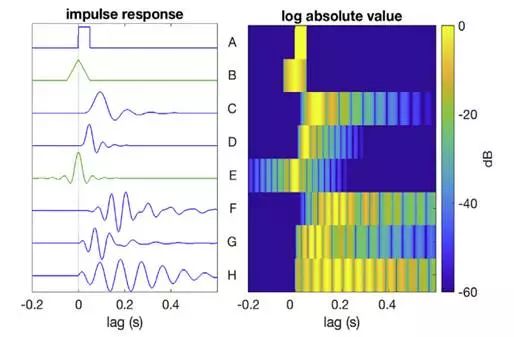
左圖為沖激響應(yīng)的時(shí)間序列,橫軸為持續(xù)時(shí)間lag(s);右圖顯示了其絕對值的對數(shù)(在60 dB處截?cái)?。綠色為非因果濾波器。
可見:高階濾波器時(shí)間跨度更大。帶通濾波器具有相對較長的脈沖響應(yīng),特別是當(dāng)帶寬較窄時(shí)。
但是真實(shí)的大腦事件與無限狹窄的單極脈沖不同,因?yàn)樗鼈兊膶挾仁怯邢薜模虼藢φ鎸?shí)大腦事件的反應(yīng)將與理想的脈沖響應(yīng)有所不同。在濾波器對大腦事件的響應(yīng)過程中,寬度大于事件特征寬度的沖激響應(yīng)是可以被識別的。同時(shí)較窄的特征可能出現(xiàn)平滑。
2.階躍
某些大腦事件可以被建模為階躍函數(shù)。下圖說明了濾波可以影響階躍式大腦事件的各種方式。可以平滑響應(yīng)(低通濾波器)和延遲響應(yīng)(因果濾波器)。
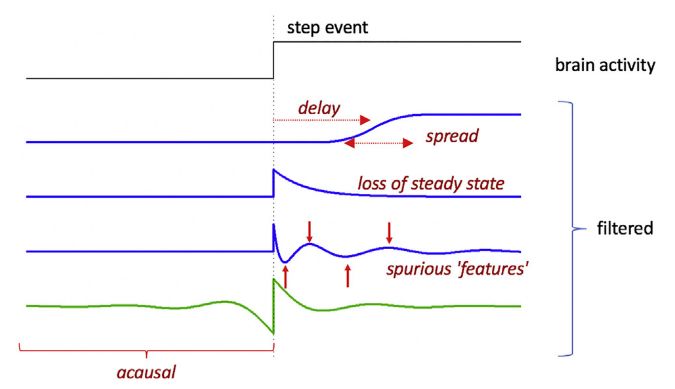
穩(wěn)態(tài)部分可能丟失(高通濾波器),并且可能出現(xiàn)虛假特征,其中一些可能發(fā)生在事件之前(非因果濾波器,綠色)。
這些影響的性質(zhì)還是取決于濾波器。可以從濾波器的階躍響應(yīng)(沖激響應(yīng)隨時(shí)間的積分)推斷出來。
A說明:濾波器為因果會造成事件延遲。
B說明:濾波器為非因果則會提前。
對于高通(C-E)或帶通(F-H)濾波器來說,穩(wěn)態(tài)部分會丟失。響應(yīng)可能包括虛假的偏移,如果濾波器是非因果性的,則其中一些出現(xiàn)在事件之前。(Filtfilt是用于設(shè)計(jì)非因果濾波器的函數(shù))。
響應(yīng)還可能是由振鈴效應(yīng)引起的振蕩(F-H)。
但是實(shí)際的階躍式大腦活動(dòng)與理想的階躍是不同的。在輸出中,可以識別出比事件開始時(shí)的階躍響應(yīng)更寬的階躍響應(yīng),而較窄的會變得平滑。
需要注意的是,穩(wěn)態(tài)部分的偏移會導(dǎo)致相反極性的階躍響應(yīng)。
3.振蕩活動(dòng)
大腦中的一些活動(dòng)是振蕩的。這種振蕩活動(dòng)可以被看作是正弦脈沖。
下圖為濾波對正弦脈沖的響應(yīng):一個(gè)脈沖的時(shí)間序列受到濾波的影響:它會隨著時(shí)間的推移而平滑和擴(kuò)散,如果濾波是因果的,它可能會延遲,如果濾波是非因果的,它可能會比事件開始的更早。
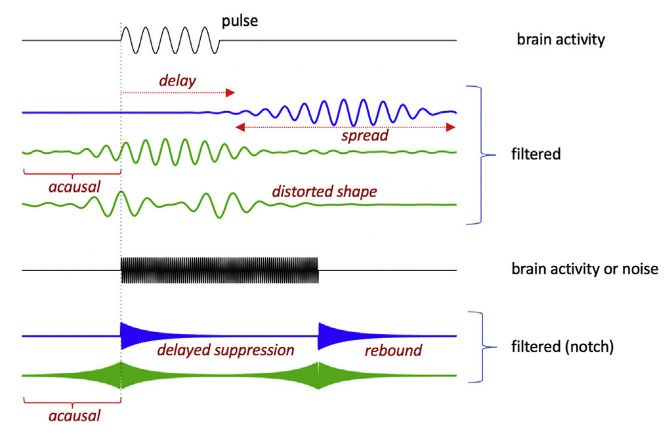
當(dāng)濾波器的通帶較窄時(shí)(人們可能想用它來增加這種振蕩活動(dòng)的信噪比),這種影響就更明顯。
對于調(diào)到脈沖頻率的陷波濾波器,這種抑制可能會延遲,而且在脈沖之后可能會有一個(gè)反彈的偽跡(振鈴效應(yīng))。非因果的話,該偽跡會在事件出現(xiàn)之前或之后出現(xiàn)。
濾波過程中會出現(xiàn)的問題:
1.有用信息的丟失和噪聲一起被抑制。
2.目標(biāo)的時(shí)間特征的失真:峰值或過渡帶可能被平滑,階躍可能變成脈沖,并且可能出現(xiàn)偽跡。
3.信號內(nèi)部特征之間或信號與外部事件(如刺激)之間的時(shí)間或因果關(guān)系模糊不清。
4.時(shí)頻(TF)分析
在時(shí)頻分析中,濾波器涉及的大多是比較底層的數(shù)據(jù)收集,從而影響最終的時(shí)頻分析圖。
時(shí)頻分析圖就是:在每個(gè)時(shí)間點(diǎn),分析產(chǎn)生一個(gè)頻譜,這些頻譜被連接起來形成二維的分析圖;或者我們可以將其等價(jià)為:在每個(gè)頻率使用一個(gè)濾波器。
下圖為:時(shí)頻分析引起的時(shí)間關(guān)系模糊
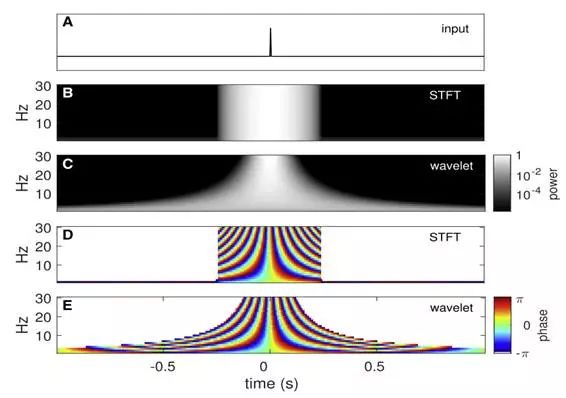
STFT頻譜圖中,對于所有頻率,分析窗口的大小是相同的。相反,在小波頻譜圖中,這個(gè)窗的大小隨頻率而變化,因?yàn)樾〔ㄗ儞Q的每個(gè)分析窗口跨越的周期的數(shù)量是相同的。
因此,結(jié)合前面的內(nèi)容,TF的結(jié)果要么相對于數(shù)據(jù)中的事件存在延遲(因果分析),要么在一定程度上反映了未來的事件(非因果分析)。
所以這種模糊的、非因果關(guān)系可能會誤導(dǎo)最終結(jié)論。
①報(bào)告完整的濾波器參數(shù)
比如說濾波器的類型、階數(shù)、頻率參數(shù),以及它是應(yīng)用于一個(gè)方向還是同時(shí)應(yīng)用于兩個(gè)方向的,還有沖激響應(yīng)(和/或階躍響應(yīng))的圖。
②使用低通時(shí),要確認(rèn):是否需要增強(qiáng)圖像的清晰度,或者是否要衰減高頻功率。
③若僅需要高通濾波器來消除恒定的DC偏移,則考慮采用減去整體均值的方法;如果還有一個(gè)緩慢的趨勢,請考慮“去趨勢”而不是高通濾波。
去趨勢引入了一個(gè)擬合函數(shù)(通過緩慢變化以適應(yīng)趨勢),將該函數(shù)擬合到數(shù)據(jù)然后減去引入的擬合函數(shù)。這種合適的擬合函數(shù)是一個(gè)低階多項(xiàng)式。
去趨勢與濾波一樣,去除趨勢對類似于毛刺的一類信號很敏感;但是這些可以通過“強(qiáng)有力的去趨勢”來解決。
④帶通濾波
盡量避免使用帶通濾波,因?yàn)闀碚疋徯?yīng)。即使為了提升信噪比而必須使用的話,也要選擇具有相對平坦的過渡帶和遠(yuǎn)離目標(biāo)頻段的截止頻率的濾波器。
⑤陷波
陷波濾波通常是為了抑制電源噪聲。同時(shí)作為濾波的替代方案,可以測量一個(gè)或多個(gè)參考通道上的電源噪聲并將其從數(shù)據(jù)中回歸。
如果高頻不感興趣,則可使用1/50 Hz的boxcar平滑內(nèi)核(一種加矩形窗的函數(shù))。這種簡單的低通濾波器在電源工頻及其所有諧波處都有零點(diǎn),從而可以完美消除電源噪聲及相關(guān)諧波干擾。
⑥時(shí)頻分析
如果感興趣的部分可以在時(shí)域中解釋,那么就可以避免TF分析。如果必須應(yīng)用TF分析,則考慮使用離散傅里葉變換來進(jìn)行分析,而不是小波分析。
若要使用小波分析,則應(yīng)使用相對較短的分析窗口來減少時(shí)間偏差,同時(shí)仔細(xì)考慮因果分析(有相位偏差但沒有因果關(guān)系問題)和非因果分析(無相位偏差但存在被誤認(rèn)為是因果關(guān)系的風(fēng)險(xiǎn))之間的選擇。
要做到以上這些,我們可能需要:
了解我們使用的濾波器;了解存在的噪聲;在源頭消滅噪聲(不太可能);確保擁有足夠的抗混疊;考慮濾波的替代方案;選擇正確的濾波器。
-
數(shù)字轉(zhuǎn)換器
+關(guān)注
關(guān)注
0文章
239瀏覽量
27992 -
SNR
+關(guān)注
關(guān)注
3文章
197瀏覽量
24844 -
陷波濾波器
+關(guān)注
關(guān)注
2文章
33瀏覽量
10240 -
巴特沃斯濾波器
+關(guān)注
關(guān)注
0文章
16瀏覽量
7408 -
高通濾波器
+關(guān)注
關(guān)注
0文章
99瀏覽量
11292
發(fā)布評論請先 登錄
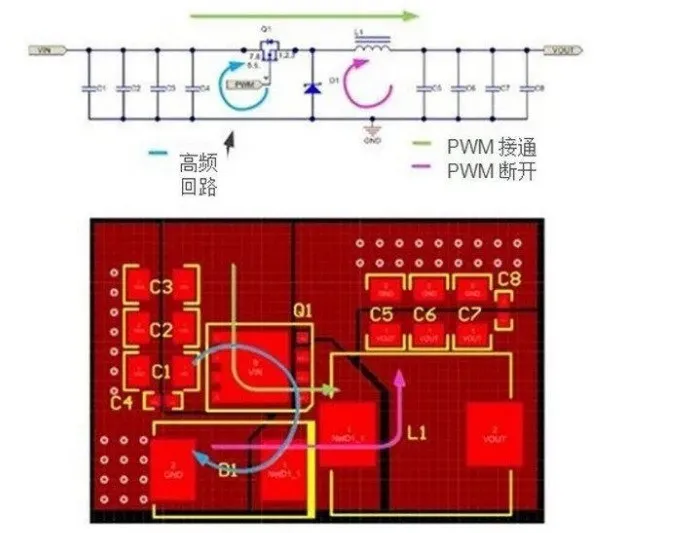
成功電源設(shè)計(jì),布局是其中最重要一個(gè)環(huán)節(jié)
數(shù)據(jù)處理
采集程序數(shù)據(jù)處理的時(shí)候數(shù)字濾波器就會報(bào)錯(cuò)
數(shù)據(jù)處理問題!
話題:寫下你認(rèn)為現(xiàn)存的宇宙中最本質(zhì)最重要的一條科學(xué)理論!
數(shù)據(jù)處理與控制策略
自適應(yīng)濾波在平臺自標(biāo)定數(shù)據(jù)處理中的應(yīng)用
基于Matlab的轉(zhuǎn)爐耳軸軸承狀態(tài)檢測數(shù)據(jù)處理程序的開發(fā)
Thumb數(shù)據(jù)處理指令
基于MCMC粒子濾波的GPS定位數(shù)據(jù)處理
電源布局是其中最重要的一個(gè)環(huán)節(jié)





 數(shù)據(jù)處理中最重要的濾波原理講解
數(shù)據(jù)處理中最重要的濾波原理講解











評論